人教版九年级数学上册同步精品讲义及试卷 第二十四章 圆单元检测（二）

第30课  圆单元检测（二）

一、单选题

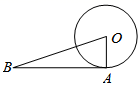
1．如图，AB是的切线，A切点，连接OA，OB，若，则的度数为（    ）

A．40° B．50° C．60° D．70°

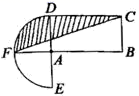
2．设计一个商标图案，如图所示，在矩形ABCD中，AB=2BC，且AB=8cm，以A为圆心、AD的长为半径作半圆，则商标图案(阴影部分)的面积等于（   ）

A．(4π+8)cm2 B．(4π+16)cm2 C．(3π+8)cm2 D．(3π+16)cm2

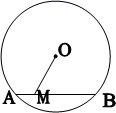
3．如图，⊙O的半径为5，弦的长为8，点在线段（包括端点）上移动，则的取值范围是（ ）

A． B． C． D．

4．如图所示，“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题，“今有圆材，埋在壁中，不知大小，以锯锯之，深两寸，锯道长八寸，问径几何？”用现代的数学语言表述是：“为的直径，弦，垂足为点，寸，寸，求直径的长？”依题意的长为（  ）

A．6寸 B．8寸 C．10寸 D．12寸

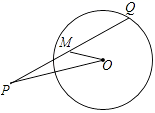
5．如图，已知P是⊙O外一点，Q是⊙O上的动点，线段PQ的中点为M，连接OP，OM．若⊙O的半径为2，OP=4，则线段OM的最小值是（　　）

A．0 B．1 C．2 D．3

6．一条弦把圆周分成两部分，则这条弦所对的圆周角为（       ）

A． B． C． D．或

7．如图，AB、AC是⊙O的切线，B、C为切点，∠A＝50°，点P是圆上异于B、C的点，则∠BPC的度数是（　　）

A．65° B．115° C．115°或65° D．130°或65°

二、填空题

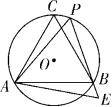
8．如图，的半径为5，为的内接三角形，且，点P在劣弧上运动（不与点C、B重合），连接并延长，在的延长线上取一点E，使得，则的最大值是________．

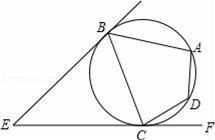
9．如图，EB，EC是⊙O的两条切线，与⊙O相切于B，C两点，点A，D在圆上．若∠E=46°，∠DCF=32°，则∠A的度数是____°．

10．已知⊙O1与⊙O2的半径、分别是方程 的两实根，若⊙O1与⊙O2的圆心距=5．则⊙O1与⊙O2的位置关系是           .

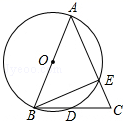
11．如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°，给出以下五个结论：①∠EBC=22.5°；②BD=DC；③AE=2EC；④劣弧是劣弧的2倍；⑤AE=BC，其中正确的序号是_________．

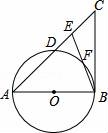
12．(2016广西省贺州市第25题)如图，在△ABC中，E是AC边上的一点，且AE=AB，∠BAC=2∠CBE，以AB为直径作⊙O交AC于点D，交BE于点F．

（1）求证：BC是⊙O的切线；

（2）若AB=8，BC=6，求DE的长．

13．两圆内切，其中一个圆的半径为5，两圆的圆心距为2，则另一个圆的半径是____．

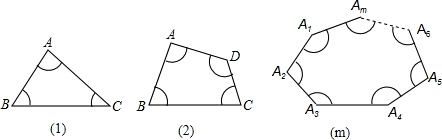
14．如图中（1）、（2）、…（m）分别是边长均大于2的三角形、四边形、…、凸n边形．分别以它们的各顶点为圆心，以1为半径画弧与两邻边相交，得到3条弧、4条弧…、n条弧．

（1）3条弧的弧长的和为_____；

（2）4条弧的弧长的和为_____；

（3）求图（m）中n条弧的弧长的和 （用n表示）．_____

三、解答题

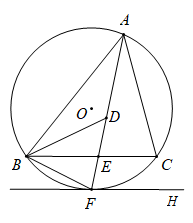
15．如图，⊙O是△ABC的外接圆，FH是⊙O 的切线，切点为F，FH∥BC，连结AF交BC于E，∠ABC的平分线BD交AF于D，连结BF．

（1）证明：AF平分∠BAC；

（2）证明：BF＝FD；

（3）若EF＝4，DE＝3，求AD的长．

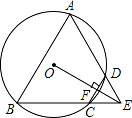
16．如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．

（1）求证：∠A=∠AEB；

（2）连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形．

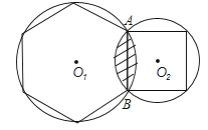
17．如图，相交两圆的公共弦AB长为120cm，它分别是一圆内接正六边形的边和另一圆内接正方形的边，求两圆相交弧间的阴影部分的面积．

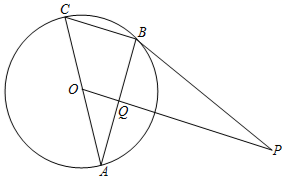
18．如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB，AB，∠PBA＝∠C．

（1）求证：PB是⊙O的切线；

（2）连接OP，交AB于点Q，若OP＝6，⊙O的半径为2，求PB的长．

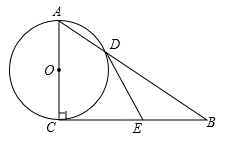
19．如图，已知的半径为1，是的直径，过点作的切线，是的中点，交于点．

（1）直接写出和的数量关系：__________；

（2）是的切线吗？若是，给出证明；若不是，说明理由；

（3）填空：当__________时，四边形是平行四边形，同时以点、、、为顶点的四边形是__________．

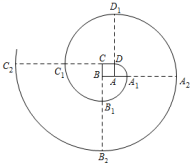
20．如图，四边形是正方形，曲线…是由一段段度的弧组成的．其中：的圆心为点，半径为；的圆心为点，半径为；在的圆心为点，半径为；的圆心为点，半径为；…，，，，…的圆心依次按点，，，循环．若正方形的边长为，求的长．