人教版九年级数学上册同步精品讲义及试卷 第27课 随机事件和概率

第27课  随机事件和概率

知识点01  必然事件、不可能事件和随机事件

1．必然事件

在一定条件下重复进行试验时，在每次试验中                的事件，叫做必然事件．

2．不可能事件

 在每次试验中都          的事件叫做不可能事件．

3．随机事件

在一定条件下，                    的事件，称为随机事件.

【注意】

(1)必然发生的事件和不可能发生的事件均为“          ”，随机事件又称为“          ”；

(2)要知道事件发生的可能性大小首先要确定事件是什么类型.

一般地，必然发生的事件发生的可能性最大，不可能发生的事件发生的可能性最小，随机事件发生的可能性有大有小，不同的随机事件发生的可能性的大小有可能不同.

知识点02  概率的意义

概率是从数量上刻画了一个随机事件发生的可能性的大小.一般地，在大量重复试验中，如果事件A发生的频率会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率(probability)，记为 .

【注意】

(1)概率是频率的          ，而频率是概率的          ；
(2)概率反映了随机事件发生的可能性的大小；
(3) 事件A的概率是一个          0，且          1的数，即          ，其中P(必然事件)=   ，P(不可能事件)=   ，0<P(随机事件)<1.

考法01   随机事件

【典例1】下列事件中，是随机事件的是（     ）

A．明天下雨 B．15个人中至少有两个人出生在同月

C．三角形内角和为180° D．太阳从西方升起

【典例2】下列事件为必然事件的是（       ）

A．一名射击运动员射击一次，中靶

B．彩票的中奖率是15%，那么买100张彩票必有15张中奖

C．掷一枚质地均匀的骰子，掷出的点数是质数

D．一个三角形，其任意两边之和大于第三边

【典例3】事件“任意抛掷一枚骰子，点数为3的面朝上”是（    ）

A．确定事件 B．随机事件 C．必然事件 D．不可能事件

【典例4】下列事件为确定事件的是（    ）

A．6张相同的小标签分别标有数字1～6，从中任意抽取一张，抽到5号签

B．抛掷1枚质地均匀的硬币反面朝上

C．篮球运动员投篮一次，命中篮筐

D．长度分别是3，4，5的三条线段能围成一个三角形

考法02   概率

【典例5】在一个不透明的袋中装有6个只有颜色不同的小球，其中3个红球、2个白球和1个黄球．从袋中任意摸出一个球，是红球的概率为（　　）

A． B． C． D．

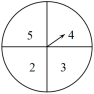
【典例6】如图是一个质地均匀的转盘，转盘中四个扇形的面积都相等，小明随意转动转盘1次，转盘停止转动后，指针指向的数字为偶数的概率为（若指针指在分割线上，需重新转动，直到指针指向某一扇形为止）（    ）

A． B． C． D．

【典例7】50瓶饮料中有2瓶已过了保质期．从该50瓶饮料中任取1瓶，取到已过保质期的饮料的概率是（    ）

A． B． C． D．

【典例8】五张卡片分别写着-3，-2，0，1，2数字，任意抽取一张是非负数的概率为（　　）

A． B． C． D．

题组A  基础过关练

1．下列事件中，属于必然事件的是（    ）

A．购买一张彩票，中奖 B．三角形的两边之和大于第三边 C．经过有交通信号灯的路口，遇到红灯 D．两个角相等，它们是对顶角

2．下列事件中，属于必然事件的是（　　）

A．春雨绵绵 B．春光明媚 C．春去夏来 D．春耕秋收

3．在一个不透明的口袋中装有3个白球和4个黄球这些球除颜色不同外其他完全相同，从袋子中随机摸出一个球，摸到白球的概率为（   ）

A． B． C． D．

4．小敏同学连续抛了两次硬币，都是正面朝上，那么他第三次抛硬币时，出现正面朝上的概率是（    ）

A．0 B．1 C． D．

5．下列语句描述的事件中，是随机事件的为（    ）

A．打草惊蛇，叶落归根 B．竹篮打水，水中捞月

C．瓜熟蒂落，水到渠成 D．心想事成，万事如意

6．下列事件：①期末测试中，1班优于2班；②等边三角形的三条高交于一点；③二元一次方程有无数个解；④长为的三条线段能围成一个三角形．其中确定事件有（   ）

A．1个 B．2个 C．3个 D．4个

7．小红通过一个设有红绿灯的十字路口时遇到绿灯，这是_______ 事件（填“随机”或“确定”）．

8．如果所示的地板由15块方砖组成，每一块方砖除颜色外完全相同，小球自由滚动，随机停在黑色方砖的概率为_________．

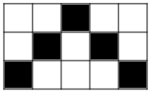
9．指出下列事件中，哪些是必然事件，哪些是不可能事件．

①两条平行线被第三条直线所截，同位角相等；

②367人中至少有2人的生日相同；

③没有水分，种子也会发芽；

④某运动员百米赛跑的成绩是；

⑤同种电荷相互排斥；

⑥通常情况下，高铁比普通列车快；

⑦用长度分别为3 cm，5 cm，8 cm的三条线段能围成一个三角形．

10．一个不透明的口袋中装有各色小球16只，其中5只红球、3只黑球、4只白球、4只绿球．求：

(1)从中取出一球为白球的概率．

(2)从中取出一球为红球或黑球的概率．

题组B  能力提升练

1．在做“抛一枚质地均匀的硬币”试验时，下列说法正确的是（   ）

A．随着抛掷次数的增加，反面向下的频率越来越大

B．当抛掷的次数很大时，正面向上的次数一定为

C．不同次数的试验，正面向上的频率可能会不相同

D．连续抛100次硬币都是正面向上，第101次抛掷出现正面向上的概率小于

2．如图所示，在三个挡板的后面各藏着一只动物，分别是小猫、小狗、小熊，小明和小刚各猜一次，只要能猜中哪个挡板后面是小猫便可获胜，则两人同时获胜的概率（    ）

A． B． C． D．

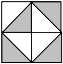
3．如图，是由8块相同的等腰直角三角形黑白瓷砖镶嵌而成的正方形地面示意图，一只蚂蚁在上面自由爬动，并随机停留在某块瓷砖上，蚂蚁停留在黑色瓷砖上的概率是（　　）

A． B． C． D．

4．下列事件中，是不确定事件的是（    ）

A．雨后有彩虹 B．内错角相等，两条直线平行

C．对顶角相等 D．三角形的内角和为180°

5．下列事件中，是随机事件的是（    ）

A．通常加热到时，水沸腾

B．随意翻到一本书的某页，这页的页码是偶数

C．任意画一个三角形，其内角和是

D．明天太阳从东方升起

6．下列成语或词语所描述的事件中，不可能发生的是（    ）

A．水中捞月 B．旭日东升 C．守株待兔 D．夕阳西下

7．小强投一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，则向上的一面的点数大于1且小于6的概率为 _____．

8．有五张背面完全相同的纸质卡片，其正面分别标有数：6、、、－2、．将它们背面朝上洗匀后，从中随机抽取一张卡片，则其正面的数是无理数的概率是________．

9．“十一”黄金周期间，某购物广场举办迎国庆有奖销售活动，每购物满100元，就会有一次转动大转盘的机会，某顾客获得一次转动大转盘的机会，请你根据大转盘来计算：

(1)该顾客享受七折优惠的概率；

(2)该顾客得10元现金奖的概率；

(3)该顾客中奖得现金的概率是多少？

10．为了加强新冠疫情的防控，某社区调查统计了A、B、C三栋居民楼全体居民的疫苗接种情况，得到如下统计表（不完整）：

(1)求变量y与变量x之间的关系式；

(2)若A、B、C三栋居民楼一共有居民150人，请直接写出x和y的值，并求下列事件发生的概率；

事件1：从C栋的居民中随机选择一人，该居民已经接种疫苗；

事件2：从A、B、C三栋的居民中随机选择人，该居民未接种疫苗．

题组C  培优拔尖练

1．从一副扑克牌中任意抽取1张，下列事件发生的可能性最大的是（    ）

A．这张牌是“A” B．这张牌是“大王”

C．这张牌是“黑桃” D．这张牌的点数是10

2．下列事件中，是必然事件的是（　　）

A．抛掷一枚硬币，反面朝上

B．打开电视，正在播放《美术经典中的党史》

C．任意画一个四边形，它的内角和等于

D．在一个只装有白球的口袋中摸出红球

3．下列说法正确的是（   ）

A．小明投篮投中的概率是0.6，说明他投10次篮球一定能中6次

B．为了解全国中学生的节水意识，应采用普查的方式

C．为了解某校300名九年级学生的睡眠时间，从中抽取50名九年级学生进行调查，在这个事件中，样本容量是300

D．一个不透明口袋中装有3个红球2个白球，除颜色外都相同，从中任意摸出一个球，摸到红球的可能性比白球大

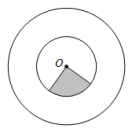
4．如图所示，镖盘为两个半径为1：2的两个同心圆，其中阴影部分为小圆内部一个的扇形，向大圆上投掷飞镖，则镖针落在阴影部分的概率为（     ）

A． B． C． D．

5．在一次数学活动课上，王老师将1～8共八个整数依次写在八张不透明的卡片上（每张卡片上只写一个数字，每一个数字只写在一张卡片上，而且把写有数字的那一面朝下）．他先像洗扑克牌一样打乱这些卡片的顺序，然后把甲、乙、丙、丁四位同学叫到讲台上，随机地发给每位同学两张卡片，并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上，写出的结果依次是：甲：12；乙：11；丙：9；丁：4，则拿到数字5的同学是（    ）

A．甲 B．乙 C．丙 D．丁

6．如图，A、B是边长为1的小正方形组成的网格上的两个格点，在其余的格点中任意放置点C，恰好能使△ABC构成等腰三角形的概率是（    ）

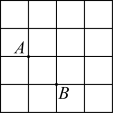
A． B． C． D．

7．如图，数学活动小组自制了一个飞镖盘．若向飞镖盘内投掷飞镖（落在边界线重新投掷），则飞镖落在阴影区域的概率是_____．

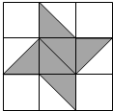
8．在不透明的袋子中装有北京冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”的纪念卡片12张，每张卡片除吉祥物外其他完全相同，从中任意拿出一张，拿到“冰墩墩”纪念卡片的概率为P1，拿到“雪容融”纪念卡片的概率为P2，且P1﹣P2＝0.5，那么袋子中“冰墩墩”纪念卡片的张数是 _____．

9．新世纪商场举行有奖销售，发行奖券5万张，其中设一等奖3个，二等奖10个，三等奖50个，四等奖200个，五等奖1000个．

(1)获得一、二等奖的概率是多少？

(2)获奖的概率是多少？

10．某可乐公司利用周末搞促销活动：每购买一瓶可乐，便可参加摇奖一次，摇奖牌是平均分成8个扇形的转盘，如图所示．

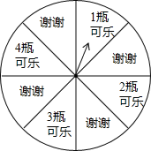
(1)中奖的概率是多少？

(2)中奖得4瓶可乐的概率是多少？

(3)如果促销活动当天能卖出可乐1000瓶，那么该促销点当天应准备奖品可乐多少瓶？

(4)已知一瓶可乐的成本是1元，售价是2元，摊位费每天100元，在周末两天的促销活动中，每天能卖出可乐1000瓶，公司是赔钱还是赚钱？金额是多少？