






还剩13页未读,
继续阅读
所属成套资源:2023新版华东师大版八年级数学上册全一册作业课件
成套系列资料,整套一键下载
2023八年级数学上册第12章整式的乘除全章综合检测作业课件新版华东师大版
展开
这是一份2023八年级数学上册第12章整式的乘除全章综合检测作业课件新版华东师大版,共21页。
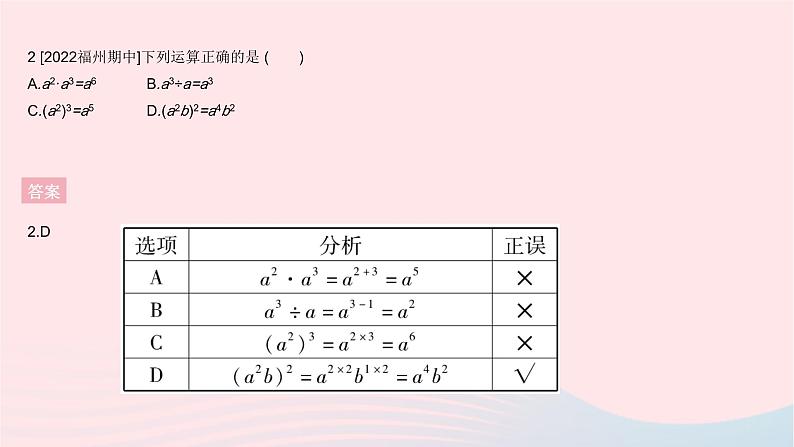
全章综合检测一、选择题1. [2020兰州中考A卷]化简:a(a-2)+4a=( )A.a2+2a B.a2+6aC.a2-6a D.a2+4a-2答案1.A a(a-2)+4a=a2-2a+4a=a2+2a.2 [2022福州期中]下列运算正确的是 ( )A.a2·a3=a6 B.a3÷a=a3C.(a2)3=a5 D.(a2b)2=a4b2答案2.D3. 某电子计算机每秒可进行4×109次运算,则2×102秒可进行运算的次数为 ( )A.8×1011 B.8×1018C.6×1011 D.6×1018答案3.A (4×109)×(2×102)=8×1011.4. 选择计算(-4xy2+3x2y)·(4xy2+3x2y)的最佳方法是 ( )A.运用多项式乘多项式法则B.运用平方差公式C.运用单项式乘多项式法则D.运用完全平方公式答案4.B 答案 答案6.B 答案 8. 已知三个实数a,b,c满足a-2b+c=0,a+2b+c<0,则 ( )A.b>0,b2-ac≤0 B.b<0,b2-ac≤0C.b>0,b2-ac≥0 D.b<0,b2-ac≥0答案 二、填空题9. 计算:(-m3)2÷m4= . 答案9.m2 (-m3)2÷m4=m6÷m4=m2. 答案 11. 若2x-3y+z-2=0,则16x÷82y×4z的值为 . 答案11.16 16x÷82y×4z=(24)x÷(23)2y×(22)z=24x÷26y×22z=22(2x-3y+z).∵2x-3y+z-2=0,∴2x-3y+z=2,∴原式=24=16.12. [2022营口期末]如图有两张正方形纸片A和B,图1将B放置在A内部,测得阴影部分的面积为2,图2将正方形A,B并列放置后构造新正方形,测得阴影部分的面积为20,若将3个正方形A和2个正方形B并列放置后构造的新正方形如图3(图2,图3中正方形A,B纸片均无重叠部分),则图3中阴影部分的面积为 . 答案12.42 设正方形纸片A的边长为a,正方形纸片B的边长为b,则题图1中阴影部分的面积为a2-b2=2,题图2中阴影部分的面积为(a+b)2-a2-b2=a2+2ab+b2-a2-b2=2ab=20,所以ab=10,所以题图3中阴影部分的面积为(2a+b)2-3a2-2b2=a2-b2+4ab=2+4×10=42. 答案 14. 分解因式.(1)-2x2+4xy-2y2; (2)x4-81y4.答案14.解:(1)-2x2+4xy-2y2=-2(x2-2xy+y2)=-2(x-y)2.(2)x4-81y4=(x2)2-(9y2)2=(x2+9y2)(x2-9y2)=(x2+9y2)[x2-(3y)2]=(x2+9y2)(x+3y)(x-3y). 答案15.解:(1)根据题意得m-1=0且n+2=0,解得m=1,n=-2.(2)m(m-3n)+(m+2n)2-4n2=m2-3mn+m2+4mn+4n2-4n2=2m2+mn=m(2m+n),当m=1,n=-2时,原式=1×(2×1-2)=0.16. 新情境[2022淮安期中]有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和-16,如图所示.如,第一次按键后,A,B两区分别显示:(1)从初始状态按2次后,分别求A,B两区显示的结果;(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能否为负数,说明理由.答案16.解:(1)A区显示的结果为25+a2+a2=25+2a2,B区显示的结果为-16-3a-3a=-16-6a.(2)从初始状态按4次后,A区显示的结果为25+4a2,B区显示的结果为-16-12a,它们的和为(5+4a2)+(-16-12a)=25+4a2-16-12a=4a2-12a+9.这个和不能为负数.理由:∵4a2-12a+9=(2a)2-2×(2a)×3+32=(2a-3)2≥0,∴A,B两区代数式的和不能为负数.17. 先阅读材料,再解答下列问题:材料:分解因式(x+y)2+2(x+y)+1.解:令x+y=A,则(x+y)2+2(x+y)+1=A2+2A+1=(A+1)2,故(x+y)2+2(x+y)+1=(x+y+1)2.上述解题过程用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法,请你解答下列问题:(1)分解因式:1+2(x-y)+(x-y)2= . (2)分解因式:(a+b)(a+b-4)+4.(3)试说明:若n为整数,则式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.答案17.解:(1)(x-y+1)2(2)令a+b=A,则(a+b)(a+b-4)+4=A(A-4)+4=A2-4A+4=(A-2)2,故(a+b)(a+b-4)+4=(a+b-2)2.(3)(n+1)(n+2)(n2+3n)+1=(n2+3n+2)(n2+3n)+1=(n2+3n)2+2(n2+3n)+1=(n2+3n+1)2.∵n为整数,∴n2+3n+1也为整数,∴式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.
全章综合检测一、选择题1. [2020兰州中考A卷]化简:a(a-2)+4a=( )A.a2+2a B.a2+6aC.a2-6a D.a2+4a-2答案1.A a(a-2)+4a=a2-2a+4a=a2+2a.2 [2022福州期中]下列运算正确的是 ( )A.a2·a3=a6 B.a3÷a=a3C.(a2)3=a5 D.(a2b)2=a4b2答案2.D3. 某电子计算机每秒可进行4×109次运算,则2×102秒可进行运算的次数为 ( )A.8×1011 B.8×1018C.6×1011 D.6×1018答案3.A (4×109)×(2×102)=8×1011.4. 选择计算(-4xy2+3x2y)·(4xy2+3x2y)的最佳方法是 ( )A.运用多项式乘多项式法则B.运用平方差公式C.运用单项式乘多项式法则D.运用完全平方公式答案4.B 答案 答案6.B 答案 8. 已知三个实数a,b,c满足a-2b+c=0,a+2b+c<0,则 ( )A.b>0,b2-ac≤0 B.b<0,b2-ac≤0C.b>0,b2-ac≥0 D.b<0,b2-ac≥0答案 二、填空题9. 计算:(-m3)2÷m4= . 答案9.m2 (-m3)2÷m4=m6÷m4=m2. 答案 11. 若2x-3y+z-2=0,则16x÷82y×4z的值为 . 答案11.16 16x÷82y×4z=(24)x÷(23)2y×(22)z=24x÷26y×22z=22(2x-3y+z).∵2x-3y+z-2=0,∴2x-3y+z=2,∴原式=24=16.12. [2022营口期末]如图有两张正方形纸片A和B,图1将B放置在A内部,测得阴影部分的面积为2,图2将正方形A,B并列放置后构造新正方形,测得阴影部分的面积为20,若将3个正方形A和2个正方形B并列放置后构造的新正方形如图3(图2,图3中正方形A,B纸片均无重叠部分),则图3中阴影部分的面积为 . 答案12.42 设正方形纸片A的边长为a,正方形纸片B的边长为b,则题图1中阴影部分的面积为a2-b2=2,题图2中阴影部分的面积为(a+b)2-a2-b2=a2+2ab+b2-a2-b2=2ab=20,所以ab=10,所以题图3中阴影部分的面积为(2a+b)2-3a2-2b2=a2-b2+4ab=2+4×10=42. 答案 14. 分解因式.(1)-2x2+4xy-2y2; (2)x4-81y4.答案14.解:(1)-2x2+4xy-2y2=-2(x2-2xy+y2)=-2(x-y)2.(2)x4-81y4=(x2)2-(9y2)2=(x2+9y2)(x2-9y2)=(x2+9y2)[x2-(3y)2]=(x2+9y2)(x+3y)(x-3y). 答案15.解:(1)根据题意得m-1=0且n+2=0,解得m=1,n=-2.(2)m(m-3n)+(m+2n)2-4n2=m2-3mn+m2+4mn+4n2-4n2=2m2+mn=m(2m+n),当m=1,n=-2时,原式=1×(2×1-2)=0.16. 新情境[2022淮安期中]有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和-16,如图所示.如,第一次按键后,A,B两区分别显示:(1)从初始状态按2次后,分别求A,B两区显示的结果;(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能否为负数,说明理由.答案16.解:(1)A区显示的结果为25+a2+a2=25+2a2,B区显示的结果为-16-3a-3a=-16-6a.(2)从初始状态按4次后,A区显示的结果为25+4a2,B区显示的结果为-16-12a,它们的和为(5+4a2)+(-16-12a)=25+4a2-16-12a=4a2-12a+9.这个和不能为负数.理由:∵4a2-12a+9=(2a)2-2×(2a)×3+32=(2a-3)2≥0,∴A,B两区代数式的和不能为负数.17. 先阅读材料,再解答下列问题:材料:分解因式(x+y)2+2(x+y)+1.解:令x+y=A,则(x+y)2+2(x+y)+1=A2+2A+1=(A+1)2,故(x+y)2+2(x+y)+1=(x+y+1)2.上述解题过程用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法,请你解答下列问题:(1)分解因式:1+2(x-y)+(x-y)2= . (2)分解因式:(a+b)(a+b-4)+4.(3)试说明:若n为整数,则式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.答案17.解:(1)(x-y+1)2(2)令a+b=A,则(a+b)(a+b-4)+4=A(A-4)+4=A2-4A+4=(A-2)2,故(a+b)(a+b-4)+4=(a+b-2)2.(3)(n+1)(n+2)(n2+3n)+1=(n2+3n+2)(n2+3n)+1=(n2+3n)2+2(n2+3n)+1=(n2+3n+1)2.∵n为整数,∴n2+3n+1也为整数,∴式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.
相关资料
更多









