初中数学华师大版八年级上册3 边角边作业课件ppt

这是一份初中数学华师大版八年级上册3 边角边作业课件ppt，共21页。PPT课件主要包含了ACBD等内容，欢迎下载使用。
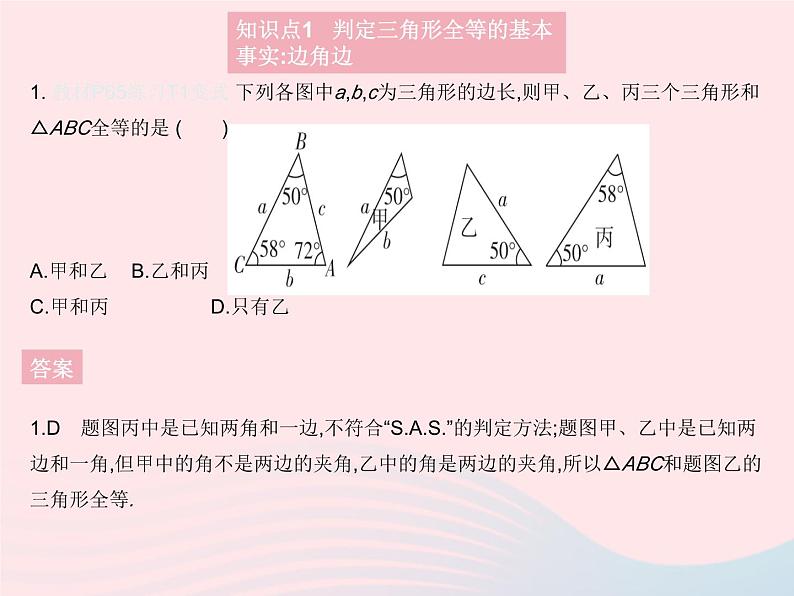
1. 教材P65练习T1变式 下列各图中a,b,c为三角形的边长,则甲、乙、丙三个三角形和△ABC全等的是 (　　)A.甲和乙 B.乙和丙C.甲和丙 D.只有乙
知识点1 判定三角形全等的基本事实:边角边
1.D　题图丙中是已知两角和一边,不符合“”的判定方法;题图甲、乙中是已知两边和一角,但甲中的角不是两边的夹角,乙中的角是两边的夹角,所以△ABC和题图乙的三角形全等.
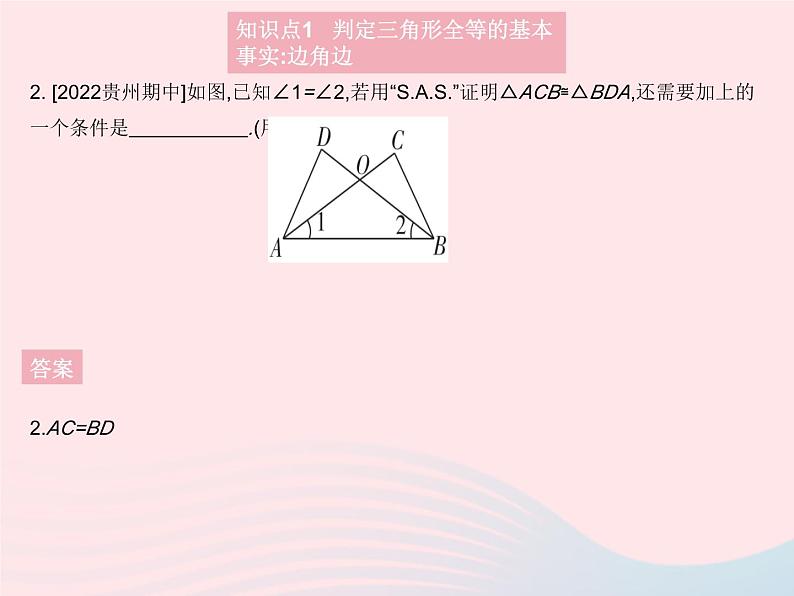
2. [2022贵州期中]如图,已知∠1=∠2,若用“”证明△ACB≌△BDA,还需要加上的一个条件是　　　　　　.(用图中字母表示) 
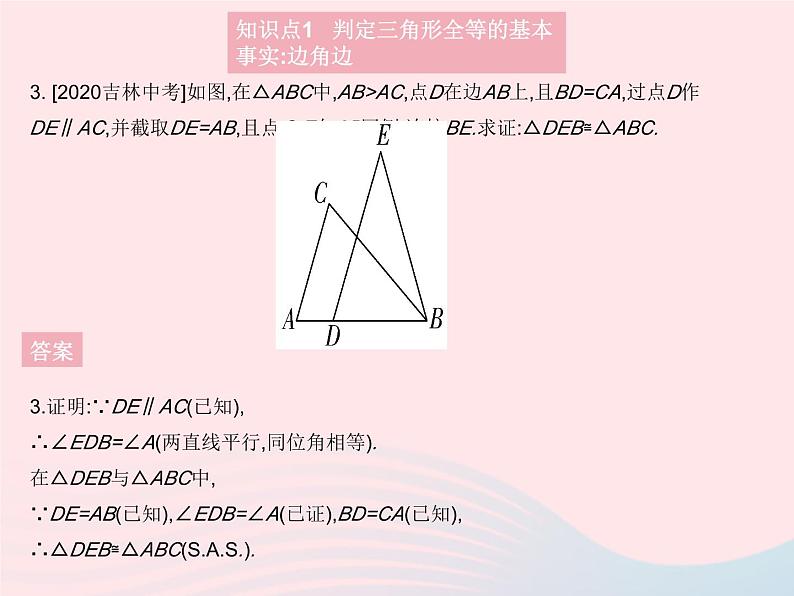
3. [2020吉林中考]如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
3.证明:∵DE∥AC(已知),∴∠EDB=∠A(两直线平行,同位角相等).在△DEB与△ABC中,∵DE=AB(已知),∠EDB=∠A(已证),BD=CA(已知),∴△DEB≌△ABC().
4. [2021宜宾中考]如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
4.证明:∵∠AOC=∠BOD(已知),∴∠AOC-∠AOD=∠BOD-∠AOD,∴∠COD=∠AOB(等式的性质).在△AOB和△COD中,∵OA=OC(已知),∠AOB=∠COD(已证),OB=OD(已知),∴△AOB≌△COD().
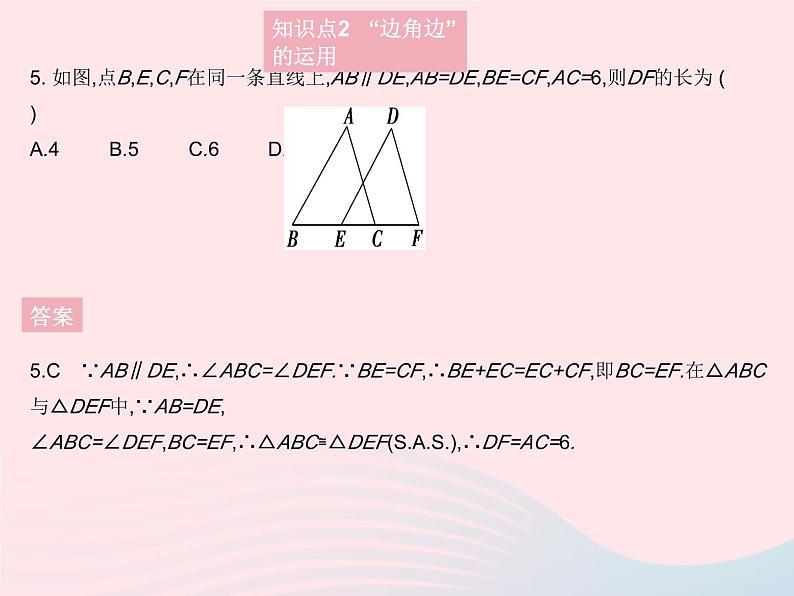
5. 如图,点B,E,C,F在同一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF的长为 (　　)A.4B.5C.6D.7
知识点2 “边角边”的运用
5.C　∵AB∥DE,∴∠ABC=∠DEF.∵BE=CF,∴BE+EC=EC+CF,即BC=EF.在△ABC与△DEF中,∵AB=DE,∠ABC=∠DEF,BC=EF,∴△ABC≌△DEF(),∴DF=AC=6.
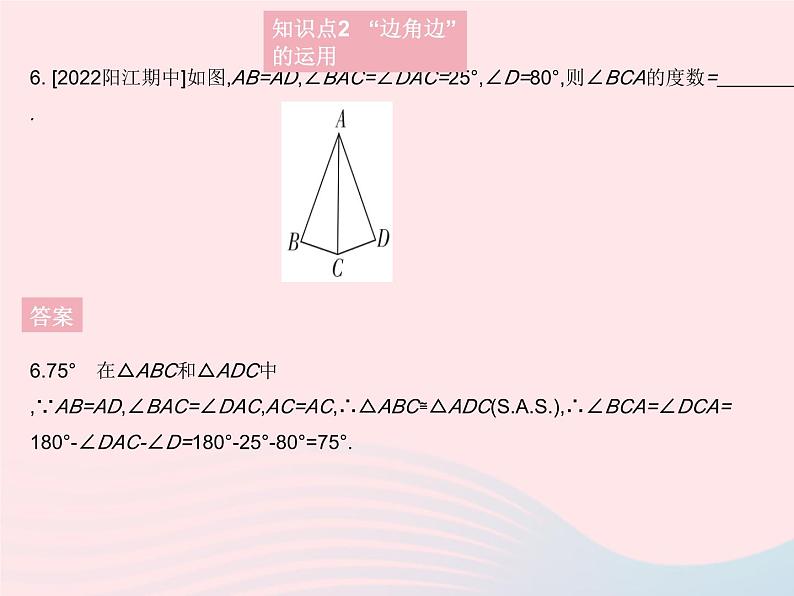
6. [2022阳江期中]如图,AB=AD,∠BAC=∠DAC=25°,∠D=80°,则∠BCA的度数=　　　　. 
6.75°　在△ABC和△ADC中,∵AB=AD,∠BAC=∠DAC,AC=AC,∴△ABC≌△ADC(),∴∠BCA=∠DCA=180°-∠DAC-∠D=180°-25°-80°=75°.
7. [2022十堰期中]某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35 cm.由以上信息你能求出CB的长度吗?并说明理由.
7.解:能.理由如下:∵O是AB,CD的中点(已知),∴OA=OB,OC=OD(中点的定义).在△AOD和△BOC中,∵OA=OB(已证),∠AOD=∠BOC(对顶角相等),OD=OC(已证),∴△AOD≌△BOC(),∴CB=AD(全等三角形的对应边相等).∵AD=35 cm,∴CB=35 cm.
1. [2022海东期中]如图,△ABC中,∠B=∠C=65°,BD=CE,BE=CF,则∠DEF的度数是(　　)A.75°B.70°C.65°D.60°
1.C　∵BD=CE,∠B=∠C=65°,BE=CF,∴△DBE≌△ECF(),∴∠BDE=∠CEF.∵∠BDE+∠BED=180°-65°=115°,∴∠BED+∠CEF=115°,∴∠DEF=180°-115°=65°.
2. [2022福州期中]如图,在孔雀开屏般漂亮的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7= (　　)A.312°B.315°C.317°D.320°
2.B　根据题意得,BL=EA,∠LBA=∠E,BA=EF,所以△LBA≌△AEF(),所以∠7=∠EAF.因为∠E=90°,所以∠EAF+∠1=90°,所以∠1+∠7=90°.同理可得∠2+∠6=90°,∠3+∠5=90°,易知∠4=45°,所以∠1+∠2+∠3+∠4+∠5+∠6+∠7=90°+90°+90°+45°=315°.
3. 易错题如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB→ BC→ CD→ DA向终点A运动.设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为　　　　. 
3.3或7　分两种情况讨论:①当BP=CE时,在△ABP与△DCE中,∵AB=DC,∠ABP=∠DCE=90°,BP=CE,∴△ABP≌△DCE,由题意得BP=t-2=1,∴t=3;②当AP=CE时,在△ABP与△CDE中,∵AB=CD,∠BAP=∠DCE=90°,AP=CE,∴△ABP≌△CDE,由题意得AP=8-t=1,解得t=7.综上,当t的值为3或7时,△ABP和△DCE全等.
4. [2021咸宁一模]如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM与BN交于点P.(1)求证:△ABM≌△BCN.(2)求∠APN的度数.
5. 新考法如图,公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB,CD,BC三段路上各有一只石凳E,F,M,且BE=CF,M是BC的中点,试说明三只石凳E,F,M恰好在一条直线上.(提示:通过证明∠EMF=180°来求解)
素养提升6 [2022荆州期中]某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.(1)如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,求证:△ACD≌△EBD.(2)如图2,EP是△DEF的中线.若EF=5,DE=3,则EP的取值范围是　　　　　. (3)如图3,AD是△ABC的中线,E,F分别在AB,AC上,且DE⊥DF.求证:BE+CF>EF.
6.(1)证明:∵AD是△ABC的中线,∴CD=BD.在△ACD和△EBD中,∵CD=BD,∠ADC=∠EDB,AD=ED,∴△ACD≌△EBD().(2)解:1