初中数学华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定1 全等三角形作业课件ppt

这是一份初中数学华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定1 全等三角形作业课件ppt，共23页。

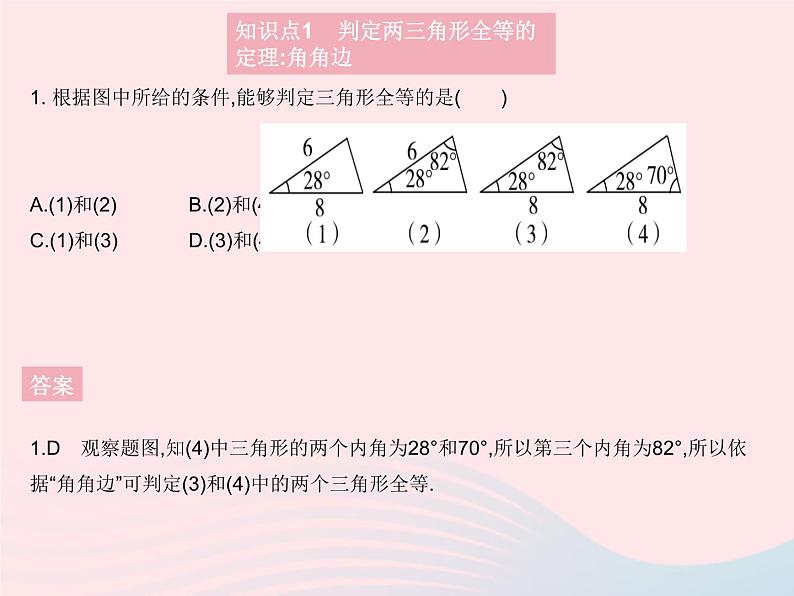
1. 根据图中所给的条件,能够判定三角形全等的是(　　)A.(1)和(2)B.(2)和(4)C.(1)和(3)D.(3)和(4)
知识点1 判定两三角形全等的定理:角角边
1.D　观察题图,知(4)中三角形的两个内角为28°和70°,所以第三个内角为82°,所以依据“角角边”可判定(3)和(4)中的两个三角形全等.
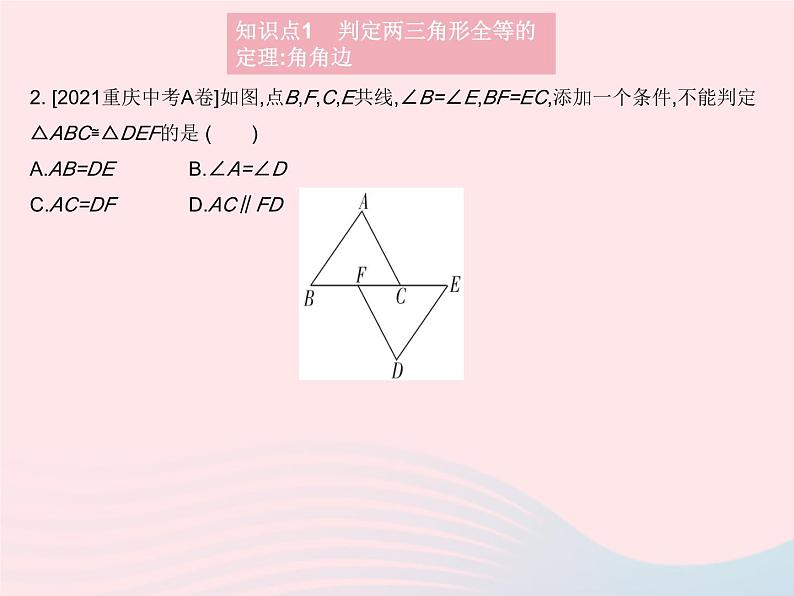
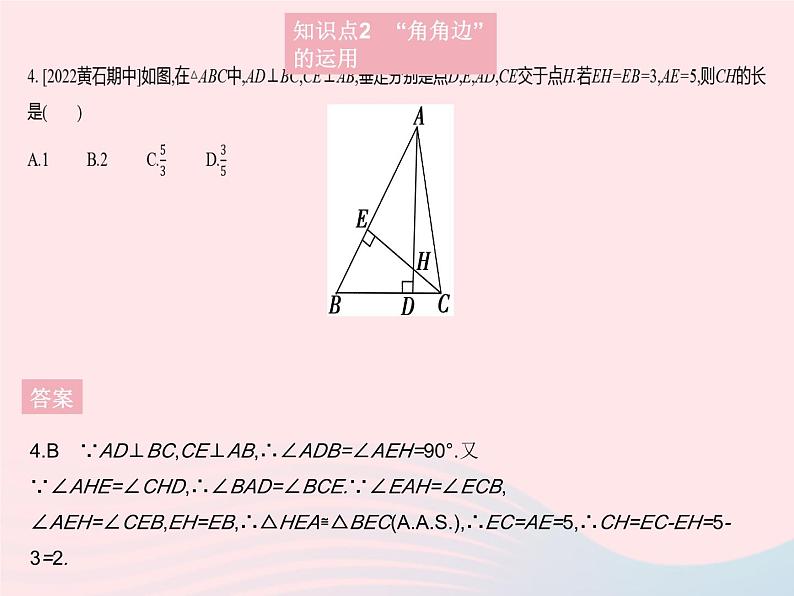
2. [2021重庆中考A卷]如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判定△ABC≌△DEF的是 (　　)A.AB=DEB.∠A=∠DC.AC=DFD.AC∥FD
2.C　已知BF=EC,所以BF +FC=EC+FC,即BC=EF.
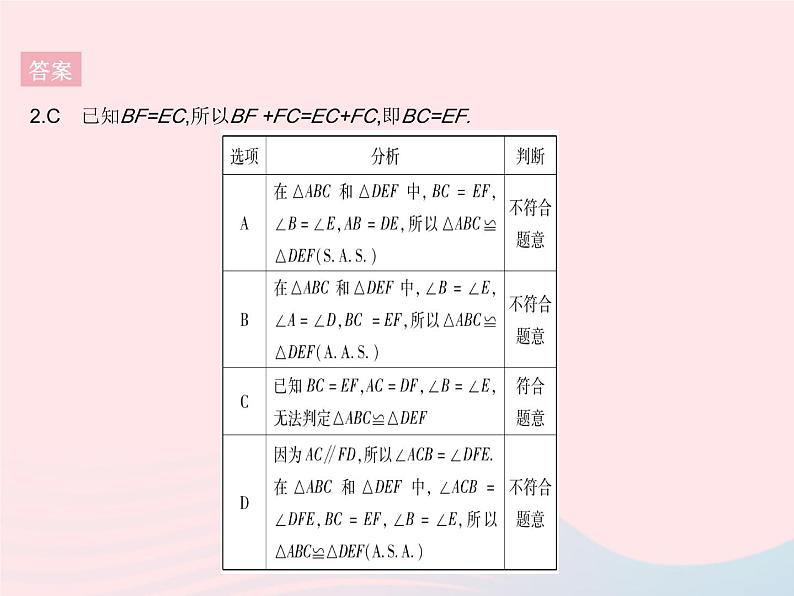
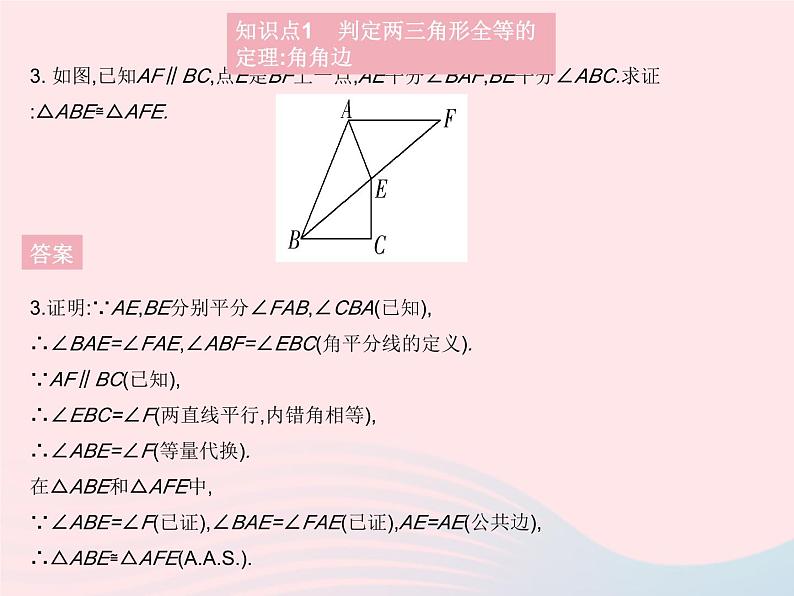
3. 如图,已知AF∥BC,点E是BF上一点,AE平分∠BAF,BE平分∠ABC.求证:△ABE≌△AFE.
3.证明:∵AE,BE分别平分∠FAB,∠CBA(已知),∴∠BAE=∠FAE,∠ABF=∠EBC(角平分线的定义).∵AF∥BC(已知),∴∠EBC=∠F(两直线平行,内错角相等),∴∠ABE=∠F(等量代换).在△ABE和△AFE中,∵∠ABE=∠F(已证),∠BAE=∠FAE(已证),AE=AE(公共边), ∴△ABE≌△AFE().
知识点2 “角角边”的运用
4.B　∵AD⊥BC,CE⊥AB,∴∠ADB=∠AEH=90°.又∵∠AHE=∠CHD,∴∠BAD=∠BCE.∵∠EAH=∠ECB,∠AEH=∠CEB,EH=EB,∴△HEA≌△BEC(),∴EC=AE=5,∴CH=EC-EH=5-3=2.
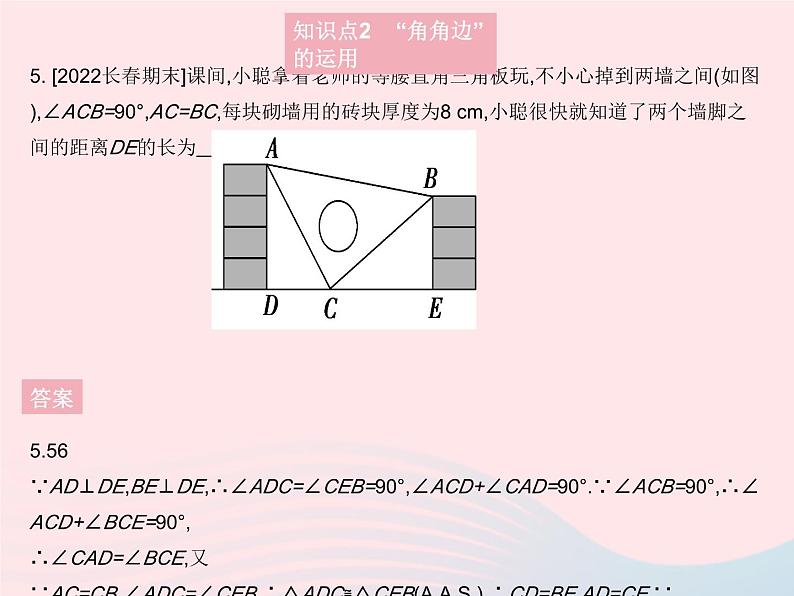
5. [2022长春期末]课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),∠ACB=90°,AC=BC,每块砌墙用的砖块厚度为8 cm,小聪很快就知道了两个墙脚之间的距离DE的长为　　　　　cm. 
5.56 ∵AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∠ACD+∠CAD=90°.∵∠ACB=90°,∴∠ACD+∠BCE=90°,∴∠CAD=∠BCE,又∵AC=CB,∠ADC=∠CEB,∴△ADC≌△CEB(),∴CD=BE,AD=CE.∵DE=CD+CE,∴DE=BE+AD=24+32=56(cm),∴两个墙脚之间的距离DE的长为56 cm.
6. 条件开放[2021铜仁中考]如图,AB交CD于点O,在△AOC与△BOD中,有下列三个条件:①OC=OD,②AC=BD,③∠A=∠B.请你在上述三个条件中选择两个为条件,另一个能作为这两个条件推出来的结论,并证明你的结论.(只要求写出一种正确的选法)(1)你选的条件为　　　　、　　　　,结论为　　　　. (2)证明你的结论.
6.(1)解:①　③　②(答案不唯一)(2)证明:在△AOC和△BOD中,∵∠A=∠B,∠AOC=∠BOD,OC=OD,∴△AOC≌△BOD (),∴AC=BD.
7. [2021金华二模]如图,在四边形ABCD中,∠ABC=90°,AD∥BC,以B为圆心、BC长为半径画弧,与AD相交于点E,连接BE,过点C作CF⊥BE,垂足为F.若AE=8,BC=10,求EF的长.
1. [2021秦皇岛期末]如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=4,BF=3,EF=2,则AD的长为 (　　)A.3B.5C.6D.7
1.B　∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠AFB=∠CED=90°,易得∠A=∠C.∵∠A=∠C,∠AFB=∠CED,AB=CD,∴△ABF≌△CDE(),∴AF=CE=4,DE=BF=3.∵EF=2,∴AD=AF+DF=AF+(DE-EF)=4+(3-2)=5.
2. 如图,已知△AEB和△AFC,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中一定正确的有 (　　)A.4个B.3个C.2个D.1个
2.B　在△ABE和△ACF中,∵∠E=∠F=90°,∠B=∠C,AE=AF,∴△ABE≌△ACF(),∴BE=CF,∠BAE=∠CAF,∴∠CAF-∠BAC=∠BAE-∠BAC,∴∠1=∠2.∵△ABE≌△ACF,∴AB=AC,又∵∠NAC=∠MAB,∠C=∠B,∴△ACN≌△ABM().由题中条件不能证明CD=DN.
3. [2022芜湖期末]小朋友荡秋千的画面如图1所示,其侧面示意图如图2所示,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5 m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5 m,点A到地面的距离AE=1.5 m,当他从A处摆动到A'处时,若A'B⊥AB于点B,则点A'到BD的距离为　　　　m. 
4. [2022长春期中]如图,点B,F,C,E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于点O.求证:AD与BE互相平分.
4.证明:∵FB=CE,∴BC=EF.∵AB∥ED,AC∥FD,∴∠ABC=∠DEF,∠ACB=∠DFE.在△ABC和△DEF中,∵∠ABC=∠DEF,BC=EF,∠ACB=∠DFE,∴△ABC≌△DEF(),∴AB=DE.在△AOB和△DOE中,∵∠AOB=∠DOE, ∠ABO=∠DEO,AB=DE, ∴△AOB≌△DOE(),∴OA=OD,OB=OE,∴AD与BE互相平分.
一图多变 “角角边”的运用
已知CD经过∠BCA的顶点C,CA=CB,E,F分别是CD上的两点.[问题1]如图1,若CD在∠BCA的内部,∠BCA=90°,AF⊥CD于点F,BE⊥CD于点E.求证:△CBE≌△ACF.[问题2]如图1,若CD在∠BCA的内部,∠BEC=∠CFA=∠α,0°<∠BCA < 180°,当∠α与∠BCA满足的条件为　　　　,可以使EF=BE-AF. [问题3]如图2,若CD在∠BCA的外部,∠BEC=∠CFA=∠BCA,请猜想EF,BE,AF三条线段之间的数量关系,并给出证明.[问题4]如图3,点D在边AB上,CA> AB,BD=2AD,∠BCA=∠1=∠2.若△CAB的面积为15,求△CBE与△ADF的面积之和.
[问题1]证明:∵AF⊥CD,BE⊥CD,∴∠BEC=∠CFA= 90°,∴∠CBE+∠BCE =90°.∵∠BCA=90°,∴∠BCE+∠ACF=90°,∴∠CBE=∠ACF.在△CBE和△ACF中,∵∠CBE=∠ACF,∠BEC=∠CFA,CB =AC,∴△CBE≌△ACF().[问题2]解:∠α+∠BCA=180°∵∠CBE+∠BCE=180°-∠BEC=180°-∠α,∠BCA=180°-∠α,∴∠CBE+∠BCE=∠BCA.∵∠ACF+∠BCE=∠BCA,∴∠CBE=∠ACF.在△BCE和△CAF中,∠CBE=∠ACF,BC=CA,∠BEC=∠CFA,∴△BCE≌△CAF(),∴BE =CF,CE =AF.∵EF= CF-CE,∴EF= BE-AF.
[问题3]解:EF=BE+AF.∵∠BEC=∠CFA=∠BCA,∠BCA+∠BCE+∠ACF=180°,∠CFA+∠CAF+∠ACF=180°,∴∠BCE=∠CAF.又∵BC=CA,∠BEC=∠CFA,∴△BCE≌△CAF(),∴BE=CF,EC=FA,∴EF=EC+CF=BE+AF.