


初中数学华师大版八年级上册2 线段垂直平分线作业课件ppt
展开知识点1 线段垂直平分线的性质定理
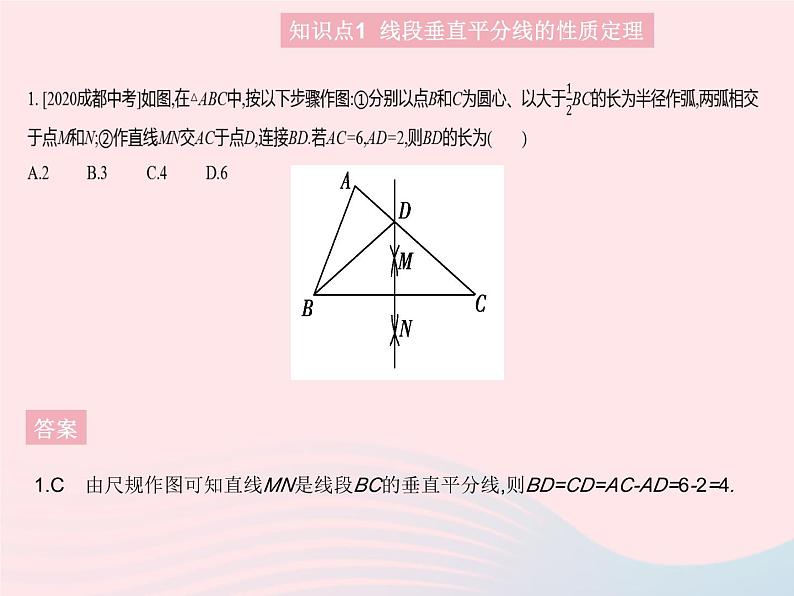
1.C 由尺规作图可知直线MN是线段BC的垂直平分线,则BD=CD=AC-AD=6-2=4.
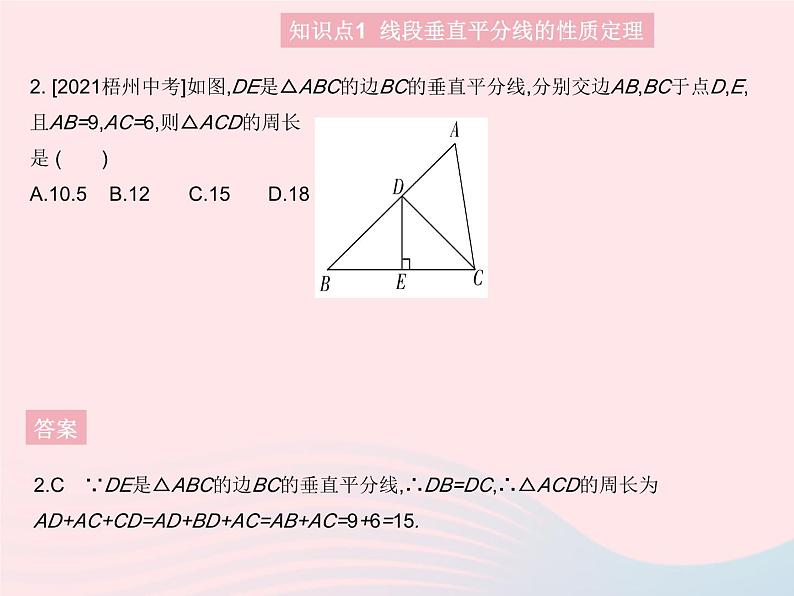
2. [2021梧州中考]如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是 ( )A.10.5B.12C.15D.18
2.C ∵DE是△ABC的边BC的垂直平分线,∴DB=DC,∴△ACD的周长为AD+AC+CD=AD+BD+AC=AB+AC=9+6=15.
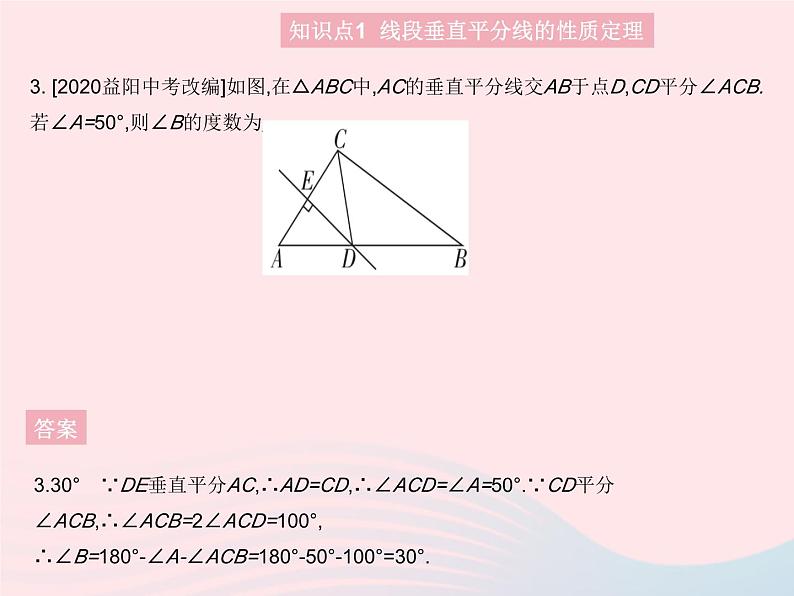
3. [2020益阳中考改编]如图,在△ABC中,AC的垂直平分线交AB于点D,CD平分∠ACB.若∠A=50°,则∠B的度数为 .
3.30° ∵DE垂直平分AC,∴AD=CD,∴∠ACD=∠A=50°.∵CD平分∠ACB,∴∠ACB=2∠ACD=100°,∴∠B=180°-∠A-∠ACB=180°-50°-100°=30°.
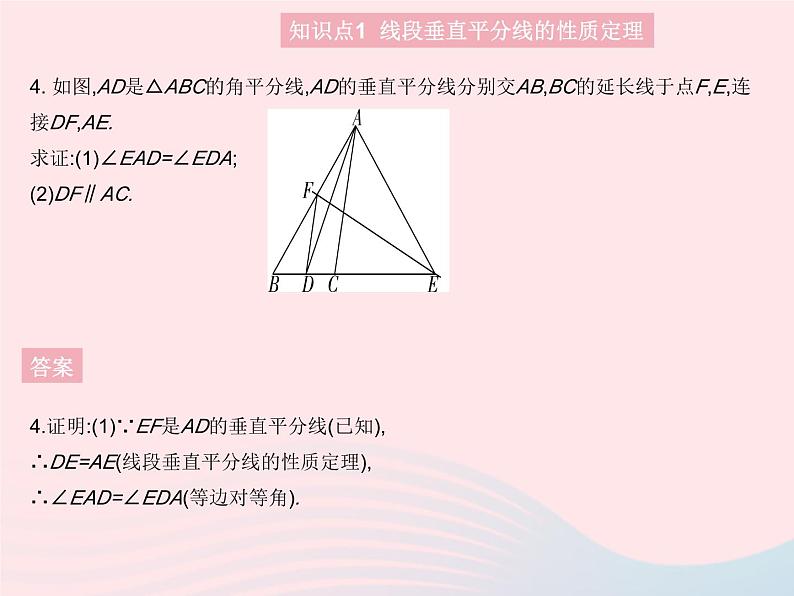
4. 如图,AD是△ABC的角平分线,AD的垂直平分线分别交AB,BC的延长线于点F,E,连接DF,AE.求证:(1)∠EAD=∠EDA;(2)DF∥AC.
4.证明:(1)∵EF是AD的垂直平分线(已知),∴DE=AE(线段垂直平分线的性质定理),∴∠EAD=∠EDA(等边对等角).
(2)∵EF为线段AD的垂直平分线(已知),∴FD=FA(线段垂直平分线的性质定理),∴∠FAD=∠FDA(等边对等角).∵AD平分∠BAC(已知),∴∠FAD=∠CAD(角平分线的定义),∴∠FDA=∠CAD(等量代换),∴DF∥AC(内错角相等,两直线平行).
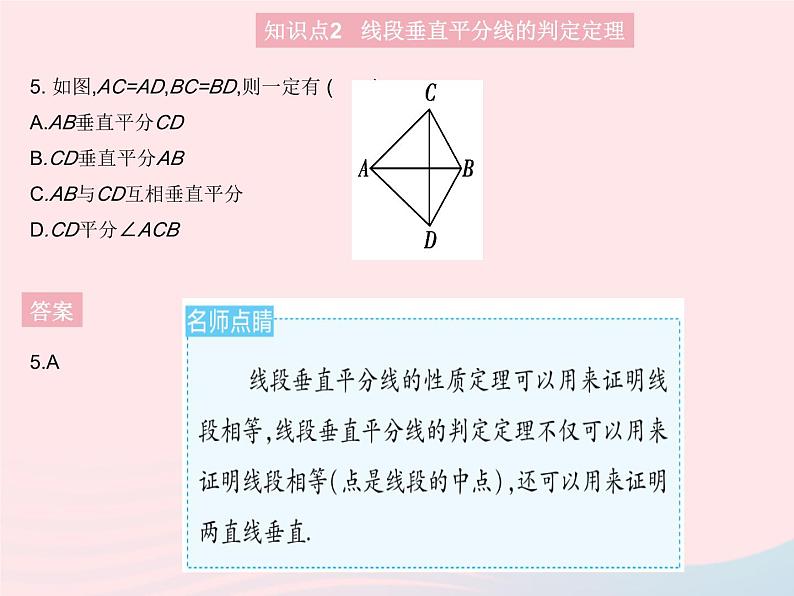
5. 如图,AC=AD,BC=BD,则一定有 ( )A.AB垂直平分CDB.CD垂直平分ABC.AB与CD互相垂直平分D.CD平分∠ACB
知识点2 线段垂直平分线的判定定理
6. [2022烟台期末]如图,若想建立一个货物中转仓,使其到A,B,C三地的距离相等,则中转仓的位置应选在 ( )A.三边垂直平分线的交点B.三边中线的交点C.三条角平分线的交点D.三边上高的交点
7. 如图,Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,连接CD,BE交于点F.求证:BE垂直平分CD.
7.证明:∵∠ACB=90°,DE⊥AB,∴∠ACB=∠BDE=90°.在Rt△BDE和Rt△BCE中,∵BD=BC(已知),BE=BE(公共边), ∴Rt△BDE≌Rt△BCE(H.L.),∴ED=EC(全等三角形的对应边相等).∵ED=EC(已证),BD=BC(已知),∴BE垂直平分CD(线段垂直平分线的判定定理).
1. [2021延边州期末]如图,直线l是线段AB的垂直平分线,点C在l外,且与点A在l的同一侧,点P是l上的任意一点,连接AP,BC,CP,则BC与AP+PC的大小关系是 ( )A.>B.
2. 如图,在△ABC中,AB=AC,用尺规作图的方法作出射线AD和直线EF,AD交EF于点O,连接BE,OC.下列结论不一定成立的是( )A.AE⊥BEB.EF平分∠AEBC.OA=OCD.AB=BE+EC
2.A 由题图可知,AD平分∠BAC,EF垂直平分AB.连接OB,∵AB=AC,AD平分∠BAC,∴AD垂直平分BC,∴OB=OC=OA,BE=AE,∴EF平分∠AEB,∴AB=AC=AE+EC=BE+EC,故选项B,C,D结论成立;只有当∠BAC=45°时,AE⊥BE,故选项A不一定成立.
3. 一题多解[2020南京中考]如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=39°,则∠AOC= °.
3.78 解法一 如图1,连接BO,并延长BO到P.∵线段AB,BC的垂直平分线l1,l2相交于点O,∴AO=OB=OC,∠BDO=∠BEO=90°,∴∠DOE+∠ABC=180°.∵∠DOE+∠1=180°,∴∠ABC=∠1=39°.∵OA=OB=OC,∴∠A=∠ABO,∠OBC=∠C.∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×39°=78°.解法二 如图2,连接OB.∵线段AB,BC的垂直平分线l1,l2相交于点O,∴AO=OB=OC,∴∠AOD=∠BOD,∠BOE=∠COE.∵∠DOE+∠1=180°,∠1=39°,∴∠DOE=141°,即∠BOD+∠BOE=141°,∴∠AOD+∠COE=141°,∴∠AOC=360°-(∠BOD+∠BOE)-(∠AOD+∠COE)=78°.
4. [2022湛江期末]如图,在△ABC中,AB=AC,BC=4,△ABC的面积是16,AC边的垂直平分线EF分别交AC,AB边于点E,F.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为 .
4.10 连接AM.因为EF垂直平分AC,所以MC=AM,要使△CDM的周长最小,则需AM+MD最小.易知A,M,D三点共线时AM+MD最小,此时因为AB=AC,点D为BC边的中点,所以∠ADC=90°.因为△ABC的面积是16,BC=4,所以AD=8,所以△CDM周长的最小值是AD+DC=8+2=10.
5. 如图,AB=CD,线段AC的垂直平分线与线段BD的垂直平分线相交于点E.求证:∠ABE=∠CDE.
5.证明:如图,连接AE,CE.∵AC,BD的垂直平分线相交于点E,∴AE=CE,BE=DE.在△ABE和△CDE中,∵AB=CD,AE=CE,BE=DE,∴△ABE≌△CDE(),∴∠ABE=∠CDE.
素养提升6. [2022阜阳期中]在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC(BC的延长线)于点M.(1)如图1,若∠A=40°,求∠NMB的大小.(2)如图2,如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的大小.(3)根据(1)(2)的计算,你能发现其中蕴含的规律吗?请写出你的猜想并证明.(4)如图3,将(1)中的∠A改为钝角,其余条件不变,对这个问题规律的认识是否需要加以修改?请你把∠A代入一个钝角度数验证你的结论.
初中数学华师大版八年级上册5 作已知线段的垂直平分线课文配套课件ppt: 这是一份初中数学华师大版八年级上册5 作已知线段的垂直平分线课文配套课件ppt,共18页。PPT课件主要包含了学习目标,生活中的数学,线段垂直平分线的判定,怎样证明这个结论呢,当堂练习,①②③等内容,欢迎下载使用。
初中数学华师大版八年级上册3 角平分线作业ppt课件: 这是一份初中数学华师大版八年级上册3 角平分线作业ppt课件,共22页。
华师大版八年级上册1 互逆命题与互逆定理作业ppt课件: 这是一份华师大版八年级上册1 互逆命题与互逆定理作业ppt课件,共10页。PPT课件主要包含了知识点1互逆命题等内容,欢迎下载使用。













