初中数学华师大版八年级上册3 角平分线作业ppt课件

这是一份初中数学华师大版八年级上册3 角平分线作业ppt课件，共22页。

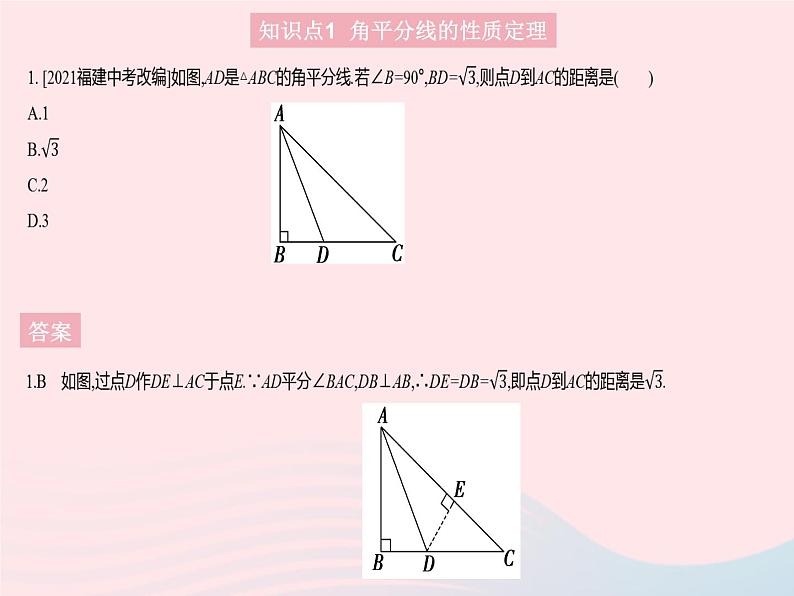
知识点1 角平分线的性质定理
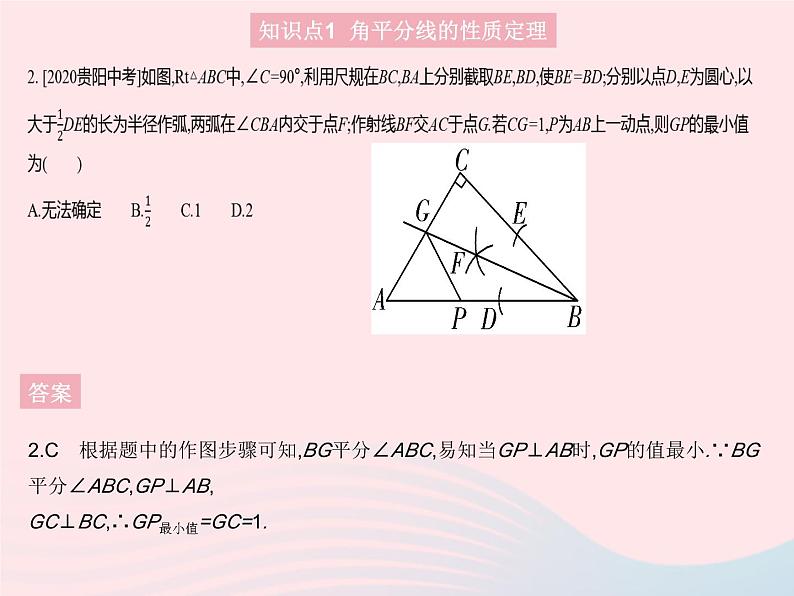
2.C　根据题中的作图步骤可知,BG平分∠ABC,易知当GP⊥AB时,GP的值最小.∵BG平分∠ABC,GP⊥AB,GC⊥BC,∴GP最小值=GC=1.
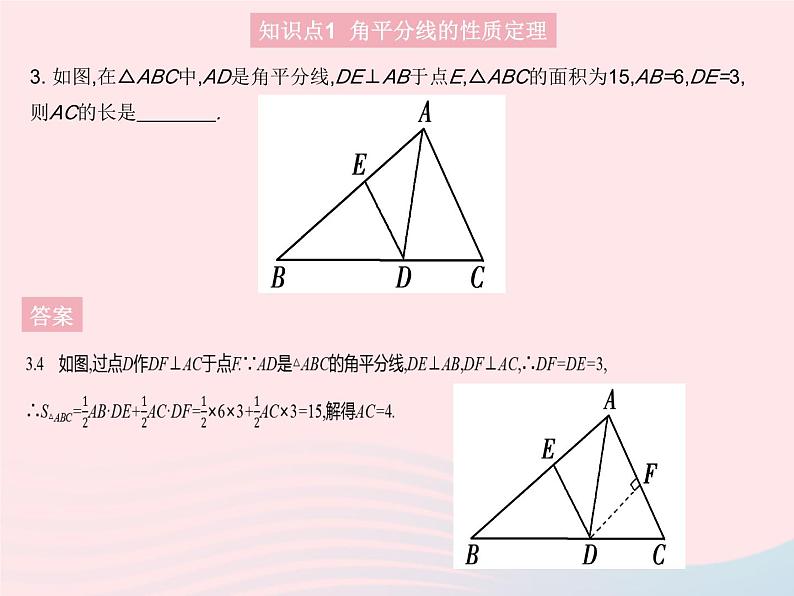
3. 如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为15,AB=6,DE=3,则AC的长是　　　　. 
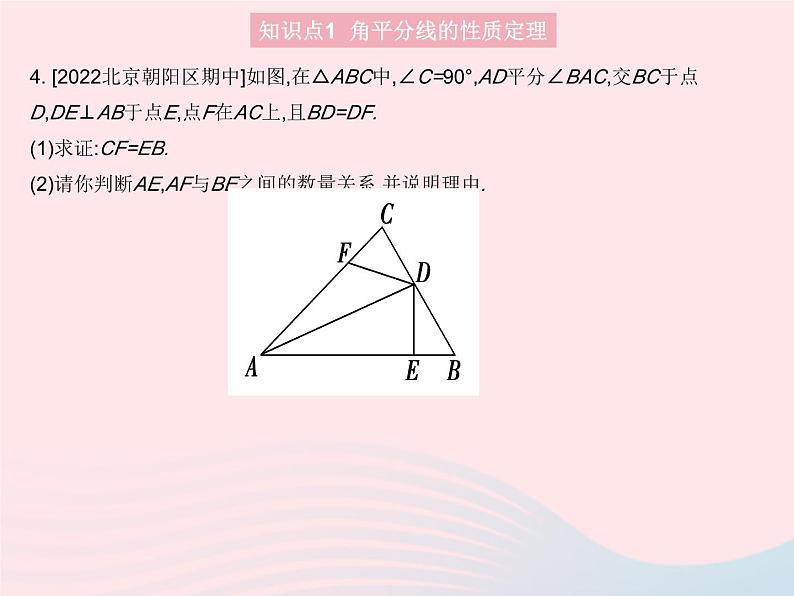
4. [2022北京朝阳区期中]如图,在△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,DE⊥AB于点E,点F在AC上,且BD=DF.(1)求证:CF=EB.(2)请你判断AE,AF与BE之间的数量关系,并说明理由.
4.(1)证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,∴DC=DE(角平分线的性质定理).在Rt△DCF和Rt△DEB中,∵DC=DE(已证),DF=DB(已知), ∴Rt△DCF≌Rt△DEB(H.L.),∴CF=EB(全等三角形的对应边相等).(2)解:AF+BE=AE.理由如下:在Rt△ADC和Rt△ADE中,∵DC=DE(已证),AD=AD(公共边),∴Rt△ADC≌Rt△ADE(H.L.),∴AC=AE(全等三角形的对应边相等).∵CF=EB,AC=AF+FC=AE,∴AF+BE=AE.
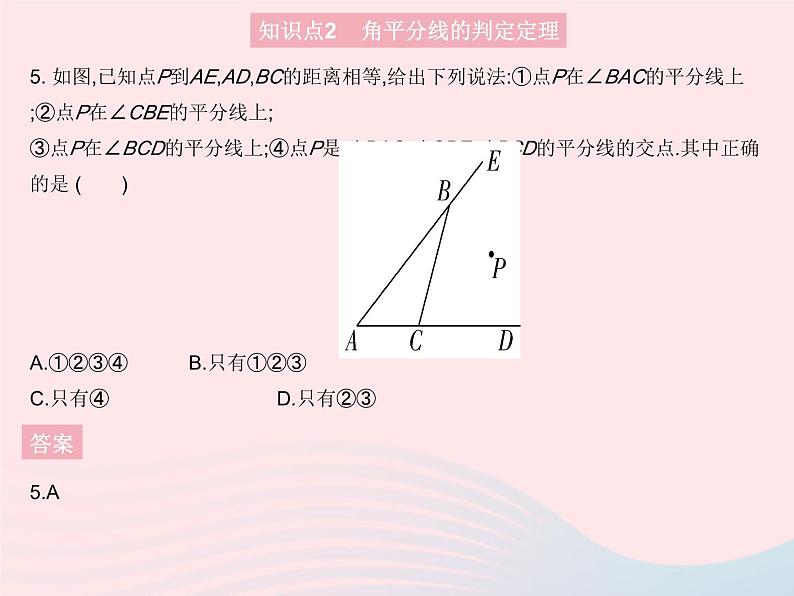
5. 如图,已知点P到AE,AD,BC的距离相等,给出下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P是∠BAC,∠CBE,∠BCD的平分线的交点.其中正确的是 (　　)A.①②③④B.只有①②③C.只有④ D.只有②③
知识点2 角平分线的判定定理
6. [2021济南期中]在9×7的网格中,∠AOB的位置如图所示,则到∠AOB两边距离相等的点是　　　　. 
6.M　到∠AOB两边距离相等的点在∠AOB的平分线上,结合题图,可知该点是M.
7. [2022大庆期末]如图,点D为锐角ABC内一点,点M在边BA上,点N在边BC上且DM=DN,∠BMD+∠BND=180°.求证:BD平分∠ABC.
7.证明:如图,过点D分别作DE⊥BA,DF⊥BC,垂足分别为点E,F.∵∠BMD+∠BND=180°(已知),∠BMD+∠EMD=180°,∴∠EMD=∠FND,又∵DM=DN(已知),∠DEM=∠DFN=90°,∴△DEM≌△DFN(),∴DE=DF(全等三角形的对应边相等),又∵DE⊥BA,DF⊥BC,∴BD平分∠ABC(角平分线的判定定理).
1. 教材P98练习T1变式 如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 (　　) A.一处B.两处C.三处D.四处
1.D　因为角的内部到角的两边的距离相等的点在角的平分线上,所以可供选择的地址可在这三条直线围成的三角形的内角平分线的交点处或这个三角形的外角平分线的交点处.如图,可供选择的地址有P1,P2,P3,P4,共四处.
2. [2022昆明期末]如图,△ABC的内角∠BAC与外角∠CBE的平分线相交于点P,E为AB的延长线上一点,BE=BC,PG∥AD交BC于点F,交AB于点G,连接CP,CE.给出下列结论:①∠ACB=2∠APB;②S△PAC∶S△PAB=PC∶PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有 (　　)A.①②④ B.①③④C.②③④ D.①②③
3. [2022东莞期末]如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB=　　　　°. 
4. 如图,△ABC的边BC的垂直平分线DP与∠BAC的平分线AD相交于点D,垂足为点P,连接BD,DC.若∠BAC=85°,则∠BDC=　　　　°. 
4.95　 如图,过点D作DE⊥AB,交AB的延长线于点E,过点D作DF⊥AC于点F.∵AD平分∠BAC,∴DE=DF.∵DP垂直平分BC,∴BD=CD.在Rt△DEB和Rt△DFC中,∵DB=DC,DE=DF,∴Rt△DEB≌Rt△DFC(H.L.),∴∠BDE=∠CDF,∴∠BDC=∠EDF.∵∠DEB=∠DFC=90°,∴∠EAF+∠EDF=360°-∠DEA-∠DFA=180°.∵∠BAC=85°,∴∠BDC=∠EDF=180°-85°=95°.
5. [2021苏州期中]如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,交BA的延长线于点F,且∠AEF=50°,连接DE.(1)求∠CAD的度数.(2)求证:DE平分∠ADC.
5.(1)解:∵EF⊥AB,∠AEF=50°,∴∠FAE=90°-50°=40°.∵∠BAD=100°,∴∠CAD=180°-100°-40°=40°.
(2)证明:如图,过点E作EG⊥AD于点G,EH⊥BC于点H.∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,∴EF=EG.∵BE平分∠ABC,EF⊥BF,EH⊥BC,∴EF=EH,∴EG=EH.∵EG⊥AD,EH⊥BC,∴DE平分∠ADC.
素养提升6. [2022济南段考]在△ABC中,∠ACB=2∠B.　　　 (1)如图1,当∠C=90°,AD为∠BAC的平分线时,求证:AB=AC+CD.(2)如图2,当∠C≠90°,AD为∠BAC的平分线时,线段AB,AC,CD之间又有怎样的数量关系?不需要证明,请直接写出你的猜想.(3)如图3,当AD平分△ABC的外角∠FAC时,线段AB,AC,CD之间有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
6.(1)证明:如图1,过点D作DE⊥AB于点E.∵AD为∠BAC的平分线,DC⊥AC,DE⊥AB,∴DE=DC,∠ACD=∠AED=90°.在Rt△ACD和Rt△AED中,∵AD=AD,DC=DE,∴Rt△ACD≌Rt△AED(H.L.),∴AC=AE.∵∠ACB=2∠B,∠AED=∠ACB,∠AED=∠B+∠EDB,∴∠B=∠EDB,∴BE=DE=DC,∴AB=BE+AE=CD+AC.(2)解:AB=CD+AC.