初中数学华师大版八年级上册1 全等三角形作业ppt课件

这是一份初中数学华师大版八年级上册1 全等三角形作业ppt课件，共10页。

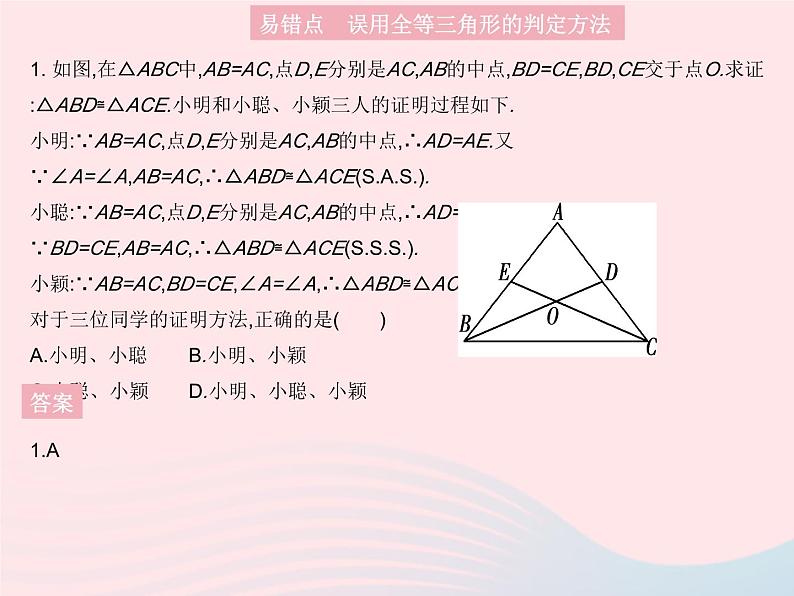
1. 如图,在△ABC中,AB=AC,点D,E分别是AC,AB的中点,BD=CE,BD,CE交于点O.求证:△ABD≌△ACE.小明和小聪、小颖三人的证明过程如下.小明:∵AB=AC,点D,E分别是AC,AB的中点,∴AD=AE.又∵∠A=∠A,AB=AC,∴△ABD≌△ACE().小聪:∵AB=AC,点D,E分别是AC,AB的中点,∴AD=AE.又∵BD=CE,AB=AC,∴△ABD≌△ACE().小颖:∵AB=AC,BD=CE,∠A=∠A,∴△ABD≌△ACE().对于三位同学的证明方法,正确的是(　　)A.小明、小聪B.小明、小颖C.小聪、小颖D.小明、小聪、小颖
易错点　误用全等三角形的判定方法
变式如图,已知点B,C,F,E在同一条直线上,FB=CE,AC=DF,∠B=∠E.求证:AB=ED.下面是李小虎同学证明的过程:∵FB=CE,∴FB-FC=CE-FC,即BC=EF.又∵AC=DF,∠B=∠E,∴△ABC≌△DEF(),∴AB=ED.上面的证明过程是否有错误?若有,请指出来,并给出正确的证明过程.
变式 解:题中的证明过程有错误,没有“”这个判定两个三角形全等的方法.正确的证明过程如下:如图,过点C,F分别作CM⊥AB于点M,FN⊥DE于点N.∵FB=CE,∴BC=EF.∵CM⊥AB,FN⊥DE,∴∠CMB=∠CMA=∠FND=∠FNE=90°.在△BCM和△EFN中,∵∠B=∠E,∠CMB=∠FNE,BC=EF,∴△BCM≌△EFN(),∴CM=FN,BM=EN.在Rt△ACM和Rt△DFN中,∵AC=DF,CM=FN,∴Rt△ACM≌Rt△DFN(H.L.),∴AM=DN.∴AM+BM=DN+EN,∴AB=DE.
疑难点　与全等三角形有关的探究型问题
1.解:在题图2中,结论仍成立,证明如下:过点D作DM⊥AC,DN⊥BC,垂足分别为M,N,则∠DME=∠DNF=∠MDN=90°.∵D为AB边的中点,∴AD=BD,在△ADM和△BDN中,∵∠A=∠B,∠AMD=∠BND=90°,AD=BD,∴△ADM≌△BDN(),∴DM=DN.∵∠MDN=∠EDF=90°,∴∠MDN-∠EDN=∠EDF-∠EDN,∴∠MDE=∠NDF.在△DME和△DNF中,∵∠DME=∠DNF,DM=DN,∠MDE=∠NDF,∴△DME≌△DNF(),∴S△DME=S△DNF,∴S四边形DMCN=S四边形DECF=S△DEF+S△CEF.