2023八年级数学上册第14章勾股定理专项2勾股定理与最短路径问题作业课件新版华东师大版

这是一份2023八年级数学上册第14章勾股定理专项2勾股定理与最短路径问题作业课件新版华东师大版，共11页。

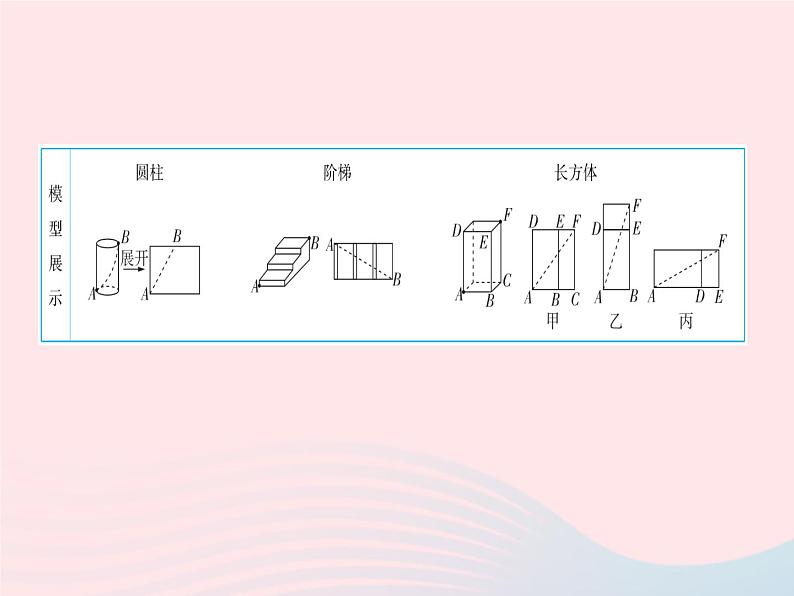
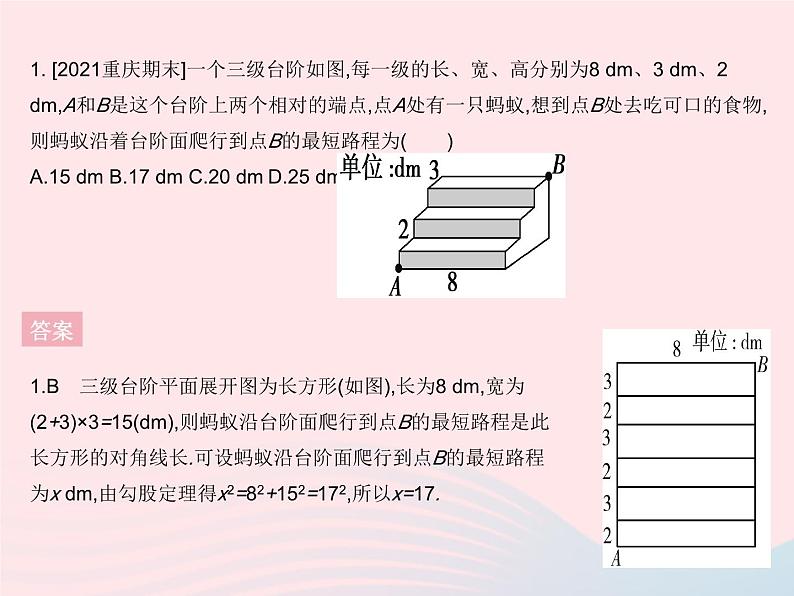
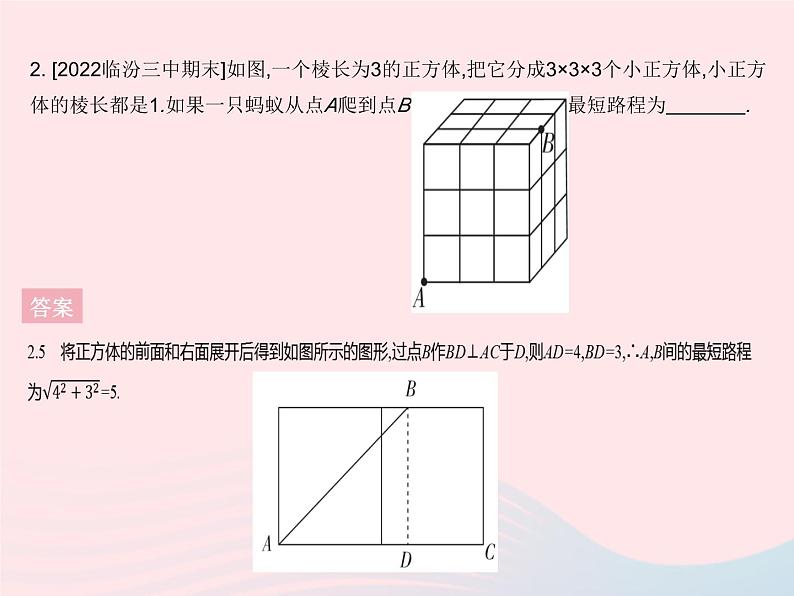
专项2　勾股定理与最短路径问题1. [2021重庆期末]一个三级台阶如图,每一级的长、宽、高分别为8 dm、3 dm、2 dm,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为(　　)A.15 dm B.17 dm C.20 dm D.25 dm答案1.B　三级台阶平面展开图为长方形(如图),长为8 dm,宽为(2+3)×3=15(dm),则蚂蚁沿台阶面爬行到点B的最短路程是此长方形的对角线长.可设蚂蚁沿台阶面爬行到点B的最短路程为x dm,由勾股定理得x2=82+152=172,所以x=17.2. [2022临汾三中期末]如图,一个棱长为3的正方体,把它分成3×3×3个小正方体,小正方体的棱长都是1.如果一只蚂蚁从点A爬到点B,那么估计A,B间的最短路程为　　　　. 答案 3. 如图,这是一个供滑板爱好者使用的U型池.该U型池可以看作是一个长方体去掉了一个“半圆柱”,中间可供滑行部分的截面是半径为8 m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=2 m.一滑板爱好者从A点滑到E点,则他滑行的最短距离约是多少?(边缘部分的厚度忽略不计,π取3)答案3.解:把“半圆柱”侧面展开后,连接AE,如图.由题意可知AD=8π≈8×3=24(m),DE=CD-CE=20-2=18(m).在Rt△ADE中,AE2=DE2+AD2≈182+242=900,所以AE≈30 m.所以他滑行的最短距离约是30 m.4. [2021武汉汉阳区期中]如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为　　　　cm.(杯壁厚度不计) 答案4.20　如图,将杯子侧面的一半展开,作点A关于EF的对称点A',连接A'B,则A'B即最短距离.在Rt△A'DB中,由勾股定理,得A'B2=A'D2+BD2=162+122=202,所以A'B=20 cm.5. H.E.杜登尼是19世纪英国知名的谜题创作者.“蜘蛛和苍蝇”问题最早出现在1903年的英国报纸上,它是杜登尼最有名的谜题之一.如图,在一个30英尺×12英尺×12英尺的长方体房间,一只蜘蛛在一面墙的中间离天花板1英尺的地方,苍蝇则在对面墙的中间离地板1英尺的地方.苍蝇是如此害怕,以至于无法动弹.试问,蜘蛛为了捉住苍蝇需要爬的最短路径长是多少?5.解:当按图1方式展开时,由题意可知在Rt△ABC中,∠C=90°,BC=32 英尺,AC=24 英尺,由勾股定理,得AB2=AC2+BC2=242+322=402,从而AB=40英尺.当按图2方式展开时,易知AB=42英尺.答案