2023八年级数学上册第14章勾股定理全章综合检测作业课件新版华东师大版

这是一份2023八年级数学上册第14章勾股定理全章综合检测作业课件新版华东师大版，共24页。

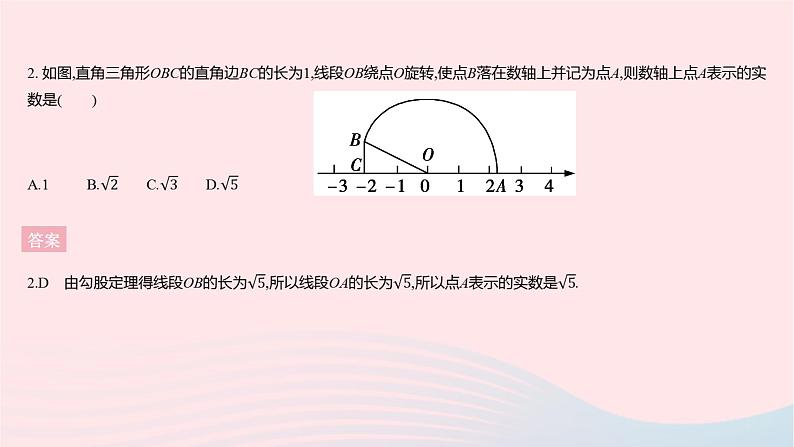
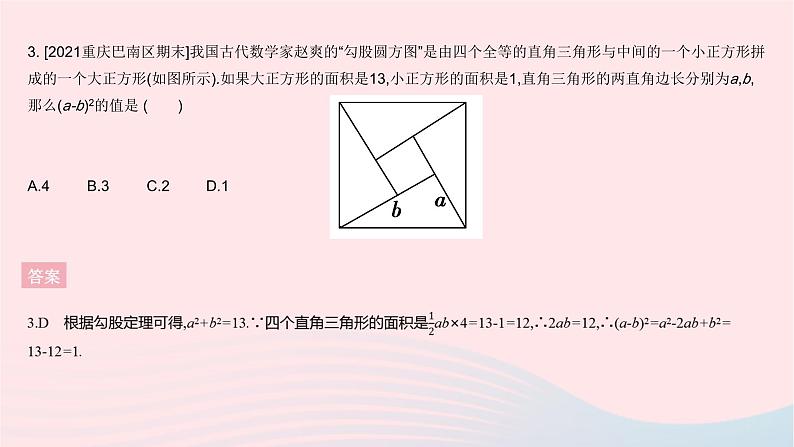
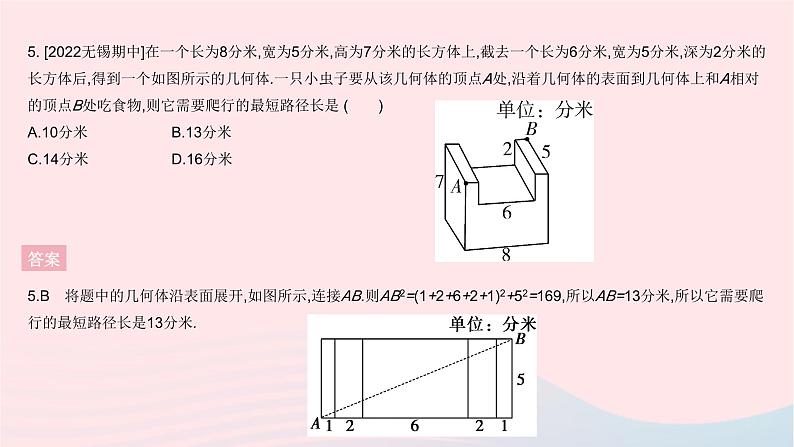
全章综合检测一、选择题1. 下列长度的三条线段能组成直角三角形的是(　　)A.3,4,5 B.2,3,4C.4,6,7 D.5,11,12答案1.A 答案 3. [2021重庆巴南区期末]我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a,b,那么(a-b)2的值是 (　　)A.4 B.3 C.2 D.1答案 4. 数学文化在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”译文:如图,有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,则绳索长(　　)A.12.5尺 B.13.5尺 C.14.5尺 D.15.5尺答案4.C　设绳索长x尺,根据勾股定理得,102+(x-4)2=x2,解得x=14.5,所以绳索长14.5尺.5. [2022无锡期中]在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只小虫子要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,则它需要爬行的最短路径长是 (　　)A.10分米 B.13分米C.14分米 D.16分米答案5.B　将题中的几何体沿表面展开,如图所示,连接AB.则AB2=(1+2+6+2+1)2+52=169,所以AB=13分米,所以它需要爬行的最短路径长是13分米. 答案  答案 8. 如图,在用6个边长均为1的小正方形构成的网格图中,∠α,∠β的顶点均在格点上,则∠α+∠β= (　　)A.75° B.60° C.45° D.30°答案8.C　如图,连接BE,CE,由勾股定理,得EB2=12+22=5,EC2=12+22=5,BC2=12+32=10,∴EB2+EC2=BC2,EB=EC,∴△EBC是等腰直角三角形,且∠EBC=45°.易证△ANC≌△BME,∴∠α=∠EBM,∴∠α+∠β=∠EBM+∠β=45°.二、填空题9. 用反证法证明“多边形中至多有三个锐角”时,假设多边形内角中存在四个锐角,则这四个锐角的外角和大于360°,这与　　　　　矛盾,所以多边形中至多有三个锐角. 答案9.多边形的外角和为360°  答案 11. [2021阜新中考]如图,折叠长方形纸片ABCD,使点B的对应点E落在CD边上,GH为折痕.已知AB=6,BC=10.当折痕GH最长时,线段BH的长为　　　　. 答案11.6.8　由题知,当E点与D点重合时GH最长,设BH=x,则CH=10-x,HE=BH=x.由勾股定理得,HC2+CE2=HE2,即(10-x)2+62=x2,解得x=6.8.12. [2021陕西中考改编]如图,AB,BC,CD,DE是四根长度均为5 cm的火柴棒,点A,C,E共线.若AC=6 cm,CD⊥BC,则线段CE的长度是　　　　 cm.  答案三、解答题13. 在正方形网格中,小正方形的顶点叫做格点,小华按下列要求作图:①在正方形网格的三条不同实线上各取一个格点,使其中任意两点不在同一条实线上;②连接三个格点,使之构成一个直角三角形.小华在左边的正方形网格中作出了Rt△ABC,请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并证明你所画出的图形是直角三角形.(要求:三个网格中的直角三角形互不全等)13.解:如图1, ∵MN2=22+42=20,NH2=12+32=10,MH2=12+32=10,∴MH2+NH2=MN2,∴△MNH是直角三角形.如图2,∵EF2=22+42=20,EG2=12+12=2,FG2=32+32=18,∴EG2+FG2=EF2,∴△EFG是直角三角形.答案14. [2022平顶山期中]为了积极响应国家新农村建设,某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧有一个村庄A,村庄A到公路MN的距离AB为600 m,假设宣讲车周围1 000 m以内(包括1 000 m处)能听到广播宣传,宣讲车以200 m/min的速度在公路MN上沿MB方向行驶,村庄A能听到广播宣传吗?若能,则总共能听到多长时间的广播宣传?14.解:∵村庄A到公路MN的距离为600 m,600<1 000,∴村庄A能听到广播宣传.假设当宣讲车行驶到P点(P点在MB中间)时,村庄A开始听到广播宣传,行驶到Q点(Q点在BN中间)时,村庄A开始不能听到广播宣传,则AP=AQ=1 000 m,AB=600 m.在Rt△ABP中,由勾股定理得,BP2=AP2-AB2,∴BP=BQ=800(m),∴PQ=BP+BQ=1 600 m,∴村庄A能听到广播宣传的时间为1 600÷200=8(min).答案15. 拉杆箱是人们出行的常用品,采用拉杆箱可以让人们出行更轻松.如图,某种拉杆箱的箱体AB长65 cm,拉杆最大伸长距离BC为35 cm,在箱体底端装有一圆形滚轮,当拉杆拉到最长时,滚轮的圆心在图中的A处,点A到地面(用DN表示)的距离AD为3 cm,当拉杆全部缩进箱体时,滚轮圆心水平向右平移55 cm到A'处,求拉杆把手C离地面的距离.(假设C点的位置保持不变)15.解:如图,过点C作CE⊥DN于点E,延长AA'交CE于点F,则∠AFC=90°.设A'F=x cm,则AF=(55+x)cm.由题可得AC=65+35=100(cm),A'C=65 cm.在Rt△A'CF中,CF2=A'C2-A'F2=652-x2.在Rt△ACF中,CF2=1002-(55+x)2.∴652-x2=1002-(55+x)2,解得x=25,∴A'F=25 cm,∴CF2=652-252=3 600,∴CF=60 cm.∵EF=AD=3 cm,∴CE=CF+EF=60+3=63(cm),∴拉杆把手C离地面的距离为63 cm.答案16. [2022扬州树人学校期中]如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.(1)当t=　　　　时,△CBD是直角三角形; (2)若△CBD是等腰三角形,求t的值. 答案③BD=BC时,如图,过点B作BF⊥AC于点F.根据等腰三角形三线合一的性质可得CF=DF.∵BF=12,∴CF2=BC2-BF2=92,∴CF=9,∴CD=2CF=9×2=18,∴t=18÷2=9.综上所述,t=6.25或7.5或9时,△CBD是等腰三角形.