2023八年级数学上册第14章勾股定理章末培优专练作业课件新版华东师大版

这是一份2023八年级数学上册第14章勾股定理章末培优专练作业课件新版华东师大版，共18页。

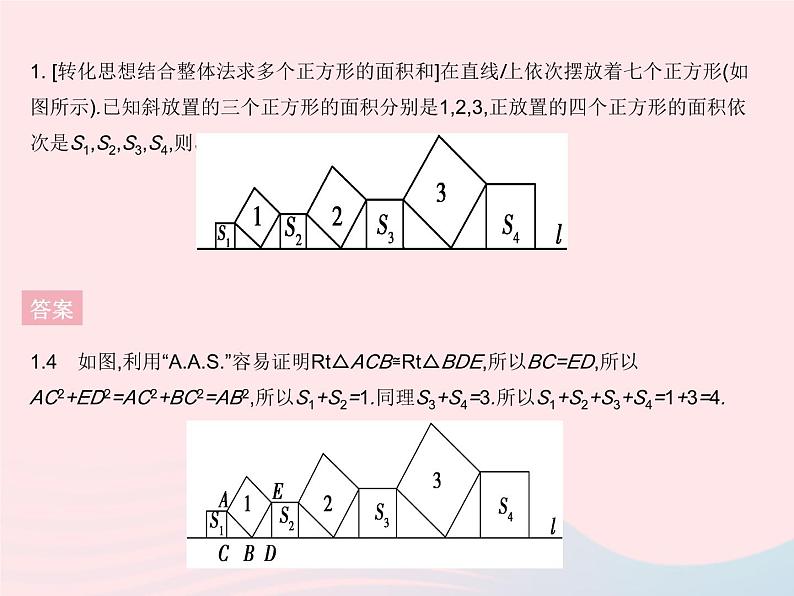
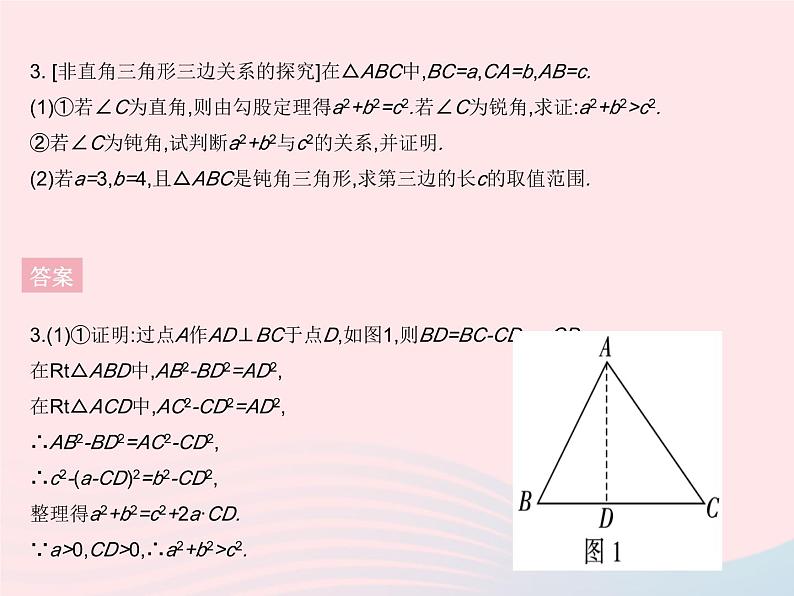
章末培优专练1. [转化思想结合整体法求多个正方形的面积和]在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=　　　　. 答案1.4　如图,利用“A.A.S.”容易证明Rt△ACB≌Rt△BDE,所以BC=ED,所以AC2+ED2=AC2+BC2=AB2,所以S1+S2=1.同理S3+S4=3.所以S1+S2+S3+S4=1+3=4.2. 已知Rt△ABC的两条直角边长分别为a和b,斜边长为c,斜边上的高为h,试判断以h,c+h,a+b为边长的三角形的形状,并说明理由.答案 3. [非直角三角形三边关系的探究]在△ABC中,BC=a,CA=b,AB=c.(1)①若∠C为直角,则由勾股定理得a2+b2=c2.若∠C为锐角,求证:a2+b2>c2.②若∠C为钝角,试判断a2+b2与c2的关系,并证明.(2)若a=3,b=4,且△ABC是钝角三角形,求第三边的长c的取值范围.答案3.(1)①证明:过点A作AD⊥BC于点D,如图1,则BD=BC-CD=a-CD.在Rt△ABD中,AB2-BD2=AD2,在Rt△ACD中,AC2-CD2=AD2,∴AB2-BD2=AC2-CD2,∴c2-(a-CD)2=b2-CD2,整理得a2+b2=c2+2a·CD.∵a>0,CD>0,∴a2+b2>c2. 4. [利用勾股定理进行方案设计]如图,A,B是公路l(l为东西走向)同旁的两个村庄,A村到公路l的距离AC=2 km,B村到公路l的距离BD=4 km,CD=8 km.(1)求出A,B两村之间的距离的平方的值;(2)为了方便运输两村的垃圾,现计划在公路边建一个垃圾中转站M,要求该垃圾中转站到两村的距离之和最小,并求距离之和的最小值;(3)为方便村民出行,计划在公路边新建一个公共汽车站P,要求该站到两村的距离相等,请用尺规在图中作出点P的位置.(保留清晰的作图痕迹,不写作法)答案4.解:(1)如图1,连接AB,过点A作AE⊥BD于点E,则AE=CD=8 km,BE=BD-AC=2 km.在Rt△ABE中,由勾股定理,得AB2=AE2+BE2=82+22=68,所以A,B两村之间的距离的平方的值为68.(2)如图2,作点A关于直线l的对称点A',连接A'B交直线l于点M,连接MA,MB,则点M即所求作的点,此时MA+MB的值最小.过点A'作A'F⊥BD,交BD的延长线于点F,则BF=BD+DF=BD+A'C=BD+AC=4+2=6(km),A'F=CD=8 km.在Rt△A'BF中,由勾股定理,得A'B2=82+62=100,从而A'B=10 km,所以距离之和的最小值为10.(3)如图3,连接AB,作AB的垂直平分线GH,交直线l于点P,连接PA,PB,则PA=PB,所以点P即所求.1 [2021滨州中考]在Rt△ABC中,若∠C=90°,AC=3,BC=4,则点C到直线AB的距离为 (　　)A.3 B.4 C.5 D.2.4答案  答案  答案 4. 新考法[2021常德中考]阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即m=a2+b2,那么称m为广义勾股数,给出下面四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.其中正确的是 (　　)A.②④ B.①②④ C.①② D.①④答案4.C　①∵7不能表示为两个正整数的平方和,∴7不是广义勾股数,故结论①正确;②∵13=22+32,∴13是广义勾股数,故结论②正确;③两个广义勾股数的和不一定是广义勾股数,如5和10是广义勾股数,但是它们的和不是广义勾股数,故结论③错误;④设m1=a2+b2,m2=c2+d2,则m1·m2=(a2+b2)·(c2+d2)=a2c2+a2d2+b2c2+b2d2=(a2c2+b2d2+2abcd)+(a2d2+b2c2-2abcd)=(ac+bd)2+(ad-bc)2,当a=c,b=d时,ad-bc=0,∴两个广义勾股数的积不一定是广义勾股数,故结论④错误,∴正确的是①②.5. [2020绥化中考]在Rt△ABC中,∠C=90°.若AB-AC=2,BC=8,则AB的长是　　　　　. 答案5.17　根据题意得,AC2+BC2=AB2,所以(AB-2)2+82=AB2,所以AB=17.6. 数学文化[2021宿迁中考]《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图),水深和芦苇长各多少尺?则该问题的水深是　　　尺. 答案6.12　如图,设芦苇长AC=AC'=x尺,则水深AB=(x-1)尺,∵C'E=10尺,∴C'B=5尺.在Rt△AC'B中,由勾股定理,得C'B2+AB2=AC'2,∴52+(x-1)2=x2,解得x=13,即芦苇长13尺,水深为12尺.7. [2020雅安中考]对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AD=2,BC=4,则AB2+CD2=　　　　　. 答案7.20　因为AC⊥BD,所以∠AOD=∠AOB=∠BOC=∠COD=90°.由勾股定理,得AB2+CD2=AO2+BO2+CO2+DO2,AD2+BC2=AO2+DO2+BO2+CO2,所以AB2+CD2=AD2+BC2.因为AD=2,BC=4,所以AB2+CD2=22+42=20.8. [2020苏州中考]如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC=　　　　　. 答案8.1　设AE=ED=x,CD=y,∴BD=2y.∵AD⊥BC,∴∠ADB=∠ADC=90°.在Rt△ABD中,AB2=AD2+BD2=4x2+4y2=4,∴x2+y2=1.在Rt△CDE中,EC2=x2+y2=1,∴EC=1.