2023七年级数学下册第9章多边形易错疑难集训作业课件新版华东师大版

这是一份2023七年级数学下册第9章多边形易错疑难集训作业课件新版华东师大版，共8页。

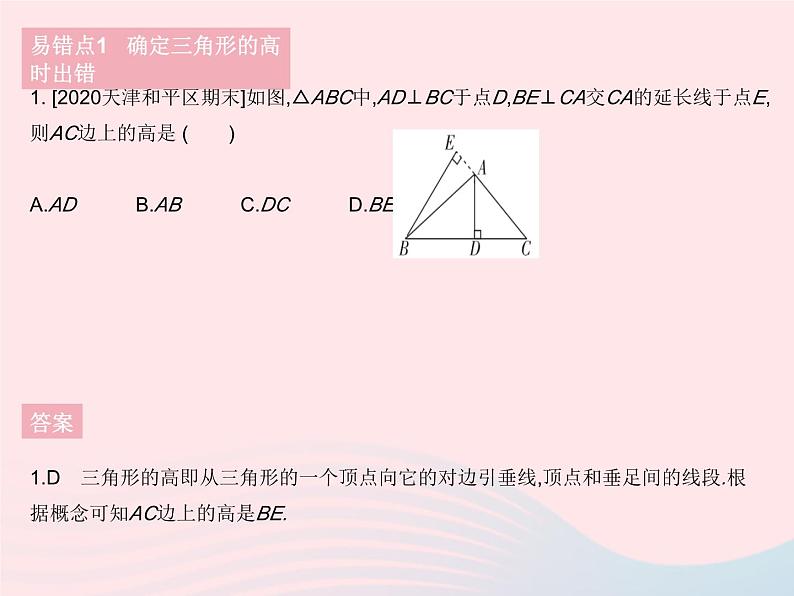
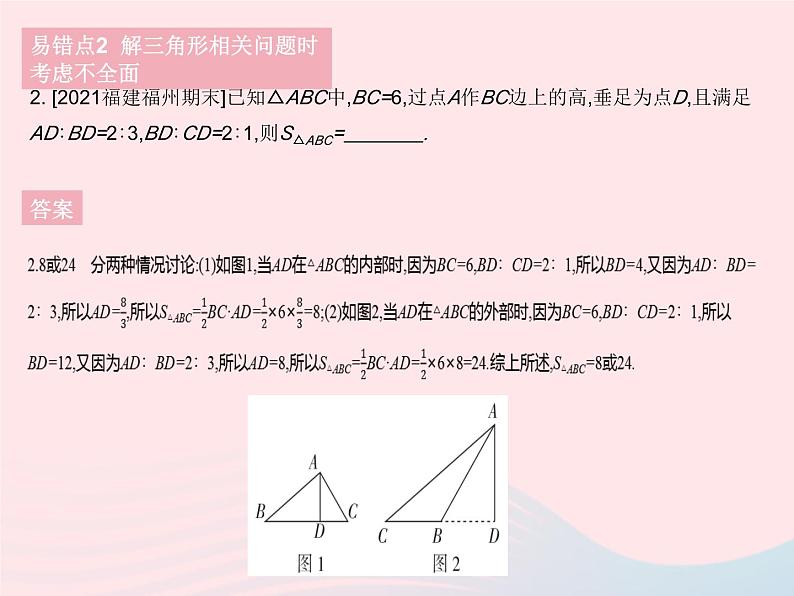
易错疑难集训1. [2020天津和平区期末]如图,△ABC中,AD⊥BC于点D,BE⊥CA交CA的延长线于点E,则AC边上的高是 (　　)　　　　　 　　　　　　　　　　A.AD　　　B.AB　　　C.DC　　　D.BE易错点1 确定三角形的高时出错答案1.D　三角形的高即从三角形的一个顶点向它的对边引垂线,顶点和垂足间的线段.根据概念可知AC边上的高是BE.2. [2021福建福州期末]已知△ABC中,BC=6,过点A作BC边上的高,垂足为点D,且满足AD∶BD=2∶3,BD∶CD=2∶1,则S△ABC=　　　　. 易错点2 解三角形相关问题时考虑不全面答案 [变式]在△ABC中,∠A=50°,高BE,CF所在直线交于点O,且点E,F不与点C,B重合,求∠BOC的度数.易错点2 解三角形相关问题时考虑不全面答案[变式]解:当交点O在三角形内部时,如图1,因为∠AFO=∠AEO=90°,∠A=50°,所以∠OCB=90°-∠ABC,∠OBC=90°-∠ACB,∠BOC=180°-(∠OCB+∠OBC)=180°-∠A=130°.当交点O在三角形外部时,如图2,在△AFC中,∠A=50°,∠AFC=90°,故∠1=90°-50°=40°.因为∠1=∠2,所以∠2=40°,又因为∠CEO=90°,所以∠EOC=90°-40°=50°,即∠BOC=50°.综上,∠BOC=130°或50°.1. 如图,把△ABC的三边BA,CB和AC分别向外延长一倍,将得到的点A',B',C'顺次连接成△A'B'C'.若△ABC的面积是5,求△A'B'C'的面积.疑难点 三角形的中线与高的应用答案1.解:如图,连接AB',BC',CA'.由题意,得AB=AA',BC=BB',AC=CC',所以S△AA'B'=S△ABB'=S△ABC=S△BCC'=S△AA'C=S△BB'C'=S△A'C'C=5,所以S△A'B'C'=5×7=35.2. 如图,在△ABC中,AB=AC,P是底边BC上的任意一点(不与点B,C重合),CD⊥AB于点D,PE⊥AB于点E,PF⊥AC于点F.请说明CD=PE+PF.答案 疑难点 三角形的中线与高的应用