





冀教版八年级上册17.1 等腰三角形作业课件ppt
展开1. [2021德州期中]下列条件中,不能判定△ABC是等腰三角形的是 ( )A.a=3,b=3,c=4B.a∶b∶c=2∶3∶4C.∠B=50°,∠C=80°D.∠A∶∠B∶∠C=1∶1∶2
知识点1 等腰三角形的判定定理: 等角对等边
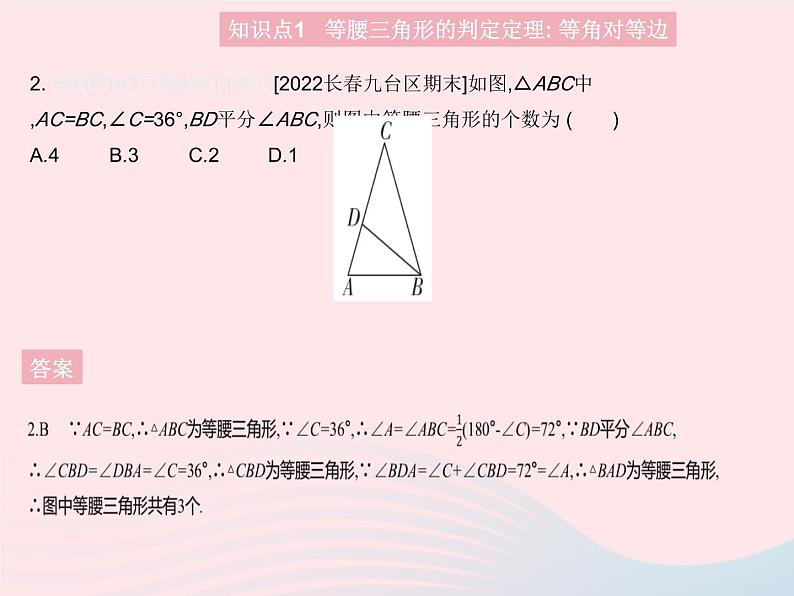
1.B A项,∵a=3,b=3,c=4,∴a=b,∴△ABC是等腰三角形;B项,∵a∶b∶c=2∶3∶4,∴a≠b≠c,∴△ABC不是等腰三角形;C项,∵∠B=50°,∠C=80°,∴∠A=180°-∠B-∠C=50°,∴∠A=∠B,∴AC=BC,∴△ABC是等腰三角形;D项,∵∠A∶∠B∶∠C=1∶1∶2,∴∠A=∠B,∴AC=BC,∴△ABC是等腰三角形.
2. 教材P143习题A组T1变式[2022长春九台区期末]如图,△ABC中,AC=BC,∠C=36°,BD平分∠ABC,则图中等腰三角形的个数为 ( )A.4B.3C.2D.1
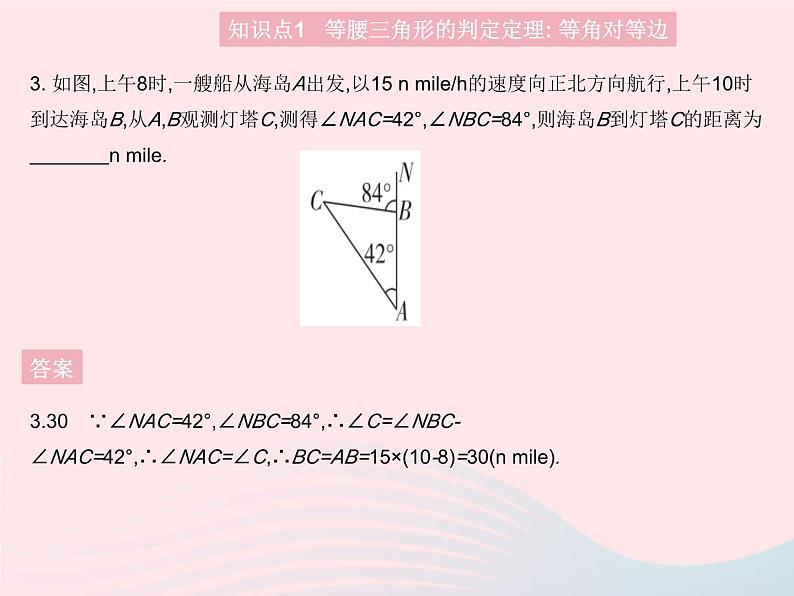
3. 如图,上午8时,一艘船从海岛A出发,以15 n mile/h的速度向正北方向航行,上午10时到达海岛B,从A,B观测灯塔C,测得∠NAC=42°,∠NBC=84°,则海岛B到灯塔C的距离为 n mile.
3.30 ∵∠NAC=42°,∠NBC=84°,∴∠C=∠NBC-∠NAC=42°,∴∠NAC=∠C,∴BC=AB=15×(10-8)=30(n mile).
4. [2022保定期中]如图,在△ABC中,AB=AC,M,N分别是AB,AC边上的点,并且MN∥BC.(1)求证:△AMN是等腰三角形.(2)若点P是MN上的一点,并且BP平分∠ABC,求证:△BPM是等腰三角形.
4.证明:(1)∵AB=AC,∴∠ABC=∠C,∵MN∥BC,∴∠AMN=∠ABC,∠ANM=∠C,∴∠AMN=∠ANM,∴AM=AN,∴△AMN是等腰三角形.
(2)∵BP平分∠ABC,∴∠MBP=∠CBP,∵MN∥BC,∴∠MPB=∠CBP,∴∠MBP=∠MPB,∴MB=MP,∴△BPM是等腰三角形.
5. [2021深圳罗湖区期末]下列条件中,不能判定△ABC是等边三角形的是 ( )A.∠A=∠B=∠CB.AB=AC,∠B=60°C.∠A=60°,∠B=60°D.AB=AC,且∠B=∠C
知识点2 等边三角形的判定定理
5.D A项,由“三个角都相等的三角形是等边三角形”可以判定△ABC是等边三角形;B项,由“有一个角是60°的等腰三角形是等边三角形”可以判定△ABC是等边三角形;C项,∵∠A=60°,∠B=60°,∴∠A=∠B=∠C=60°,∴△ABC是等边三角形;D项,只能判定△ABC是等腰三角形.
6. [2022北京日坛中学期中]如图,在一个池塘两旁有一条笔直的小路(B,C为小路端点)和一棵小树(A为小树位置),测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48米,则AC= 米.
6.48 由∠ACB=∠ABC=60°,易知△ABC为等边三角形,所以AC=BC=48米.
7. 如图,在△ABC中,AB=AC,∠A=60°,EF∥AB.判断△CEF的形状,并说明理由.
7.解:△CEF是等边三角形.理由如下:∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠B=∠C=60°,∵EF∥AB,∴∠CEF=∠A=60°,∠CFE=∠B=60°,∴∠C=∠CEF=∠CFE,∴△CEF是等边三角形.
8. 已知:如图,线段a,∠α.求作:△ABC,使∠A=∠α,AB=AC,且BC边上的高AD=a.(要求:用尺规作图,保留作图痕迹,不写作法和证明)
知识点3 尺规作图
8.解:如图,△ABC即所求作的三角形,其中∠CAB=∠α,AD=a,AB=AC.
1. 如图,∠BAC=100°,∠B=40°,∠D=20°,AB=3,则CD=( )A.2B.3C.4D.5
1. B 在△ABC中,∠BAC=100°,∠B=40°,所以∠ACB=40°,所以∠B=∠ACB,所以AB=AC.因为∠D=20°,所以∠CAD=∠ACB-∠D=20°,所以∠D=∠CAD,所以AC=CD,所以CD=AB=3.
2. [2022承德期末]如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若BD=1,BC=3,则AC的长为( )A.3B.4C.5D.6
2.C 如图,延长BD交AC于E,由CD平分∠ACB,BD⊥CD,易知△BCD≌△ECD,∴CE=BC=3,∴△BCE为等腰三角形,∴DE=BD=1,∵∠A=∠ABD,∴AE=BE=2,∴AC=AE+CE=2+3=5.
3. 原创题在Rt△ABC中,∠C=90°,∠A=30°,点D在边AB上,连接CD.给出下列四种说法:①当DC=DB时,△BCD一定为等边三角形;②当AD=CD时,△BCD一定为等边三角形;③当△ACD 是等腰三角形时,△BCD一定为等边三角形;④当△BCD 是等腰三角形时,△ACD一定为等腰三角形.其中正确的说法是 .(填序号)
3.①②④ ∵∠C=90°, ∠A=30°,∴∠B=60°.①当DC=DB时,由“有一个角是60°的等腰三角形是等边三角形”可判定△BCD为等边三角形;②当AD=CD时,∠ACD=∠A=30°,∴∠BCD=∠BDC=60°,易知△BCD为等边三角形;③当△ACD 是等腰三角形,且顶角∠A=30°时,△BCD不是等边三角形;④当△BCD 是等腰三角形时,∵∠B=60°,∴△BCD为等边三角形,∴∠BDC=60°,∴∠ACD=30°,∴∠ACD=∠A,∴AD=CD,∴△ACD为等腰三角形.综上,正确的说法是①②④.
4. 如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G,F.若FG=2,ED=4,则BE+CD的值为 .
4.6 ∵ED∥BC,∴∠EGB=∠GBC,∠DFC=∠FCB.∵BG和CF分别平分∠ABC和∠ACB,∴∠GBC=∠GBE,∠FCB=∠FCD,∴∠EGB=∠EBG,∠DCF=∠DFC,∴BE=EG,CD=DF.∵FG=2,ED=4,∴BE+CD=EG+DF=EF+FG+FG+DG=ED+FG=6.
5. [2021杭州期中]如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)(2)请选择(1)中的一种情形,写出证明过程.
5.解:(1)①②;①③.
6. [2022石家庄期末]在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.(1)当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE DB(填“>”“<”或“=”). (2)当E不是AB的中点时,AE与DB的大小关系是:AE DB(填“>”“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F.请你继续按照这种思路完成全部解答过程. (3)在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为2,AE=4,则CD的长为 .(直接写出答案)
6.解:(1)=∵△ABC是等边三角形,∴∠ABC=60°,AC=BC,∵点E为AB的中点,∴CE平分∠ABC,AE=BE,∴∠BCE=30°,∵ED=EC,∴∠EDB=∠BCE=30°,∴∠DEB=∠ABC-∠EDB=30°,∴∠DEB=∠EDB,∴BD=BE,∴AE=DB.
初中冀教版17.1 等腰三角形作业课件ppt: 这是一份初中冀教版17.1 等腰三角形作业课件ppt,共12页。PPT课件主要包含了类型1求角度,类型2求线段的长度等内容,欢迎下载使用。
初中冀教版17.5 反证法作业ppt课件: 这是一份初中冀教版17.5 反证法作业ppt课件,共10页。PPT课件主要包含了∠B≥90°等内容,欢迎下载使用。
初中17.3 勾股定理作业课件ppt: 这是一份初中17.3 勾股定理作业课件ppt,共20页。













