2023七年级数学下册第七章相交线与平行线学科素养拓训上课课件新版冀教版

这是一份2023七年级数学下册第七章相交线与平行线学科素养拓训上课课件新版冀教版，共6页。

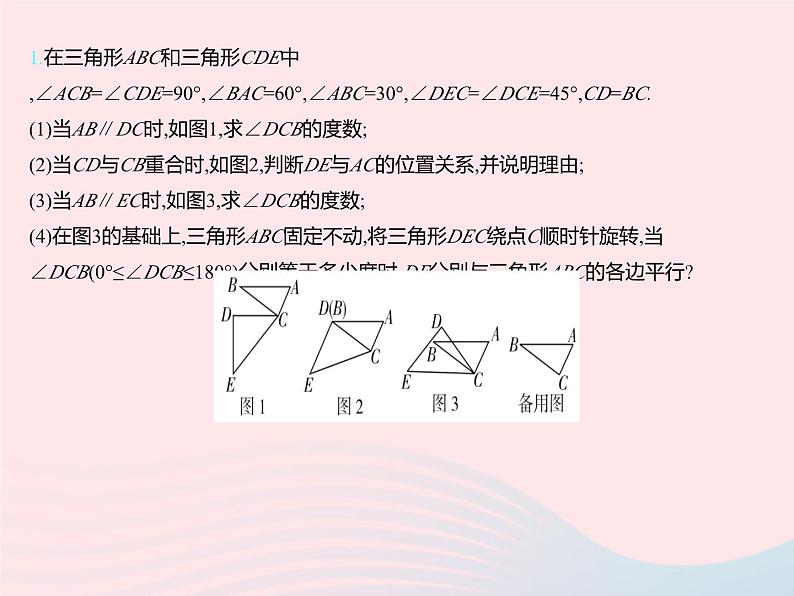
学科素养拓训1.在三角形ABC和三角形CDE中,∠ACB=∠CDE=90°,∠BAC=60°,∠ABC=30°,∠DEC=∠DCE=45°,CD=BC.(1)当AB∥DC时,如图1,求∠DCB的度数;(2)当CD与CB重合时,如图2,判断DE与AC的位置关系,并说明理由;(3)当AB∥EC时,如图3,求∠DCB的度数;(4)在图3的基础上,三角形ABC固定不动,将三角形DEC绕点C顺时针旋转,当∠DCB(0°≤∠DCB≤180°)分别等于多少度时,DE分别与三角形ABC的各边平行?答案1.解:(1)因为AB∥DC,∠ABC=30°,所以∠DCB=∠ABC=30°.(2)DE∥AC.理由如下:因为∠ACB=∠CDE=90°,所以DE∥AC.(3)因为AB∥EC,所以∠BCE=∠ABC=30°,又因为∠DCE=45°,所以∠DCB=∠DCE-∠BCE=15°.(4)当∠DCB=60°或120°时,DE∥AB,如图甲. 当∠DCB=90°时,DE∥CB,如图乙.当∠DCB=0°或180°时,DE∥AC,如图丙.2.[与物理知识结合的平行线问题]材料1:反射定律当入射光线AO照射到平面镜上时,将遵循平面镜反射定律,即反射角(∠BOM)的大小等于入射角(∠AOM)的大小,显然,这两个角的余角也相等,其中法线(OM)与平面镜垂直,并且满足入射光线、反射光线(OB)与法线在同一个平面.材料2:平行逃逸角对于某定角∠AOB=α(0°<α<90°),点P为边OB上一点,从点P发出一光线PQ(射线),∠BPQ=β(0°<β<90°),当光线PQ接触到边OA和OB时会遵循反射定律发生反射,当光线PQ经过n次反射后与边OA或OB平行时,称角β为定角α的n阶平行逃逸角,特别地,当光线PQ直接与OA平行时,称角β为定角α的0阶平行逃逸角.(1)已知∠AOB=α=20°,①如图1,若PQ∥OA,则∠BPQ=　　　 °,即该角为角α的0阶平行逃逸角; ②如图2,经过一次反射后的光线P1Q∥OB,此时的∠BPP1为α的1阶平行逃逸角,求∠BPP1的大小;③若经过两次反射后的光线与OA平行,请补全图3,并直接写出角α的2阶平行逃逸角为　　　　°. (2)根据(1)的结论,归纳猜想对于任意角α(0°<α<90°),其n(n为自然数)阶平行逃逸角β=　　　　 (用含n和α的代数式表示). 答案2.解:(1)①20因为PQ∥OA,所以∠BPQ=∠AOB=20°.②在题图2中,由反射定律得,∠AP1Q=∠PP1O,因为P1Q∥OB,所以∠AP1Q=∠AOB=20°,∠BPP1+∠QP1P=180°,又因为∠AP1Q+∠PP1O+∠QP1P=180°,所以∠BPP1=∠AP1Q+∠PP1O=2∠AOB=40°.③60补全图形如图所示. (2)(n+1)α由(1)可知,角α的0阶平行逃逸角为α,角α的1阶平行逃逸角为2α,角α的2阶平行逃逸角为3α,‧‧‧,由此可以推出,角α的n阶平行逃逸角为(n+1)α.