初中数学8.4 整式的乘法课堂教学课件ppt

这是一份初中数学8.4 整式的乘法课堂教学课件ppt，共21页。PPT课件主要包含了归纳总结，名师点睛等内容，欢迎下载使用。

1.[2020广东深圳盐田区外国语学校段考]计算(a-2)(a+3)的结果是(　　)　　　　　 　　　　　　　　　　A.a2-6B.a2+a-6C.a2+6D.a2-a+6
1.B　(a-2)(a+3)=a2+3a-2a-6=a2+a-6.
多项式与多项式相乘的注意事项　　(1)多项式乘以多项式,结果仍是多项式,在合并同类项前,积的项数为两个多项式的项数的积,通过这个方法检验是否“重乘”或“漏乘”;(2)相乘时注意符号问题,多项式中的每一项都包含它前面的符号;(3)结果中若有同类项,则要合并同类项,使结果最简.
2.下列各式计算正确的是(　　)A.(x+5)(x-5)=x2-10x+25B.(2x+3)(x-3)=2x2-9C.(3x+2)(3x-1)=9x2+3x-2D.(x-1)(x+7)=x2-6x-7
2.C　(x+5)(x-5)=x2-5x+5x-25=x2-25,A选项错误;(2x+3)(x-3)=2x2-6x+3x-9=2x2-3x-9,B选项错误;(3x+2)·(3x-1)=9x2-3x+6x-2=9x2+3x-2,C选项正确;(x-1)(x+7)=x2+7x-x-7=x2+6x-7,D选项错误.
3.[2021安徽阜阳期末]观察下列两个多项式相乘的运算过程:  根据你发现的规律,若(x+a)(x+b)=x2-7x+12,则a,b的值可能分别是(　　)A.-3,-4B.-3,4C.3,-4D.3,4
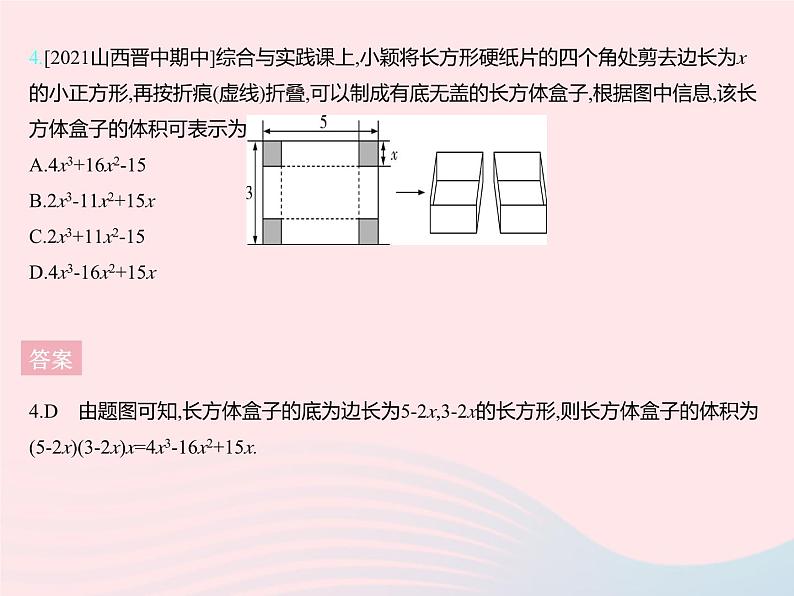
4.[2021山西晋中期中]综合与实践课上,小颖将长方形硬纸片的四个角处剪去边长为x的小正方形,再按折痕(虚线)折叠,可以制成有底无盖的长方体盒子,根据图中信息,该长方体盒子的体积可表示为(　　) A.4x3+16x2-15B.2x3-11x2+15xC.2x3+11x2-15D.4x3-16x2+15x
4.D　由题图可知,长方体盒子的底为边长为5-2x,3-2x的长方形,则长方体盒子的体积为(5-2x)(3-2x)x=4x3-16x2+15x.
5.[2020江苏无锡月考]设A=(x-3)(x-7),B=(x-2)(x-8),则A,B的大小关系为　　　　. 
5.A>B　∵A=(x-3)(x-7)=x2-10x+21,B=(x-2)(x-8)=x2-10x+16,∴A-B=x2-10x+21-(x2-10x+16)=5>0,∴A>B.
6.计算:(1)(2x-5y)(3x-y);(2)(x-y)(x2+xy+y2);(3)[2021重庆中考A卷](x-y)2+x(x+2y);(4)(a+b+c)(a-b+c).
6.解:(1)(2x-5y)(3x-y)=6x2-2xy-15xy+5y2=6x2-17xy+5y2.(2)(x-y)(x2+xy+y2)=x3+x2y+xy2-x2y-xy2-y3=x3-y3.(3)(x-y)2+x(x+2y)=(x-y)(x-y)+x(x+2y)=x2-xy-xy+y2+x2+2xy=2x2+y2.(4)(a+b+c)(a-b+c)=a2-ab+ac+ab-b2+bc+ac-bc+c2=a2-b2+c2+2ac.
7.解方程:(3x-1)(2x-3)=(6x-5)(x-2)+5.
7.解:去括号,得6x2-9x-2x+3=6x2-12x-5x+10+5,移项,合并同类项,得6x=12,将未知数系数化为1,得x=2.
8.先化简,再求值:(x-2y)(x+4y)-(2x-y)(x+y),其中x=-2,y=3.
8.解:(x-2y)(x+4y)-(2x-y)(x+y)=x2+4xy-2xy-8y2-(2x2+2xy-xy-y2)=x2+4xy-2xy-8y2-2x2-2xy+xy+y2=-x2+xy-7y2,当x=-2,y=3时,原式=-(-2)2+(-2)×3-7×32=-73.
1.[2020广西玉林期末]已知a+b=4,ab=3,则代数式(a+2)(b+2)的值是(　　)　　　　　 　　　　　　　　　　A.7B.9C.11D.15
1.D　(a+2)(b+2)=ab+2a+2b+4=ab+2(a+b)+4.∵a+b=4,ab=3,∴原式=3+2×4+4=3+8+4=15.
2.已知(1+x)(2x2+ax+1)的结果中x2项的系数为-2,则a的值为(　　)A.-2B.1C.-4D.2
2.C　(1+x)(2x2+ax+1)=2x3+(a+2)x2+(a+1)x+1,由结果中x2项的系数为-2,得a+2=-2,解得a=-4.
3.[2021河北保定期中]现有若干张卡片,分别是正方形卡片A,B和长方形卡片C,卡片大小如图所示.若要用这三种卡片拼一个长为4a+b、宽为a+2b的大长方形,则需要C类卡片　　　　张. 
3.9　长为4a+b、宽为a+2b的长方形的面积为(4a+b)(a+2b)=4a2+9ab+2b2,∵A类卡片的面积为a2,B类卡片的面积为b2,C类卡片的面积为ab,∴需要A类卡片4张,B类卡片2张,C类卡片9张.
利用多项式乘多项式的运算法则求出大长方形的面积,再结合正方形、长方形的面积确定每类卡片所需要的张数.
4.已知x2-5x=14,则(x-1)(2x-1)-(x+1)2+1的值为　　　　. 
4.15　(x-1)(2x-1)-(x+1)2+1=2x2-x-2x+1-(x2+x+x+1)+1=x2-5x+1,因为x2-5x=14,所以原式=14+1=15.
6.如图1,长方形的两边长分别为m+3,m+13,面积为S1;如图2,长方形的两边长分别为m+5,m+7,面积为S2.(其中m为正整数) (1)S1　　　　S2;(填“>”“<”或“=”) (2)若某个图形的面积介于S1,S2之间(不包括S1,S2)且为整数,这样的整数值有且只有19个,则m的值为　　　　. 
6.(1)>;(2)4(1)S1=(m+13)(m+3)=m2+16m+39,S2=(m+7)(m+5)=m2+12m+35,得S1-S2=4m+4,∵m为正整数,∴4m+4>0,S1>S2.(2)由题意得4m+4=20,m=4.
7.[2021河北唐山期末]欢欢和乐乐两人共同计算一道整式乘法题:(2x+a)(3x+b).欢欢由于把第一个多项式中a的符号抄成了负号,所以得到的结果为6x2-13x+6,乐乐由于漏抄了第二个多项式中x的系数,所以得到的结果为2x2-x-6.(1)求式子中a,b的值.(2)请你计算出这道整式乘法题的正确答案.
7.解:(1)因为欢欢把第一个多项式中a的符号抄成了负号,且得到的结果为6x2-13x+6,所以(2x-a)(3x+b)=6x2+(2b-3a)x-ab=6x2-13x+6,可得2b-3a=-13①.因为乐乐漏抄了第二个多项式中x的系数,且得到的结果为2x2-x-6,所以(2x+a)(x+b)=2x2+(2b+a)x+ab=2x2-x-6,可得2b+a=-1②.联立①②可解得a=3,b=-2.(2)由(1)知正确的式子为(2x+3)(3x-2),(2x+3)(3x-2)=6x2+5x-6.
素养提升8.你能化简(a-1)(a99+a98+a97+‧‧‧+a2+a+1)吗?我们不妨先从简单情况入手,发现规律,归纳结论.(1)先填空:(a-1)(a+1)=　　　　;(a-1)(a2+a+1)=　　　　;(a-1)(a3+a2+a+1)=　　　　‧‧‧‧‧‧由此猜想(a-1)(a99+a98+a97+‧‧‧+a2+a+1)=　　　　. (2)利用这个结论,你能解决下面两个问题吗?①求2199+2198+2197+‧‧‧+22+2+1的值;②若a5+a4+a3+a2+a+1=0,则a6等于多少?
8.解:(1)a2-1　a3-1　a4-1　a100-1(2)①利用结论:(2-1)×(2199+2198+2197+‧‧‧+22+2+1)=2200-1,因为2-1=1,所以2199+2198+2197+‧‧‧+22+2+1=2200-1.②利用结论:(a-1)(a5+a4+a3+a2+a+1)=a6-1,所以a6-1=0,所以a6=1.