




还剩7页未读,
继续阅读
成套系列资料,整套一键下载
2023七年级数学下册第九章三角形易错疑难集训上课课件新版冀教版
展开
这是一份2023七年级数学下册第九章三角形易错疑难集训上课课件新版冀教版,共13页。
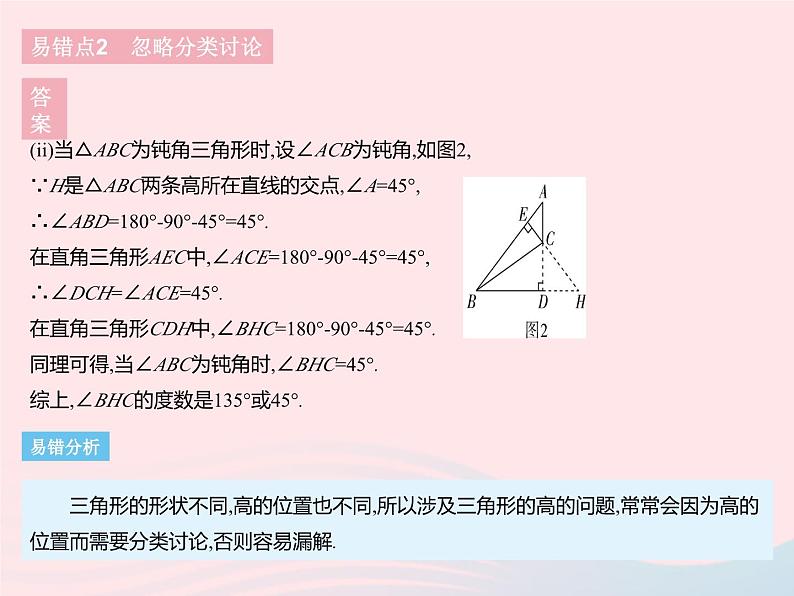
易错疑难集训1.将一条长为16 cm的细绳围成一个等腰三角形,若其中一边长为4 cm,则该等腰三角形的腰长为( )A.4 cm B.6 cmC.4 cm或6 cm D.4 cm或8 cm易错点1 等腰三角形的三边关系答案 2.已知非直角三角形ABC中,∠A=45°,高BD和CE所在直线交于点H,求∠BHC的度数.易错点2 忽略分类讨论答案2.解:三角形的形状不同,高的交点的位置也不同.非直角三角形的高所在直线的交点可能在三角形内部,也可能在三角形外部,故应分两种情况讨论.(i)当△ABC为锐角三角形时,如图1,∵BD,CE是△ABC的高,∠A=45°, ∴∠ADB=∠BEH=90°.在△ABD中,∠ABD=180°-90°-45°=45°.∵∠BHC是△BHE的一个外角, ∴∠BHC=90°+45°=135°.易错点2 忽略分类讨论答案(ii)当△ABC为钝角三角形时,设∠ACB为钝角,如图2,∵H是△ABC两条高所在直线的交点,∠A=45°,∴∠ABD=180°-90°-45°=45°.在直角三角形AEC中,∠ACE=180°-90°-45°=45°,∴∠DCH=∠ACE=45°.在直角三角形CDH中,∠BHC=180°-90°-45°=45°.同理可得,当∠ABC为钝角时,∠BHC=45°.综上,∠BHC的度数是135°或45°. 三角形的形状不同,高的位置也不同,所以涉及三角形的高的问题,常常会因为高的位置而需要分类讨论,否则容易漏解.易错分析3.在等腰三角形中,一腰上的中线把它的周长分为15 cm和12 cm两部分,求这个三角形各边的长.易错点2 忽略分类讨论答案 易错点2 忽略分类讨论答案 由于等腰三角形的底边长和腰长还没确定,所以解题时需要分类讨论,否则容易漏解.易错分析1.如图,在△ABC中,AB=AC,P是底边BC上的任意一点(不与点B,C重合),CD⊥AB于点D,PE⊥AB于点E,PF⊥AC于点F.请对CD=PE+PF进行说明.疑难点1 三角形的高与面积答案 等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高.归纳总结2.[2021河北沧州期末]如图1,△ABC中,BO,CO分别平分∠ABC,∠ACB,O为BO与CO的交点.(1)问题解决若图1中∠A=62°,求∠BOC的度数.(写出求解过程)(2)拓展与探究①请探究图1中∠BOC与∠A的关系;②如图2,BO,CO分别是∠ABC和∠ACB的外角∠CBD,∠BCE的平分线,O为BO与CO的交点,请探究∠BOC与∠A的关系;③如图3,BO,CO分别平分∠ABC,∠ACE,O为BO与CO的交点,则∠BOC与∠A的关系是 .(请直接写出你的结论) 疑难点2 类比思想的运用疑难点2 类比思想的运用答案 疑难点2 类比思想的运用答案 疑难点2 类比思想的运用答案
易错疑难集训1.将一条长为16 cm的细绳围成一个等腰三角形,若其中一边长为4 cm,则该等腰三角形的腰长为( )A.4 cm B.6 cmC.4 cm或6 cm D.4 cm或8 cm易错点1 等腰三角形的三边关系答案 2.已知非直角三角形ABC中,∠A=45°,高BD和CE所在直线交于点H,求∠BHC的度数.易错点2 忽略分类讨论答案2.解:三角形的形状不同,高的交点的位置也不同.非直角三角形的高所在直线的交点可能在三角形内部,也可能在三角形外部,故应分两种情况讨论.(i)当△ABC为锐角三角形时,如图1,∵BD,CE是△ABC的高,∠A=45°, ∴∠ADB=∠BEH=90°.在△ABD中,∠ABD=180°-90°-45°=45°.∵∠BHC是△BHE的一个外角, ∴∠BHC=90°+45°=135°.易错点2 忽略分类讨论答案(ii)当△ABC为钝角三角形时,设∠ACB为钝角,如图2,∵H是△ABC两条高所在直线的交点,∠A=45°,∴∠ABD=180°-90°-45°=45°.在直角三角形AEC中,∠ACE=180°-90°-45°=45°,∴∠DCH=∠ACE=45°.在直角三角形CDH中,∠BHC=180°-90°-45°=45°.同理可得,当∠ABC为钝角时,∠BHC=45°.综上,∠BHC的度数是135°或45°. 三角形的形状不同,高的位置也不同,所以涉及三角形的高的问题,常常会因为高的位置而需要分类讨论,否则容易漏解.易错分析3.在等腰三角形中,一腰上的中线把它的周长分为15 cm和12 cm两部分,求这个三角形各边的长.易错点2 忽略分类讨论答案 易错点2 忽略分类讨论答案 由于等腰三角形的底边长和腰长还没确定,所以解题时需要分类讨论,否则容易漏解.易错分析1.如图,在△ABC中,AB=AC,P是底边BC上的任意一点(不与点B,C重合),CD⊥AB于点D,PE⊥AB于点E,PF⊥AC于点F.请对CD=PE+PF进行说明.疑难点1 三角形的高与面积答案 等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高.归纳总结2.[2021河北沧州期末]如图1,△ABC中,BO,CO分别平分∠ABC,∠ACB,O为BO与CO的交点.(1)问题解决若图1中∠A=62°,求∠BOC的度数.(写出求解过程)(2)拓展与探究①请探究图1中∠BOC与∠A的关系;②如图2,BO,CO分别是∠ABC和∠ACB的外角∠CBD,∠BCE的平分线,O为BO与CO的交点,请探究∠BOC与∠A的关系;③如图3,BO,CO分别平分∠ABC,∠ACE,O为BO与CO的交点,则∠BOC与∠A的关系是 .(请直接写出你的结论) 疑难点2 类比思想的运用疑难点2 类比思想的运用答案 疑难点2 类比思想的运用答案 疑难点2 类比思想的运用答案
相关资料
更多









