人教版七年级数学上册单元检测 第三章

第三章综合

一、选择题(每题3分，共30分)

1．下列四个式子中，是一元一次方程的是(　　)

A．1＋2＋3＋4＝10 

B．2x－3 

C.＝＋1 

D．x＋3＝y

2．【2023·天津和平区模拟】下列等式变形中，正确的是(　　)

A．若a＝b，则a－3＝3－b 

B．若＝，则x＝y

C．若ac＝bc，则a＝b     

D．若＝，则b＝d

3．【母题：教材P83习题T3】方程－2x＋3＝7的解是(　　)

A．x＝5  B．x＝4  C．x＝3.5  D．x＝－2

4．下列方程的变形中，正确的是(　　)

A．将方程3x－5＝x＋1移项，得3x－x＝1－5

B．将方程－15x＝5两边同除以－15，得x＝－3

C．将方程2(x－1)＋4＝x去括号，得2x－2＋4＝x

D．将方程＋＝1去分母，得4x＋3y＝1

5．设P＝2y－2，Q＝2y＋3，且3P－Q＝1，则y的值是(　　)

A．0.4  B．2.5  C．－0.4  D．－2.5

6．【2023·北京顺义区模拟】若关于x的方程＝1的解为x＝2，则m的值是(　　)

A．2.5  B．1  C．－1  D．3

7．已知方程7x＋2＝3x－6与关于x的方程x－1＝k的解相同，则3k2－1的值为(　　)

A．18  B．20  C．26  D．－26

8．【数学文化】【2022·十堰】我国古代数学名著《张邱建算经》中记载：“今有清酒一斗直粟十斗，醑酒一斗直粟三斗，今持粟三斛，得酒五斗，问清、醑酒各几何？”意思是：现在一斗清酒价值10斗谷子，一斗醑酒价值3斗谷子，现在拿30斗谷子，共换了5斗酒，问清、醑酒各几斗？如果设清酒x斗，那么可列方程为(　　)

A．10x＋3(5－x)＝30  B．3x＋10(5－x)＝30 

C.＋＝5  D.＋＝5

9．方程－＝1中有一个数被墨水盖住了，看答案知道，这个方程的解是x＝－1，那么被墨水盖住的数是(　　)

A．  B．1  C．－  D．0

10．现有m辆客车、n个人．若每辆客车乘40人，则还有10人不能上车；若每辆客车乘43人，则只有1人不能上车．据此列出下列四个等式：①40m＋10＝43m－1；②＝；③＝；④40m＋10＝43m＋1.其中正确的是(　　)

A．①②  B．②④  C．②③  D．③④

二、填空题(每题3分，共24分)

11．已知(m－4)x|m|－3＋2＝0是关于x的一元一次方程，则m的值为________．

12．若－0.2a3x＋4b3与aby是同类项，则xy＝________．

13．已知y＝3是关于y的方程ay＝－6的解，那么关于x的方程4(x－a)＝a－(x－6)的解是____________．

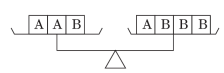
14．【母题：教材P81图3.1－2】如图，标有相同字母的物体的质量相同，若A的质量为20 g，当天平处于平衡状态时，B的质量为________．

15．【新考法】如果规定“*”的意义为：a*b＝(其中a，b为有理数)，那么方程3*x＝的解是________．

16．甲、乙两个足球队进行对抗赛，规定胜一场得3分，平一场得1分，负一场得0分．两队一共比赛了10场，甲队保持不败，得22分．甲队胜________场．

17．在国家“双减”政策出台后，同学们的课余生活更加丰富了，为迎接元旦活动，美术兴趣小组要完成学校布置的剪纸作品任务，若每人剪5个，则可比计划多剪9个；若每人剪4个，则将比计划少剪15个，求这批剪纸作品任务共多少个．若设美术兴趣小组共有x人，则这个方程可以列为_____________________．

18．【2022·河北】如图，棋盘旁有甲、乙两个围棋盒．

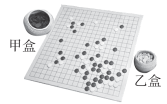
(1)若甲盒中都是黑子，共10个，乙盒中都是白子，共8个．嘉嘉从甲盒拿出a个黑子放入乙盒，使乙盒棋子总数是甲盒所剩棋子数的2倍，则a＝________；

(2)若甲盒中都是黑子，共m(m＞2)个，乙盒中都是白子，共2m个，嘉嘉从甲盒拿出a(1＜a＜m)个黑子放入乙盒中，此时乙盒棋子总数比甲盒所剩棋子数多________个；接下来，嘉嘉又从乙盒拿回a个棋子放到甲盒，其中含有x(0＜x＜a)个白子，此时乙盒中有y个黑子，则的值为________．

三、解答题(19，23，24题每题12分，其余每题10分，共66分)

19．【母题：教材P111复习题T2】解下列方程：

(1)5y－3＝2y＋6；　　　　　　　　　　　(2)2(x－2)－3(4x－1)＝5(1－x)；

(3)－＝2－；             (4)－＝.

20．当m为何值时，关于x的方程5m＋3x＝1＋x的解比关于x的方程2x－1＝3x＋1的解大3?

21．下面是小红解方程－＝1的过程：

解：去分母，得2(2x＋1)－5x－1＝1.①

去括号，得4x＋2－5x－1＝1.②

移项，得4x－5x＝1－2＋1.③

合并同类项，得－x＝0.④

系数化为1，得x＝0.⑤

上述解方程的过程中，是否有错误？

答：________(填“有”或者“没有”)；如果有错误，则开始出错的一步是________(填序号)．如果上述解方程的过程有错误，请你给出正确的过程．

22．【母题：教材P91习题T7】如图，一块长5厘米、宽2厘米的长方形纸板，一块长4厘米、宽1厘米的长方形纸板，与一块正方形纸板以及另两块长方形纸板，恰好拼成一个大正方形．大正方形的面积是多少？

23．【2022·海南】某省某村委会根据“十四五”规划的要求，打造乡村品牌，推销有机黑胡椒和有机白胡椒．已知每千克有机黑胡椒比每千克有机白胡椒的售价便宜10元，购买2千克有机黑胡椒和3千克有机白胡椒需付280元，求每千克有机黑胡椒和每千克有机白胡椒的售价．

24．某市中小学统一组织文艺汇演，甲、乙两所学校共92人(其中甲校人数多于乙校人数，且甲校人数不超过90人)准备统一购买服装参加演出．下面是某服装厂给出的演出服装的价格表：

如果两校单独购买服装，一共应付5 000元．

(1)如果甲、乙两校联合起来购买服装，那么比各自购买服装共可以节省多少钱？

(2)甲、乙两校分别有多少人准备参加演出？

(3)如果甲校有10名同学要去参加书法绘画比赛，不能参加演出，请为两校设计一种最省钱的购买服装方案．

答案

一、1.C　【点拨】A中式子没有未知数，错误；B中式子不是等式，错误；C中式子满足一元一次方程的定义，正确；D中式子有两个未知数，错误．故选C.

2．B　【点拨】若a＝b，则a－3＝b－3，A错误；若＝，则×a＝×a，x＝y，B正确；若ac＝bc，当c≠0时，a＝b，当c＝0时，a＝b不一定成立，C错误；若＝，则bc＝ad，推不出b＝d，D错误．故选B.

3．D　【点拨】－2x＋3＝7，移项、合并同类项，得－2x＝4，系数化为1，得x＝－2，故选D.

4．C　【点拨】3x－5＝x＋1，移项，得3x－x＝1＋5，A错误；

－15x＝5，系数化为1，得x＝－，B错误；

2(x－1)＋4＝x，去括号，得2x－2＋4＝x，C正确；

＋＝1，去分母，得4x＋3y＝12，D错误．故选C.

5．B　【点拨】3P－Q＝3(2y－2)－(2y＋3)＝4y－9＝1，解得y＝2.5，故选B.

6．B　【点拨】根据题意得 ＝1，解得m＝1，故选B.

7．C　【点拨】7x＋2＝3x－6，解得x＝－2，则－2－1＝k，k＝－3, 3k2－1＝

3×9－1＝26，故选C.

8．A　【点拨】根据换清酒所用的谷子斗数＋换醑酒所用的谷子斗数＝30斗列

方程．

9． B　【点拨】设墨水盖住的数为a，由方程的解是x＝－1，得－＝1，化简得＝－1，解得a＝1，故选B.

10．D　【点拨】由题意得40m＋10＝n，43m＋1＝n，则40m＋10＝43m＋1，①错④对；m＝＝，②错③对，故选D.

二、11.－4　【点拨】由题意得m－4≠0，|m|－3＝1，解得m＝－4.

12．－3　【点拨】由题意得3x＋4＝1，3＝y，解得x＝－1，y＝3，则xy＝－3.

13．x＝－　【点拨】将y＝3代入ay＝－6，解得a＝－2.再将a＝－2代入4(x－a)＝a－(x－6)求解即可．

14．10 g　【点拨】设B的质量为x g，根据题意得2×20＋x＝20＋3x，解得x＝10，所以B的质量为10 g.

15．x＝1　【点拨】由题意得3*x＝＝，解得x＝1.

16．6　【点拨】设甲队胜x场，则平(10－x)场，根据题意得3x＋(10－x)＝22.解得x＝6，即甲队胜6场．

17．5x－9＝4x＋15

18．(1)4　(2)(m＋2a)；1　【点拨】(1)根据题意可列方程2(10－a)＝8＋a，解得a＝4.

(2)根据题意得 2m＋a－(m－a)＝m＋2a(个)．

接下来，嘉嘉又从乙盒拿回a个棋子放到甲盒中，这a个棋子中有x个白子，(a－x)个黑子，则a－(a－x)＝y.即x＝y，则＝1.

三、19.【解】(1)移项，得5y－2y＝6＋3.

合并同类项，得3y＝9.

系数化为1，得y＝3；

(2)去括号，得2x－4－12x＋3＝5－5x，

移项，得2x－12x＋5x＝5＋4－3，

合并同类项，得－5x＝6，

系数化为1，得x＝－；

(3)去分母，得4(7x－1)－6(5x＋1)＝2×12－3(3x＋2)，

去括号，得28x－4－30x－6＝24－9x－6，

移项，得28x－30x＋9x＝24＋6＋4－6，

合并同类项，得7x＝28，

系数化为1，得x＝4；

(4)原方程可化为－＝.

去分母，得40x－(16－30x)＝2(31x＋8)．

去括号，得40x－16＋30x＝62x＋16.

移项，得40x＋30x－62x＝16＋16.

合并同类项，得8x＝32.

系数化为1，得x＝4.

20．【解】解方程2x－1＝3x＋1，得x＝－2，

由题意，得方程5m＋3x＝1＋x的解是x＝－2＋3＝1，

把x＝1代入5m＋3x＝1＋x中，解得m＝－.

21．【解】有；①

正确的过程如下：

去分母，得2(2x＋1)－(5x－1)＝6.

去括号，得4x＋2－5x＋1＝6.

移项，得4x－5x＝6－2－1.

合并同类项，得－x＝3.

系数化为1，得x＝－3.

22．【解】设大正方形的边长为x厘米，

由题图可得x－2－1＝4＋5－x，

解得x＝6，

则6×6＝36(平方厘米)．

所以大正方形的面积为36平方厘米．

23．【解】设每千克有机黑胡椒的售价为x元，每千克有机白胡椒的售价为

(10＋x)元，

依题意，得2x＋3(10＋x)＝280.

解得x＝50.

则10＋x＝60.

答：每千克有机黑胡椒的售价为50元，每千克有机白胡椒的售价为60元．

24．【解】(1)由题意得5 000－92×40＝1 320(元)．

答：甲、乙两校联合起来购买服装，比各自购买服装共可以节省1 320元．

(2)设甲校有x人准备参加演出，则乙校有(92－x)人准备参加演出．

由题意，得50x＋60(92－x)＝5 000，

解得x＝52，

则92－x＝40.

答：甲、乙两校分别有52人、40人准备参加演出．

(3)因为甲校有10人不能参加演出，

所以甲校有52－10＝42(人)参加演出，则两校参加演出的人数为42＋40＝82(人)．

若两校联合购买82套服装，则需要

50×82＝4 100(元)，

但如果两校联合购买91套服装，只需40×91＝3 640(元)，

3 640<4 100，

因此，最省钱的购买服装方案是两校联合购买91套服装(即比实际人数多购买9套)．