人教版七年级数学上册单元检测 第四章

第四章综合

一、选择题(每题3分，共30分)

1．下列各组图形中，都是平面图形的是(　　)

A．三角形、圆、球、圆锥        B．长方体、正方体、圆柱、球

C．长方形、三角形、正方形、圆  D．扇形、长方形、三棱柱、圆锥

2．【2022·永州】我市江华县有“神州瑶都”的美称，每逢“盘王节”会表演长鼓舞，长鼓舞中使用的“长鼓”内腔挖空，两端相通，两端鼓口为圆形，中间鼓腰较为细小，如图为类似“长鼓”的几何体，其从上面看得到的平面图形的大致形状是(　　)

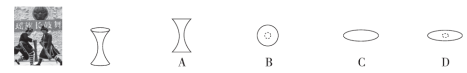
3．下列说法中，正确的是(　　)

A．两点确定一条直线  B．两条射线组成的图形叫做角

C．两点之间直线最短  D．若AB＝BC，则点B为AC的中点

4．若∠A＝40°，则∠A的余角为(　　)

A．30°  B．40°  C．50°  D．140°

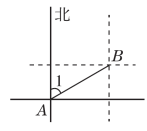
5．【母题：教材P140习题T12】如图，∠1＝60°，则点A在点B的(　　)

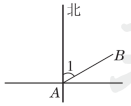A．北偏东60° 

B．南偏东60°

C．南偏西60° 

D．南偏西30°

6．【2023·清华附中模拟】已知线段AB＝15 cm，点C是直线AB上一点，BC＝5 cm，若M是AC的中点，N是BC的中点，则线段MN的长度是(　　)

A．10 cm  B．5 cm  C．10 cm或5 cm  D．7.5 cm

7．已知∠1＝28°24′，∠2＝28.24°，∠3＝28.4°，则下列说法中，正确的是(　　)

A．∠1＝∠2＜∠3  B．∠1＝∠3＞∠2 

C．∠1＜∠2＝∠3  D．∠1＝∠2＞∠3

8．【母题：教材P134练习T1】钟表在8：25时，时针与分针夹角的度数是(　　)

A．101.5°  B．102.5°  C．120°  D．125°

9．【2022·枣庄】某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“亮”字所在面相对的面上的汉字是(　　)

A．青  B．春  C．梦  D．想

10．【2022·齐齐哈尔】由一些大小相同的小正方体搭成的几何体从三个角度看得到的平面图形都是如图所示的“田”字形，则搭成该几何体的小正方体的个数最少为(　　)

A．4个  B．5个  C．6个  D．7个

二、填空题(每题3分，共24分)

11．【2023·西工大附中月考】七棱柱有________个面，________个顶点．

12．在校园中的一条大路两旁种植树木(树木种在一条直线上)，确定了两棵树的位置就能确定一排树的位置，这利用了我们所学过的数学知识是______________________．

13．【母题：教材P130习题T12】三条直线两两相交，最少有______个交点，最多有______个交点．

14．笔尖在纸上快速滑动写出了一个又一个字，这说明了______________；钟表的时针和分针旋转一周，均形成一个圆面，这说明了______________．(从点、线、面的角度作答)

15．【母题：教材P128练习T3】如图，点D是线段AB的中点，点C是线段AD的中点，若CD＝1，则AB＝________．

16．如图，点A，O，B在一条直线上，且∠AOC＝50°，OD平分∠AOC，则∠BOD＝________．

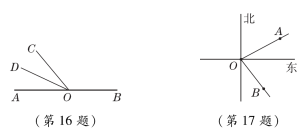
17．如图，某海域有A，B，O三个小岛，在小岛O处观测到小岛A在其北偏东62°的方向上，观测到小岛B在其南偏东38°12′的方向上，则∠AOB的补角等于________．

18．往返于甲、乙两地的客车，中途停靠5个车站(来回票价一样)，且任意两站之间的票价都不同，共有________种不同的票价，需准备________种车票．

三、解答题(19～21题每题10分，其余每题12分，共66分)

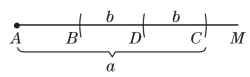
19．已知线段a，b，利用尺规，求作一条线段AB，使AB＝a－2b.(不写作法，保留作图痕迹)

20．点A，B，C，D的位置如图，按下列要求画出图形：

(1)画直线AB，直线CD，它们相交于点E；

(2)连接AC，连接BD，它们相交于点O；

(3)画射线AD，射线BC，它们相交于点F.

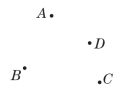
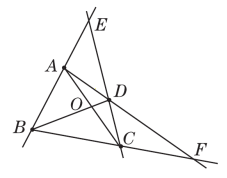
21．【母题：教材P128练习T3】如图，已知线段AB＝4.8 cm，点M为AB的中点，点P在MB上，N为PB的中点，且NB＝0.8 cm，求AP的长．

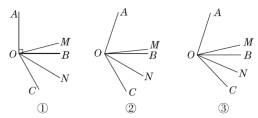
22．如图，射线OA的方向是北偏东15°，射线OB的方向是北偏西40°，∠AOB＝∠AOC，射线OD是OB的反向延长线．

(1)射线OC的方向是____________；

(2)若射线OE平分∠COD，求∠AOE的度数．

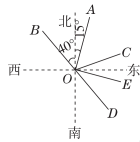
23．如图是某种长方体产品的展开图，高为3 cm.

(1)求每件这种产品的体积；

(2)请为厂家设计一种包装纸箱，使每箱能装5件这种产品，要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计，纸箱的表面积尽可能小)，求此包装纸箱的表面积．

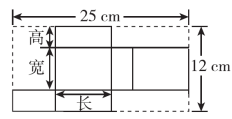
24．如图，OM是∠AOC的平分线，ON是∠BOC的平分线．

(1)如图①，当∠AOB是直角，∠BOC＝60°时，∠MON的度数是多少？

(2)如图②，当∠AOB＝α，∠BOC＝60°时，猜想∠MON与α的数量关系．

(3)如图③，当∠AOB＝α，∠BOC＝β(0°＜α＋β＜180°)时，猜想∠MON与α，β的数量关系，并说明理由．

答案

一、1.C　【点拨】平面图形有三角形，圆，长方形，正方形，扇形等；立体图形有球，圆锥，长方体，正方体，圆柱，三棱柱等，则C中全是平面图形，故选C.

2．B

3．A　【点拨】两点确定一条直线，A正确；由同一个点射出的两条射线组成的图形叫做角，B错误；两点之间线段最短，C错误；若AB＝BC，B有可能是AC的中点，也有可能A，B，C不在同一条直线上，如图，D错误．故选A.

4．C　【点拨】∠A＝40°，∠A的余角为90°－40°＝50°，故选C.

5．C　【点拨】如图，∠1＝60°，所以点A在点B的南偏西60°，故选C.

6．D　【点拨】如图①，MN＝＋＝7.5(cm)；如图②，MN＝－＝7.5(cm)．故选D.

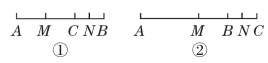
7．B　【点拨】＝0.4°，所以∠1＝28.4°＝∠3>∠2，故选B.

8．B　【点拨】时针与分针的夹角是×3＋×＝102.5°，故选B.

9．D　【点拨】把展开图还原成正方体可知，“点”对“春”，“青”对“梦”，“亮”对“想”，故选D.

10．C　【点拨】从上面看知最下面一层一定有四个小正方体，从正面看和左面看知上面一层至少有处在对角的位置上的两个小正方体，故搭成该几何体的小正方体的个数最少为6个．

二、11.9；14　【点拨】七棱柱有7个侧面，2个底面，共9个面，7＋7＝14(个)顶点．

12．两点确定一条直线　

13．1；3　【点拨】如图①，最少有1个交点；如图②，最多有3个交点．

14．点动成线；线动成面　【点拨】笔尖为一个点，写出了字，说明了点动成线；时针和分针为线，旋转形成了圆面，说明了线动成面．

15．4　【点拨】因为点C是线段AD的中点，所以AD＝2CD＝2.因为点D是线段AB的中点，所以AB＝2AD＝4.

16．155°　【点拨】因为OD平分∠AOC，所以∠BOD＝∠AOB－∠AOD＝∠AOB－∠AOC＝180°－＝155°.

17．100°12′　【点拨】由题图可知∠AOB的补角为180°－∠AOB＝62°＋38°12′＝100°12′.

18．21；42　【点拨】如图，甲、乙两地的车站分别用A、G表示，中途的五个车站分别用B，C，D，E，F表示，用AB表示起点为A，终点为B的车票票价，故有以下不同票价：AB，AC，AD，AE，AF，AG，BC，BD，BE，BF，BG，CD，CE，CF，CG，DE，DF，DG，EF，EG，FG，共21种，来回车票不同，则需准备21×2＝42(种)车票．

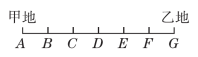
三、19.【解】如图，线段AB就是所求的线段．

20．【解】如图．

21．【解】方法一　因为N为PB的中点，

所以PB＝2NB.

又知NB＝0.8 cm，

所以PB＝2×0.8＝1.6(cm)．

所以AP＝AB－PB＝4.8－1.6＝3.2(cm)．

方法二　因为N是PB的中点，

所以PB＝2NB.

而NB＝0.8 cm，所以PB＝2×0.8＝1.6(cm)．

因为M为AB的中点，所以AM＝MB＝AB.

而AB＝4.8 cm，

所以AM＝BM＝2.4 cm.

又因为MP＝MB－PB＝2.4－1.6＝0.8(cm)，

所以AP＝AM＋MP＝2.4＋0.8＝3.2(cm)．

【点拨】(1)把一条线段分成两条相等线段的点，叫做这条线段的中点．

(2)线段中点的表达形式有三种. 若点C是线段AB的中点，则①AC＝BC；②AB＝2AC＝2BC；③AC＝BC＝AB.熟悉它的表达形式对以后学习几何的推理论证有帮助．

22．【解】(1)北偏东70°

(2)因为∠AOB＝40°＋15°＝55°，∠AOB＝∠AOC，

所以∠AOC＝55°，

所以∠BOC＝110°.

又因为射线OD是OB的反向延长线，

所以∠BOD＝180°.

所以∠COD＝180°－110°＝70°.

又因为OE平分∠COD，

所以∠COE＝35°.

又因为∠AOC＝55°，

所以∠AOE＝55°＋35°＝90°.

23．【解】(1)长方体的高为3 cm，则长方体的宽为12－2×3＝6(cm)，长为×(25－

3－6)＝8(cm)．根据题意，可得每件这种产品的体积为8×6×3＝144(cm3)．

(2)因为该产品的高为3 cm，宽为6 cm，长为8 cm，所以装5件这种产品，要使纸箱所用的材料尽可能少，应该尽量使6 cm×8 cm的面重叠在一起，所以用规格为15 cm×6 cm×8 cm的包装纸箱符合要求．所以包装纸箱的表面积为2×(8×6＋8×15＋6×15)＝516(cm2)．

【点拨】利用展开图求立体图形的表面积或体积时要把握两个关键：一是平面图形与立体图形之间的关系， 二是展开图中的数据与原立体图形的数据之间的关系．

24．【解】(1)∠MON＝∠MOC－∠NOC＝∠AOC－∠BOC＝(∠AOC－∠BOC)＝∠AOB＝45°.

(2)∠MON＝∠MOC－∠NOC＝∠AOC－∠BOC＝(∠AOC－∠BOC)＝∠AOB＝α.

(3)∠MON＝α.理由：∠MON＝∠MOC－∠NOC＝·(α＋β)－β＝α.