人教版七年级数学上册 期末综合素质评价

期末综合

一、选择题(每题3分，共30分)

1．【数学文化】在《九章算术注》中用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(白色为正，灰色为负)，如图①表示的是＋21－32＝－11的计算过程，则图②表示的过程是在计算(　　)

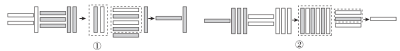
A．(－13)＋(＋23)＝10  B．(－31)＋(＋32)＝1 

C．(＋13)＋(＋23)＝36  D．(＋13)＋(－23)＝－10

2．下列运算中，正确的是(　　)

A．－2－1＝－1  B．－2(x－3y)＝－2x＋3y

C．3÷6×＝3÷3＝1  D．5x2－2x2＝3x2

3．过度包装既浪费资源又污染环境，据测算如果全国每年减少十分之一的包装纸用量，那么能减少3.12×106吨二氧化碳的排放量，把3.12×106写成原数是(　　)

A．312 000  B．3 120 000  C．31 200 000  D．312 000 000

4．若A＝x2－xy，B＝xy＋y2，则3A－2B＝(　　)

A．3x2－2y2－5xy  B．3x2－2y2  C．－5xy  D．3x2＋2y2

5．【2023·成都温江区模拟】已知－7是关于x的方程2x－7＝ax的解，则式子a－的值是(　　)

A．1  B．2  C．3  D．4

6．【母题：教材P117探究】如图所示的几何体从正面看到的图形是(　　)

7．【2023·重庆南岸区模拟】若方程(m2－1)x2－mx－x＋2＝0是关于x的一元一次方程，则式子|m－1|的值为(　　)

A．0  B．2  C．0或2  D．－2

8．如图，点C是线段AB上的一点，且AC＝2BC.下列结论，正确的是(　　)

A．BC＝AB  B．AC＝AB  C．BC＝AB  D．BC＝AC

9．下列说法：①若点C是AB的中点，则AC＝BC；②若AC＝BC，则点C是AB的中点；③若OC是∠AOB的平分线，则∠AOC＝∠AOB；④若∠AOC＝∠AOB，则OC是∠AOB的平分线．其中正确的有(　　)

A．1个  B．2个  C．3个  D．4个

10．【数学文化】中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初日健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是：有人要去某关口，路程为378里，第一天健步行走，从第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地．则此人第三天走的路程为(　　)

A．96里  B．48里  C．24里  D．12里

二、填空题(每题3分，共24分)

11．用一个钉子把一根木条钉在木板上，用手拨木条，木条能转动，这说明______________________________________________________________；

用两个钉子把一根木条钉在木板上，就能固定木条，这说明________________．

12．绝对值不大于3的非负整数有________________．

13．已知一个角的补角比这个角的余角的3倍大10°，则这个角的度数是________．

14．【母题：教材P134练习T1】自习课上，一名同学抬头看见挂在黑板上方的时钟显示为8：30，此时时针与分针的夹角是________．

15．已知点O在直线AB上，且线段OA＝4 cm，线段OB＝6 cm，点E，F分别是OA，OB的中点，则线段EF的长为________cm.

16．【母题：教材P123习题T10】如图是一个正方体的展开图，已知正方体中相对的面上的数或代数式互为相反数，则3x＋2y的值为________．

17．已知x2＋xy＝2，y2＋xy＝3，则2x2＋5xy＋3y2＝________．

18．【2022·绥化】在长为2，宽为x(1＜x＜2)的长方形纸片上，从它的一侧剪去一个以长方形纸片宽为边长的正方形(第一次操作)；从剩下的长方形纸片一侧再剪去一个以宽为边长的正方形(第二次操作)；按此方式，如果第三次操作后，剩下的纸片恰为正方形，则x的值为______________．

三、解答题(19，20题每题6分，24，25题每题12分，其余每题10分，共66分)

19．【母题：教材P51复习题T5】计算：

(1)－10－|－8|÷(－2)×；　　　　　(2)－3×23－(－3×2)3＋48÷.

20.【母题：教材P111复习题T2】解方程：

(1)8x＝－2(x＋4);     (2)－1＝.

21．先化简，再求值：

已知|2a＋1|＋(4b－2)2＝0，求3ab2－＋6a2b的值．

22．如图，点C，D是线段AB上的两点，M，N分别是AC与BD的中点．

(1)若AB＝24，CD＝18，求MN的长；

(2)若AB＝a，CD＝b，请用含a，b的式子表示MN的长．

23．【2022·娄底】“绿水青山就是金山银山”，科学研究表明：树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物，具有滞尘净化空气的作用．已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少

4 mg，若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为62 mg.

(1)请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量；

(2)娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树，据估计三棵银杏树共有约50 000片树叶．问这三棵银杏树一年的平均滞尘总量约多少千克？

24．【问题背景】落实“双减”政策后，某校开展了丰富多彩的科技活动．如图①，电子蚂蚁P，Q在长18分米的赛道AB上同时相向匀速运动，电子蚂蚁P从A出发，速度为4分米/分，电子蚂蚁Q从B出发，速度为2分米/分，当电子蚂蚁P到达B时，电子蚂蚁P，Q停止运动，经过几分P，Q之间相距6分米？

【问题解决】小辰同学在学习《有理数》之后，发现运用数形结合的方法建立数轴可以较快地解决上述问题：如图②，将点A与数轴的原点O重合，单位长度为1分米，点B落在正半轴上．设运动的时间为t(0≤t≤4.5)分钟．

(1)t分钟后点P在数轴上对应的数是________；点Q对应的数是________；(用含t的代数式表示)

(2)我们知道，如果数轴上M，N两点分别对应数m，n，则MN＝|m－n|.试运用该方法求经过几分钟P，Q之间相距6分米．

(3)在赛道AB上有一个标记位置C，AC＝6，若电子蚂蚁P与标记位置C之间的距离为a，电子蚂蚁Q与B之间的距离为b，在运动过程中，是否存在某一时刻，使得a＋b＝4？若存在，请求出运动的时间；若不存在，请说明理由．

25．如图①，点O为直线AB上一点，过点O作射线OC，将一个直角三角尺按图中所示的方式摆放(∠MON＝90°)．

(1)将图①中的三角尺绕点O在平面内旋转一定的角度得到图②，使边OM恰好平分∠BOC，问：ON是否平分∠AOC？请说明理由．

(2)将图①中的三角尺绕点O在平面内旋转一定的角度得到图③，使边ON在∠BOC的内部，如果∠BOC＝60°，则∠BOM与∠NOC之间存在怎样的数量关系？请说明理由．

答案

一、1.A　【点拨】由题意可知，图②表示的过程是在计算(－13)＋(＋23)＝10，故选A.

2．D　【点拨】－2－1＝－3，－2(x－3y)＝－2x＋6y，3÷6×＝3××＝，5x2－2x2＝3x2，故选D.

3．B　

4．A　【点拨】3A－2B＝3(x2－xy)－2(xy＋y2)＝3x2－3xy－2xy－2y2＝3x2－2y2－5xy，故选A.

5．B　点拨：将x＝－7代入方程，得2×(－7)－7＝a×(－7)，解得a＝3，则a－＝3－1＝2，故选B.

6．B　【点拨】该几何体从正面看到的图形如图所示，故选B.

7．A　【点拨】将方程整理后得(m2－1)x2－(m＋1)x＋2＝0.

因为方程为关于x的一元一次方程，

所以m2－1＝0且－(m＋1)≠0，

所以m＝1.

所以|m－1|＝0.

8．C　【点拨】AB＝AC＋BC＝3BC，即BC＝AB，故选C.

9．B　【点拨】由线段中点的定义可知说法①正确；如图①，AC＝BC，但点C不是AB的中点，则说法②错误；

由角平分线的定义可知说法③正确；如图②，∠AOC＝∠AOB，但OC不是∠AOB的平分线，则说法④错误．

故正确的说法有2个，故选B.

10．B　【点拨】设第一天走了x里，则第二天走了里，第三天走了里，第四天走了里，第五天走了里，第六天走了里，可列方程x＋＋＋＋＋＝378，解得x＝192，则第三天走的路程为＝48(里)，故选B.

二、11.经过一点可以画无数条直线；两点确定一条直线

12．0，1，2，3　【点拨】绝对值不大于3的非负整数有0，1，2，3.

13．50°　【点拨】设这个角的度数是x°，则它的余角是(90－x)°，它的补角是(180－x)°.根据题意得180－x＝3(90－x)＋10，解得x＝50.所以这个角的度数是50°.

14．75°　【点拨】如图，时针与分针的夹角为×2＋×＝75°.

15．1或5　【点拨】如图①，EF＝＝5(cm)，

如图②，EF＝＝1(cm)，则线段EF的长为1或5 cm.

16．－1　【点拨】由题意可知2x－3＝－5，y＝－x，解得x＝－1，y＝1，则3x＋2y＝－1.

17．13　【点拨】2x2＋5xy＋3y2＝2(x2＋xy)＋3(xy＋y2)＝2×2＋3×3＝13.

18．1.2或1.5　【点拨】如图①，根据题意可列方程＋2－x＝x，解得x＝1.2；

如图②，根据题意可列方程3(2－x)＝x，解得x＝1.5.

故x的值为1.2或1.5.

三、19.【解】(1)原式＝－10－8××(－)

＝－10－2

＝－12.

(2)原式＝－3×8－(－6)3＋48×(－4)

＝－24＋216－192

＝0.

20．【解】(1)去括号，得8x＝－2x－8，

移项、合并同类项，得10x＝－8，

系数化为1，得x＝－0.8.

(2)去分母，得3(3x－1)－12＝2(5x－7)，

去括号，得9x－3－12＝10x－14，

移项，得9x－10x＝－14＋3＋12，

合并同类项，得－x＝1，

系数化为1，得x＝－1.

21．【解】因为|2a＋1|＋(4b－2)2＝0，

所以2a＋1＝0，4b－2＝0，

所以a＝－，b＝.

3ab2－[5a2b＋2＋ab2]＋6a2b

＝3ab2－(5a2b＋2ab2－1＋ab2)＋6a2b

＝3ab2－(5a2b＋3ab2－1)＋6a2b

＝3ab2－5a2b－3ab2＋1＋6a2b

＝a2b＋1.

将a＝－，b＝代入，

得原式＝a2b＋1＝×＋1＝.

22．【解】(1)因为AB＝AC＋CD＋BD＝24，CD＝18，

所以AC＋BD＝24－18＝6.

因为M，N分别是AC与BD的中点，

所以CM＝AC，DN＝BD，

所以CM＋DN＝AC＋BD＝(AC＋BD)＝×6＝3，

所以MN＝MC＋DC＋DN＝3＋18＝21.

(2)由(1)知AC＋BD＝a－b，

CM＋DN＝AC＋BD＝(a－b)．

所以MN＝CM＋DN＋DC＝(a－b)＋b＝a＋b＝(a＋b)．

23．【解】(1)设一片银杏树叶一年的平均滞尘量为x mg，则一片国槐树叶一年的平均滞尘量为(62－x)mg，

由题意得x＝2(62－x)－4.

解得x＝40.

62－x＝22.

答：一片银杏树叶一年的平均滞尘量为40 mg，一片国槐树叶一年的平均滞尘量为22 mg；

(2)50 000×40＝2 000 000(mg)＝2 kg.

答：这三棵银杏树一年的平均滞尘总量约2 kg.

24．【解】(1)4t；18－2t

(2)由题意得|4t－(18－2t)|＝6，

所以|4t－18＋2t|＝6，

所以6t－18＝6或6t－18＝－6，

所以t＝4或t＝2，

所以经过2分钟或4分钟，P、Q之间相距6分米．

(3)因为AC＝6，

所以点C表示的数为6，

因为电子蚂蚁P与标记位置C之间的距离为a，电子蚂蚁Q与B之间的距离为b，

所以a＝|4t－6|，b＝|18－ (18－2t)|＝2t，

因为a＋b＝4，

所以|4t－6|＋2t＝4，

所以|4t－6|＝4－2t，

所以4t－6＝4－2t或4－6t＝2t－4，

所以t＝或t＝1，

所以存在t＝或t＝1，使得a＋b＝4.

【点拨】1.求数轴上的点表示的数时，转化为求该点到原点之间的线段的长度，然后利用该点在原点的左侧还是右侧确定数．

2．若数轴上有A，B 两点，A点表示的数为a，B 点表示的数为b，O为原点，则OA＝|a|，OB＝|b|，AB＝|a－b|.

25．【解】(1)ON平分∠AOC.

理由如下：

因为∠MON＝90°，

所以∠BOM＋∠AON＝90°，∠MOC＋∠NOC＝90°.

又因为OM平分∠BOC，

所以∠BOM＝∠MOC，

所以∠AON＝∠NOC，

所以ON平分∠AOC.

(2)∠BOM＝∠NOC＋30°.

理由如下：

因为∠NOC＋∠NOB＝60°，∠BOM＋∠NOB＝90°，

所以∠BOM＝90°－∠NOB＝90°－(60°－∠NOC)＝∠NOC＋30°.