人教版八年级数学上册单元检测 第十三章

第十三章

一、选择题(每题3分，共30分)

1．【2022·武汉】现实世界中，对称现象无处不在，中国的方块字有些也具有对称性，下列汉字是轴对称图形的是(　　)

2．【2023·兰州东方中学模拟】在平面直角坐标系xOy中，点A(－3，4)关于y轴对称的点B的坐标是(　　)

A．(3，－4)  B．(－3，－4)  C．(－3，4)  D．(3，4)

3．如图，在△ABC中，已知AB＝AC，点D在CA的延长线上，∠DAB＝50°，则∠B的度数为(　　)

A．25°  B．30°  C．40°  D．45°

4．【2022·百色】如图，是求作线段AB中点的作图痕迹，则下列结论不一定成立的是(　　)

A．∠B＝45°  B．AE＝EB  C．AC＝BC  D．AB⊥CD

5．如图，直线a∥b，等边三角形ABC的顶点C在直线b上，∠2＝40°，则∠1的度数为(　　)

A．80°  B．70°  C．60°  D．50°

6．如图，在等腰三角形ABC中，BA＝BC，∠ABC＝120°，D为AC边的中点．若BC＝6，则BD的长为(　　)

A．3  B．4  C．6  D．8

7．如图，在平面直角坐标系中，有点A(－2，4)和点B(4，2)，在x轴上取一点P，使点P到点A和点B的距离之和最小，则点P的坐标是(　　)

A．(－2，0)  B．(4，0)  C．(2，0)  D．(0，0)

8．【母题：教材P66习题T12】某地兴建的幸福小区的三个出口A、B、C的位置如图所示，物业公司计划在不妨碍小区规划的建设下，想在小区内修建一个电动车充电桩，以方便业主，要求到三个出口的距离都相等，则充电桩应该修建在△ABC(　　)

A．三条高线的交点处  　　　　    　B．三条中线的交点处

C．三个角的平分线的交点处  　　  　D．三条边的垂直平分线的交点处

9．在平面直角坐标系xOy中，已知点A(2，－2)，在y轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P有(　　)

A．1个  B．2个  C．3个  D．4个

10．如图，在四边形ABCD中，∠C＝50°，∠B＝∠D＝90°，E，F分别是BC，DC上的点，当△AEF的周长最小时，∠EAF的度数为(　　)

A．50°  B．60°  C．70°  D．80°

二、填空题(每题3分，共24分)

11．若点M(3，a－2)，N(b，a)关于x轴对称，则a＋b＝________.

12．【2022·苏州】定义：一个三角形的一边长是另一边长的2倍，这样的三角形叫做“倍长三角形”．若等腰三角形ABC是“倍长三角形”，底边BC的长为3，则腰AB的长为________．

13．如图，在三角形纸片ABC中，AB＝8 cm，BC＝5 cm，AC＝6 cm，沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，则△AED的周长等于________cm.

14．【2023·黄冈启黄中学模拟】如图，在Rt△ABC中，∠C＝90°，∠B＝30°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点E，F；再分别以点E，F为圆心，大于EF的长为半径画弧，两弧交于点P，作射线AP交BC于点D，则CD与BD的数量关系是________．

15．小明上午在理发店时，从镜子内看到背后普通时钟的时针与分针的位置如图所示，此时的时间是__________．

16．如图，在△ABC中，AF平分∠BAC，AC的垂直平分线DE交BC于点E，交AC于点D，∠B＝70°，∠FAE＝19°，则∠C＝________°.

17．【母题：教材P83习题T10】如图，∠ABC，∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于点D，交AC于点E，有下列结论：①△BDF，△CEF都是等腰三角形；②DE＝BD＋CE；③△ADE的周长为AB＋AC；④BD＝CE.其中正确的有__________(填序号)．

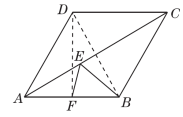
18．如图，在四边形ABCD中，AB＝BC＝CD＝AD，点D到AB的距离为3，∠BAD＝60°，点F为AB的中点，点E为AC上的任意一点，则EF＋EB的最小值为________．

三、解答题(19～21题每题10分，22～24题每题12分，共66分)

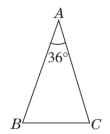
19．如图，已知等腰三角形ABC的顶角∠A＝36°.

(1)在AC上作一点D，使AD＝BD(要求：尺规作图，保留作图痕迹，不必写作法和证明)；

(2)求证：△BCD是等腰三角形．

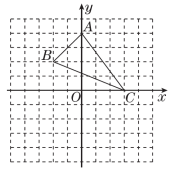
20．如图，已知A(0，4)，B(－2，2)，C(3，0)．

(1)作△ABC关于x轴对称的△A1B1C1；

(2)写出点A1，B1，C1的坐标；

(3)△A1B1C1的面积为________．

21．为了进一步改善人居环境，提高居民生活的幸福指数，某小区物业公司决定对小区环境进行优化改造．如图，AB表示该小区一段长为20 m的斜坡，坡角∠BAD＝30°，BD⊥AD于点D，为方便通行，在不改变斜坡高度的情况下，把坡角降为15°.

(1)求该斜坡的高度BD；

(2)求斜坡新起点C与原起点A之间的距离．(假设图中C，A，D三点共线)

22．在△ABC中，AC＜AB＜BC.

(1)如图①，已知线段AB的垂直平分线与BC边交于点P，连接AP，求证：

∠APC＝2∠B；

(2)如图②，以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连接AQ.若∠AQC＝3∠B，求∠B的度数．

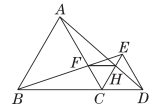
23．【母题：教材P83习题T12】如图，已知点B，C，D在同一条直线上，△ABC和△CDE都是等边三角形，BE交AC于点F，AD交CE于点H.

(1)求证：△BCE≌△ACD；

(2)求证：CF＝CH；

(3)判断△CFH的形状并说明理由．

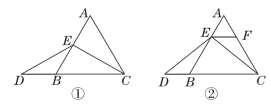
24．【母题：教材P93复习题T13】在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且AE＝BD.试探索以下问题：

(1)当点E为AB的中点时，如图①，求证：EC＝ED；

(2)如图②，当点E不是AB的中点时，过点E作EF∥BC，交AC于点F，求证：△AEF是等边三角形；

(3)在(2)的条件下，EC与ED还相等吗？请说明理由．

答案

一、1.D　2.D　3.A　4.A　5.A　6.A

7．C　【点拨】作A关于x轴的对称点C，连接BC交x轴于P，连接AP.则此时AP＋PB最小，即此时点P到点A和点B的距离之和最小．

8．D

9．D　　【点拨】当OA为等腰三角形的腰时，以O为圆心，OA为半径画弧，与y轴有两个交点；以A为圆心，OA为半径画弧，与y轴除点O外还有一个交点；当OA为等腰三角形的底边时，作线段OA的垂直平分线，与y轴有一个交点．所以符合条件的点一共有4个．

10．D　【点拨】如图，分别作点A关于直线BC和CD的对称点A′，A″，连接A′A″，交BC于点E，交CD于点F，连接AE，AF，则A′A″的长即为△AEF的周长的最小值．作DA的延长线AH.

∵∠C＝50°，∠ABC＝∠ADC＝90°，

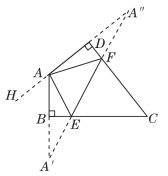
∴∠DAB＝130°.

∴∠HAA′＝50°.

∴∠AA′E＋∠A″＝∠HAA′＝50°.

易知∠EA′A＝∠EAA′，∠A″AF＝∠A″，

∴∠EAA′＋∠A″AF＝50°.

∴∠EAF＝130°－50°＝80°.

二、11.4　12.6　13.9

14．CD＝BD　【点拨】先根据直角三角形的性质可得∠BAC＝60°，再根据角平分线的尺规作图可知AD平分∠BAC，从而可得∠CAD＝∠BAD＝30°，然后根据等腰三角形的判定方法可得AD＝BD，最后根据直角三角形的性质可得CD＝AD，由此即可得出答案．

15．10：45　【点拨】镜子中的时间和实际时间关于钟表上过6和12的直线对称，作出相应图形，即可得到准确时间．

16．24

17．①②③　【点拨】∵DE∥BC，

∴∠DFB＝∠FBC, ∠EFC＝∠FCB.

∵BF是∠ABC的平分线，CF是∠ACB的平分线，

∴∠FBC＝∠DBF，∠FCE＝∠FCB，

∴∠DBF＝∠DFB，∠EFC＝∠ECF，

∴DF＝DB，FE＝EC，即有DE＝DF＋FE＝DB＋EC，

∴△ADE的周长＝AD＋AE＋DE＝AD＋AE＋DB＋EC＝AB＋AC.

18．3　【点拨】如图，连接BD.∵AB＝BC＝CD＝AD，∴AC垂直平分BD.∴点B关于直线AC的对称点为点D.连接DF，则DF的长即为EF＋EB的最小值．在△ABD中，由∠BAD＝60°，AD＝AB，可得△ABD为等边三角形．∵点F为AB的中点，∴DF⊥AB.∴DF＝3.∴EF＋EB的最小值为3.

三、19.(1)【解】如图所示．

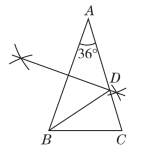
(2)【证明】∵AB＝AC，∠A＝36°，

∴∠C＝(180°－∠A)＝(180°－36°)＝72°.

∵AD＝BD，∴∠A＝∠ABD.

∴∠BDC＝∠A＋∠ABD＝2∠A＝2×36°＝72°.

∴∠BDC＝∠C.

∴BD＝BC.∴△BCD是等腰三角形．

20．【解】(1)如图所示．

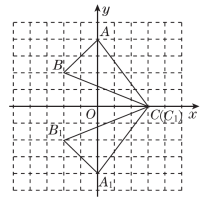
(2)A1(0，－4)，B1(－2，－2)，C1(3，0)．

(3)7

21．【解】(1)∵∠BAD＝30°，BD⊥AD，AB＝20 m，

∴BD＝AB＝10 m.

(2)∵C，A，D三点共线，∠BAD＝30°，∠ACB＝15°，

∴∠ABC＝∠BAD－∠C＝15°，

∴AC＝AB＝20 m.

22．(1)【证明】∵点P在线段AB的垂直平分线上，

∴PA＝PB.∴∠PAB＝∠B.

∵∠APC＝∠PAB＋∠B，∴∠APC＝2∠B.

(2)【解】根据题意，得BQ＝BA，

∴∠BAQ＝∠BQA.

设∠B＝x，则∠AQC＝∠B＋∠BAQ＝3x，

∴∠BAQ＝∠BQA＝2x.

在△ABQ中，x＋2x＋2x＝180°，

解得x＝36°.∴∠B＝36°.

23．(1)【证明】∵△ABC和△CDE都是等边三角形，

∴BC＝AC，CE＝CD，∠ACB＝∠ECD＝60°.

∴∠BCE＝60°＋∠ACE＝∠ACD.

∴△BCE≌△ACD(SAS)．

(2)【证明】∵△BCE≌△ACD，

∴∠FBC＝∠HAC.

∵∠ACB＝∠ECD＝60°，

∴∠FCH＝180°－∠ACB－∠ECD＝60°，

∴∠BCF＝∠ACH.

又∵BC＝AC，

∴△BCF≌△ACH(ASA)．

∴CF＝CH.

(3)【解】△CFH是等边三角形．

理由：∵CF＝CH，∠FCH＝60°，

∴△CFH是等边三角形．

24．(1)【证明】∵△ABC是等边三角形，

∴∠ABC＝∠ACB＝∠A＝60°.

∵E是AB的中点，

∴AE＝EB，∠ECB＝∠ACB＝×60°＝30°.

∵AE＝BD，∴BE＝BD.

∴∠EDB＝∠DEB＝∠ABC＝×60°＝30°.

∴∠EDB＝∠ECB.∴EC＝ED.

(2)【证明】∵EF∥BC，

∴∠AEF＝∠ABC＝60°，∠AFE＝∠ACB＝60°.

又∵∠A＝60°，∴△AEF是等边三角形．

(3)【解】ED＝EC.理由如下：

由(2)得△AEF是等边三角形，

∴AE＝EF＝AF.

∵AE＝BD，AB＝AC，∴BD＝EF，BE＝FC.

又∵∠AFE＝∠ABC＝60°，

∴∠EFC＝∠DBE＝120°.

∴△DBE≌△EFC(SAS)．∴ED＝EC.