人教版八年级数学上册 期末检测卷

这是一份人教版八年级数学上册 期末检测卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
期末综合一、选择题(每题3分，共30分)1．【2022·乐山】如下字体的四个汉字中，是轴对称图形的是(　　)2．【母题：教材P128例1】使分式有意义的x的取值范围是(　　)A．x≥  B．x≤  C．x＞  D．x≠3．如图，△OAD≌△OBC，且∠O＝70°，∠C＝25°，则∠OAD＝(　　)A．95°  B．85°  C．75°  D．65°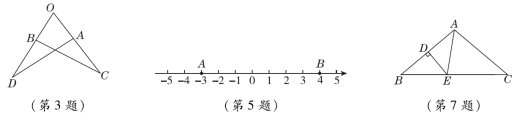4．【母题：教材P112习题T7】已知a＋b＝12，a－b＝10，则a2－b2的值是(　　)A．22  B．30  C．60  D．1205．【2022·西藏】如图，数轴上A，B两点到原点的距离是三角形两边的长，则该三角形第三边长可能是(　　)A．－5  B．4  C．7  D．86．已知2m＋3n＝5，则4m·8n＝(　　)A．16  B．25  C．32  D．647．如图，在△ABC中，AB＝AC，∠BAC＝100°，AB的垂直平分线DE分别交AB，BC于点D，E，则∠BAE＝(　　)A．80°  B．60°  C．50°  D．40°8．【2022·云南】某地开展建设绿色家园活动，活动期间，计划每天种植相同数量的树木．该活动开始后，实际每天比原计划每天多植树50棵，实际植树400棵所需时间与原计划植树300棵所需时间相同．设实际每天植树x棵，则下列方程正确的是(　　)A.＝  B.＝  C.＝  D.＝9．如图，在△ABC中，∠BAC＝108°，将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上，且AB′＝CB′，则∠C′的度数为(　　)A．18°  B．20°  C．24°  D．28°10．如图，过边长为1的等边三角形ABC的边AB上一点P，作PE⊥AC于点E，Q为BC延长线上一点，当AP＝CQ时，PQ交AC于点D，则DE的长为(　　)A.  B.  C.  D．不能确定二、填空题(每题3分，共24分)11．2023年3月举行的“第十三届中国国际纳米技术产业博览会”，纳米技术也称毫微技术，是研究结构尺寸在1纳米至100纳米范围内材料的性质和应用的一种技术.1纳米等于0.000 000 001米，9纳米可用科学记数法表示为________米．12．【母题：教材P118例6】分解因式：ax2－2ax＋a＝____________．13．【2023·山东实验中学模拟】在平面直角坐标系中，点A(3，2)关于x轴的对称点为A1，将点A1向左平移3个单位长度得到点A2，则A2的坐标为__________．14．如图，AB＝AC，AD＝AE，∠BAC＝∠DAE，点D在线段BE上．若∠1＝25°，∠2＝30°，则∠3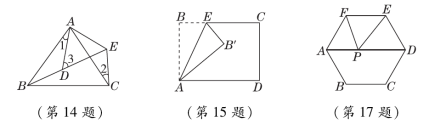＝______．15．将长方形ABCD沿AE折叠，得到如图的图形．已知∠CEB′＝50°，则∠B′AD的度数为________．16．【2023·郑州中原区月考】若关于x的分式方程－1＝无解，则m＝__________．17．如图，已知正六边形ABCDEF的边长是5，点P是AD上的一个动点，则PE＋PF的最小值是________．18．如图，在平面直角坐标系中，点A，B分别在y轴和x轴上，∠ABO＝60°，在坐标轴上找一点P，使得△PAB是等腰三角形，则符合条件的P点共有________个．三、解答题(19，20，21题每题8分， 22，23，24题每题10分，25题12分，共66分)19．计算：(1)x(x－2y)－(x＋y)2；　　　　　　(2)÷.    20．【母题：教材P158复习题T4】解方程：(1)＝＋1；　　　　　　　　　　(2)＝－.      21．(1)先化简，再求值：(2＋a)(2－a)＋a(a－2b)＋3a5b÷(－a2b)4，其中ab＝－.    (2)因式分解：a(n－1)2－2a(n－1)＋a.      22．【母题：教材P72习题T7】如图，已知网格上最小的正方形的边长为1.(1)分别写出A，B，C三点的坐标．(2)作△ABC关于y轴对称的△A′B′C′(不写作法)，想一想：关于y轴对称的两个点之间有什么关系？(3)求△ABC的面积．   23．如图，已知AB＝AC，AD＝AE，BD和CE相交于点O.(1)求证：△ABD≌△ACE；(2)判断△BOC的形状，并说明理由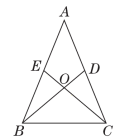．  24．为了迎接在杭州举行的第19届亚运会，某旅游商店购进若干吉祥物钥匙扣和明信片，已知吉祥物钥匙扣的进价为18元/个，明信片的进价为6元/套，一个吉祥物钥匙扣的售价比一套明信片的售价高20元，若顾客花150元购买的吉祥物钥匙扣数量与花50元购买的明信片数量相同．(1)求吉祥物钥匙扣和明信片的售价；(2)为了促销，商店对吉祥物钥匙扣进行9折销售，某顾客同时购买吉祥物钥匙扣和明信片两种商品若干件，商家获毛利80元，请问有几种购买方案？     25．如图①，在四边形ABCD中，已知∠ABC＋∠ADC＝180°，AB＝AD，DA⊥AB，点E在CD的延长线上，∠BAC＝∠DAE.　(1)求证：△ABC≌△ADE；(2)求证：CA平分∠BCD；(3)如图②，若AF是△ABC的边BC上的高，求证：CE＝2AF. 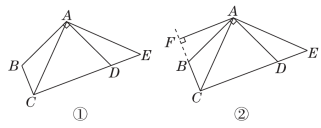答案一、1.D　2.D　3.B　4.D　5.B　6.C　7.D　8.B　9.C10．B　【点拨】过点P作PF∥BC交AC于点F.由△ABC为等边三角形，易得△APF也是等边三角形，∴AP＝PF.∵AP＝CQ，∴PF＝CQ.又∵PF∥CQ，∴∠DPF＝∠DQC，∠DFP＝∠DCQ.∴△PFD≌△QCD(ASA)．∴DF＝DC.∵PE⊥AF，且PF＝PA，∴AE＝EF.∴DE＝DF＋EF＝CF＋AF＝AC＝×1＝.二、11.9×10－9　12.a(x－1)2　13.(0，－2)14．55°　15.40°　16.2　17．10　【点拨】利用正多边形的性质可得点F关于直线AD的对称点为点B，连接BE交AD于点P′，连接FP′，则P′B＝P′F.∴P′E＋P′F＝P′E＋P′B＝BE.当点P与点P′重合时，PE＋PF的值最小，最小值为BE的长．易知△AP′B和△EP′F均为等边三角形，∴P′B＝P′E＝5，∴BE＝10，∴PE＋PF的最小值是10.18．6　【点拨】如图．①当AB＝AP时，在y轴上有2个满足条件的点P，在x轴上有1个满足条件的点P.  ②当AB＝BP时，在y轴上有1个满足条件的点P，在x轴上有2个满足条件的点P，有1个点与AB＝AP时在x轴正半轴的点P重合．③当AP＝BP时，在x轴，y轴上各有1个满足条件的点P，有1个与AB＝AP时的x轴正半轴的点P重合．综上所述，符合条件的点P共有6个．三、19.【解】(1)原式＝x2－2xy－x2－2xy－y2＝－4xy－y2；(2)原式＝·＝·＝.20．【解】(1)方程两边乘x2－1，得x(x＋1)＝3(x－1)＋x2－1，解得x＝2.检验：当x＝2时，x2－1≠0，∴原分式方程的解为x＝2.(2)去分母，得2(x＋1)＝6(2x－1)－4(2x＋1)．去括号，得2x＋2＝12x－6－8x－4，解得x＝6.经检验，x＝6是分式方程的解．∴原分式方程的解为x＝6.21．【解】(1)原式＝4－a2＋a2－2ab＋3a5b÷a8b4＝4－2ab＋3a－3b－3.当ab＝－时，原式＝4－2×＋3×＝4＋1－＝5－24＝－19.(2)原式＝a[(n－1)2－2(n－1)＋1]＝a(n－1－1)2＝a(n－2)2.22．【解】(1)A(－3，3)，B(－5，1)，C(－1，0)．(2)图略．关于y轴对称的两个点的横坐标互为相反数，纵坐标相等，两点连线被y轴垂直平分．(3)S△ABC＝3×4－×2×3－×2×2－×4×1＝5.23．(1)【证明】在△ABD和△ACE中，∴△ABD≌△ACE(SAS)．(2)【解】△BOC是等腰三角形．理由：∵△ABD≌△ACE，∴∠ABD＝∠ACE.∵AB＝AC，∴∠ABC＝∠ACB.∴∠ABC－∠ABD＝∠ACB－∠ACE，即∠OBC＝∠OCB.∴BO＝CO，即△BOC是等腰三角形．24．【解】(1)设吉祥物钥匙扣的售价为x元，则明信片的售价为(x－20)元，由题意，得＝，解得x＝30，经检验，x＝30是原方程的解，且符合题意，则x－20＝10.答：吉祥物钥匙扣的售价为30元，明信片的售价为10元．(2)设购买吉祥物钥匙扣m个，明信片n套，由题意，得(30×0.9－18)m＋(10－6)n＝80，整理，得n＝20－m，∵m、n为正整数，∴或∴有2种购买方案．答：有2种购买方案．25．【证明】(1)∵∠ABC＋∠ADC＝180°，∠ADE＋∠ADC＝180°，∴∠ABC＝∠ADE.在△ABC和△ADE中，∴△ABC≌△ADE(ASA)．(2)∵△ABC≌△ADE，∴AC＝AE，∠BCA＝∠E.∴∠ACD＝∠E.∴∠BCA＝∠ACD，即CA平分∠BCD.(3)如图，过点A作AM⊥CE，垂足为点M.  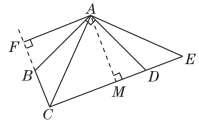∵AM⊥CD，AF⊥CF，∠BCA＝∠ACD，∴AF＝AM.∵∠BAC＝∠DAE，∴∠CAE＝∠CAD＋∠DAE＝∠CAD＋∠BAC＝∠BAD＝90°.∴∠ACE＝∠E＝45°.∵AM⊥CE，∴∠ACE＝∠CAM＝∠EAM＝∠E＝45°.∴CM＝AM＝ME.又∵AF＝AM，∴CE＝CM＋ME＝2AM＝2AF.