高考数学一轮复习夯基练习：不等式的性质与一元二次不等式(含答案)

这是一份高考数学一轮复习夯基练习：不等式的性质与一元二次不等式(含答案)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
夯基练习 不等式的性质与一元二次不等式一 、选择题1.若A=(x＋3)(x＋7)，B=(x＋4)(x＋6)，则A，B的大小关系为(　　)A．A<B         B．A=B          C．A>B         D．不确定  2.不等式|x-5|＋|x＋3|≥10的解集是(　　)A．[-5,7]                         B．[-4,6]C. (-∞，-5]∪[7，＋∞)           D. (-∞，-4]∪[6，＋∞)  3.设集合A={(x，y)|x－y≥1，ax＋y>4，x－ay≤2}，则(　　)A．对任意实数a，(2,1)∈A         B．对任意实数a，(2,1)∉AC．当且仅当a<0时，(2,1)∉A       D．当且仅当a≤时，(2,1)∉A   4.不等式2x2-x-3＞0的解集是(　　)A．(-1.5，1)               B．(-∞，-1)∪(1.5，＋∞) C．(-1，1.5)               D．(-∞，-1.5)∪(1，＋∞)  5.若0<t<1，则不等式(x-t)(x-)<0的解集为(　　)A.{x|<x<t}　      B.{x|x>或x<t}    C.{x|x<或x>t}      D.{x|t<x<}6.设a，b∈[0，＋∞)，A=＋，B=，则A，B的大小关系是(　　)A．A≤B           B．A≥B        C．A<B            D．A>B  7.设m＋n＞0，则关于x的不等式(m－x)(n＋x)＞0的解是(　　)A.x＜－n或x＞m         B.－n＜x＜mC.x＜－m或x＞n         D.－m＜x＜n  8.已知a∈Z，关于x的一元二次不等式x2－6x＋a≤0的解集中有且仅有3个整数，则所有符合条件的a的值之和是(　　)A．13            B．18            C．21            D．26  9.已知函数f(x)=-x2+ax+b2-b+1(a∈R,b∈R),对任意实数x都有f(1-x)=f(1+x)成立,当x∈[-1,1]时, f(x)>0恒成立,则b的取值范围是(　　)A.-1<b<0                                                      B.b>2           C.b<-1或b>2                                       D.不能确定10.若不等式-3≤x2-2ax＋a≤-2有唯一解，则a的值是(　　)A．2或-1          B．          C．          D．2  11.若关于x的不等式x2＋2ax＋1≥0在[0，＋∞)上恒成立，则实数a的取值范围为(　　)A．(0，＋∞)       B．[－1，＋∞)        C．[－1，1]         D．[0，＋∞)  12.设函数g(x)=x2－2(x∈R)，f(x)=则f(x)的值域是(　　)A.[-2.25,0]∪(1，＋∞)        B.[0，＋∞)C.[-2.25,+∞)                 D.[-2.25,0]∪(2，＋∞)   二 、填空题13.设|x-2|＜a时，不等式|x2-4|＜1成立，则正数a的取值范围为____________．  14.已知函数f(x)=x2＋mx-1，若对于任意x∈[m，m＋1]，都有f(x)<0，则实数m的取值范围是________．  15.不等式x2＋ax＋4＜0的解集不是空集，则实数a的取值范围是________．  16.已知不等式|x2-4x＋a|＋|x-3|≤5的x的最大值为3，则实数a的值是____________．   三 、解答题17. (1)已知x≤1，比较3x3与3x2－x＋1的大小；(2)若－1＜a＜b＜0，试比较，，a2，b2的大小．            18.已知f(x)=-3x2＋a(6-a)x＋6.(1)解关于a的不等式f(1)＞0；(2)若不等式f(x)＞b的解集为(-1,3)，求实数a，b的值．                19.已知函数f(x)=的定义域为R.(1)求a的取值范围；(2)若函数f(x)的最小值为，解关于x的不等式x2－x－a2－a＜0.                20.已知函数y=(k2＋4k－5)x2＋4(1－k)x＋3的图像都在x轴的上方，求实数k的取值范围. 
参考答案1.答案为：A；解析：因为(x＋3)(x＋7)－(x＋4)(x＋6)=(x2＋10x＋21)－(x2＋10x＋24)=－3<0，故A<B．  2.答案为：D；解析：当x≤-3时，|x-5|＋|x＋3|=5-x-x-3=2-2x≥10，即x≤-4，∴x≤-4.当-3＜x＜5时，|x-5|＋|x＋3|=5-x＋x＋3=8≥10，不成立，∴无解．当x≥5时，|x-5|＋|x＋3|=x-5＋x＋3=2x-2≥10，即x≥6，∴x≥6.综上可知，不等式的解集为(-∞，-4]∪[6，＋∞)．  3.答案为：D；解析：若(2,1)∈A，则有解得a>．结合四个选项，只有D说法正确．故选D．  4.答案为： B；解析：2x2-x-3＞0可因式分解为(x＋1)(2x-3)＞0，解得x＞1.5或x＜-1，∴不等式2x2-x-3＞0的解集是(-∞，-1)∪(1.5，＋∞)．故选B．  5.答案为：D；6.答案为：B；解析：由题意，得B2－A2=－2≤0，且A≥0，B≥0，可得A≥B．故选B．  7.答案为：B；解析：方程(m－x)(n＋x)=0的两根为m，－n，因为m＋n＞0，所以m＞－n，结合函数y=(m－x)(n＋x)的图象，得原不等式的解是－n＜x＜m，故选B.  8.答案为：C.设f(x)=x2－6x＋a，其图象是开口向上，对称轴是x=3的抛物线，如图所示．解析：关于x的一元二次不等式x2－6x＋a≤0的解集中有且仅有3个整数，则，即，解得5＜a≤8，又a∈Z，所以a=6，7，8，所有符合条件的a的值之和是6＋7＋8=21.选C.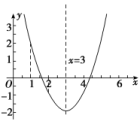  9.答案为：C；解析：由f(1-x)=f(1+x)知, f(x)图象的对称轴为直线x=1,则有=1,故a=2.由f(x)的图象可知f(x)在[-1,1]上为增函数,∴x∈[-1,1]时, f(x)min=f(-1)=-1-2+b2-b+1=b2-b-2,令b2-b-2>0,解得b<-1或b>2. 10.答案为：A；解析：令f(x)=x2-2ax＋a，即f(x)=(x-a)2＋a-a2，因为-3≤x2-2ax＋a≤-2有唯一解，所以a-a2=-2，即a2-a-2=0，解得a=2或a=-1．故选A．  11.答案为：B.解析：设f(x)=x2＋2ax＋1，函数图象的对称轴为直线x=－a，当－a≤0，即a≥0时，f(0)=1＞0，所以当x∈[0，＋∞)时，f(x)≥0恒成立；当－a＞0，即a＜0时，要使f(x)≥0在[0，＋∞)上恒成立，需f(－a)=a2－2a2＋1=－a2＋1≥0，得－1≤a＜0.综上，实数a的取值范围为[－1，＋∞)．  12.答案为：D；解析：由x＜g(x)，得x＜x2－2，则x＜－1或x＞2；由x≥g(x)，得x≥x2－2，则－1≤x≤2.因此f(x)=即f(x)=因为当x＜－1时，y＞2；当x＞2时，y＞8.所以 当x∈(－∞，－1)∪(2，＋∞)时，函数f(x)的值域为(2，＋∞).当－1≤x≤2时， －2.25≤y≤0.所以当x∈[－1，2] 时，函数f(x)的值域为[-2.25,0].综上可知，函数f(x)的值域为[-2.25,0]∪(2，＋∞).   二 、填空题13.答案为：(0，-2]；解析：由|x-2|＜a得2-a＜x＜a＋2，由|x2-4|＜1，得3＜x2＜5，所以-＜x＜-或＜x＜.因为a＞0，所以由题意得解得 0＜a≤-2，故正数a的取值范围为(0，-2]．  14.答案为：；解析：由题可得f(x)<0对于x∈[m，m＋1]恒成立，等价于解得-<m<0．  15.答案为：(-∞，-4)∪(4，＋∞)；解析：∵不等式x2＋ax＋4＜0的解集不是空集，∴Δ=a2-4×4＞0，即a2＞16.∴a＞4或a＜-4.  16.答案为：8；解析：∵x≤3，∴|x-3|=3-x.若x2-4x＋a＜0，则原不等式化为x2-3x＋a＋2≥0.此不等式的解集不可能是集合{x|x≤3}的子集，∴x2-4x＋a＜0不成立．于是，x2-4x＋a≥0，则原不等式化为x2-5x＋a-2≤0.∵x≤3，令x2-5x＋a-2=(x-3)(x-m)=x2-(m＋3)x＋3m，比较系数，得m=2，∴a=8.   三 、解答题17.解：(1)3x3－(3x2－x＋1)=(3x3－3x2)＋(x－1)=3x2(x－1)＋(x－1)=(x－1)(3x2＋1)．因为x≤1，所以x－1≤0，又3x2＋1＞0，所以(x－1)(3x2＋1)≤0，所以3x3≤3x2－x＋1.(2)因为－1＜a＜b＜0，所以－a＞－b＞0，所以a2＞b2＞0.因为a＜b＜0，所以a·＜b·＜0，即0＞＞，所以a2＞b2＞＞.  18.解：(1)∵f(x)=-3x2＋a(6-a)x＋6，∴f(1)=-3＋a(6-a)＋6=-a2＋6a＋3，∴原不等式可化为a2-6a-3＜0，解得3-2＜a＜3＋2.∴原不等式的解集为{a|3-2＜a＜3＋2}．(2)f(x)＞b的解集为(-1,3)等价于方程-3x2＋a(6-a)x＋6-b=0的两根为-1,3，等价于解得  19.解：(1)因为函数f(x)=的定义域为R，所以ax2＋2ax＋1≥0恒成立，当a=0时，1≥0恒成立．当a≠0时，则有解得0＜a≤1，综上可知，a的取值范围是[0，1]．(2)因为f(x)= = ，a＞0，所以当x=－1时，f(x)min=，由题意得，=，所以a=，所以不等式x2－x－a2－a＜0可化为x2－x－＜0.解得－＜x＜，所以不等式的解集为.  20.解：