


所属成套资源:高考数学一轮复习夯基练习 (含答案)
高考数学一轮复习夯基练习:导数在研究函数中的应用(含答案)
展开
这是一份高考数学一轮复习夯基练习:导数在研究函数中的应用(含答案),共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
夯基练习 导数在研究函数中的应用一 、选择题1.下列函数中,在(0,+∞)内为增函数的是( )A.y=sin x B.y=xex C.y=x3-x D.y=ln x-x 2.设函数f(x)在R上可导,其导函数为f′(x),且函数f(x)在x=-2处取得极小值,则函数y=xf′(x)的图象可能是( )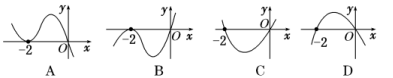 3.函数f(x)=x-ln x的单调递减区间为( )A.(0,1) B.(0,+∞) C.(1,+∞) D.(-∞,0)∪(1,+∞) 4.函数y=2x3-3x2-12x+5在[-2,1]上的最大值、最小值分别是( )A.12,-8 B.1,-8 C.12,-15 D.5,-16 5.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为( )
3.函数f(x)=x-ln x的单调递减区间为( )A.(0,1) B.(0,+∞) C.(1,+∞) D.(-∞,0)∪(1,+∞) 4.函数y=2x3-3x2-12x+5在[-2,1]上的最大值、最小值分别是( )A.12,-8 B.1,-8 C.12,-15 D.5,-16 5.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为( )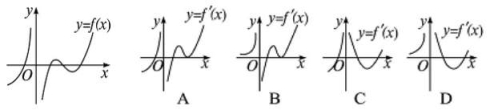 6.函数y=x4-2x2+5的单调递减区间为( )A.(-∞,-1)和(0,1) B.[-1,0]和[1,+∞)C.[-1,1] D.(-∞,-1]和[1,+∞) 7.已知函数f(x)=+ln x,则有( )A.f(2)<f(e)<f(3) B.f(e)<f(2)<f(3)C.f(3)<f(e)<f(2) D.f(e)<f(3)<f(2) 8.若函数f(x)=kx-ln x在区间(1,+∞)内单调递增,则k的取值范围是( )A.(-∞,-2] B.(-∞,-1] C.[2,+∞) D.[1,+∞) 9.已知函数f(x)=+ln x,则有( )A.f(2)<f(e)<f(3) B.f(e)<f(2)<f(3)C.f(3)<f(e)<f(2) D.f(e)<f(3)<f(2) 10.函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围为( )A.[0,1) B.(0,1) C.(-1,1) D. 11.函数
6.函数y=x4-2x2+5的单调递减区间为( )A.(-∞,-1)和(0,1) B.[-1,0]和[1,+∞)C.[-1,1] D.(-∞,-1]和[1,+∞) 7.已知函数f(x)=+ln x,则有( )A.f(2)<f(e)<f(3) B.f(e)<f(2)<f(3)C.f(3)<f(e)<f(2) D.f(e)<f(3)<f(2) 8.若函数f(x)=kx-ln x在区间(1,+∞)内单调递增,则k的取值范围是( )A.(-∞,-2] B.(-∞,-1] C.[2,+∞) D.[1,+∞) 9.已知函数f(x)=+ln x,则有( )A.f(2)<f(e)<f(3) B.f(e)<f(2)<f(3)C.f(3)<f(e)<f(2) D.f(e)<f(3)<f(2) 10.函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围为( )A.[0,1) B.(0,1) C.(-1,1) D. 11.函数![]() 的图像大致为( )
的图像大致为( ) 12.函数f(x)=x3+ax-2在区间[1,+∞)上是增函数,则实数a的取值范围是( )A.[3,+∞) B.[-3,+∞) C.(-3,+∞) D.(-∞,-3) 二 、填空题13.已知函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为____________. 14.已知函数f(x)=-2x2+ln x(a>0).若函数f(x)在[1,2]上为单调函数,则a的取值范围是________. 15.函数f(x)=cos x+x的单调递增区间是________. 16.已知函数y=f(x)=x3+3ax2+3bx+c在x=2处有极值,其图象在x=1处的切线平行于直线6x+2y+5=0,则f(x)的极大值与极小值之差为________. 三 、解答题17.已知函数f(x)=x3-3ax+b(a≠0),求函数f(x)的单调区间与极值点. 18.已知函数f(x)=x3+ax2+bx+5,曲线y=f(x)在点P(1,f(1))处的切线方程为y=3x+1.(1)求a,b的值;(2)求y=f(x)在[-3,1]上的最大值. 19.已知函数f(x)=ax3-6ax2+b在[-1,2]上有最大值3,最小值-29,求a,b的值. 20.已知f(x)=x3+ax2+bx+c在x=1与x=-2时都取得极值.(1)求a,b的值;(2)若x∈[-3,2]时都有f(x)>-恒成立,求c的取值范围.
12.函数f(x)=x3+ax-2在区间[1,+∞)上是增函数,则实数a的取值范围是( )A.[3,+∞) B.[-3,+∞) C.(-3,+∞) D.(-∞,-3) 二 、填空题13.已知函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为____________. 14.已知函数f(x)=-2x2+ln x(a>0).若函数f(x)在[1,2]上为单调函数,则a的取值范围是________. 15.函数f(x)=cos x+x的单调递增区间是________. 16.已知函数y=f(x)=x3+3ax2+3bx+c在x=2处有极值,其图象在x=1处的切线平行于直线6x+2y+5=0,则f(x)的极大值与极小值之差为________. 三 、解答题17.已知函数f(x)=x3-3ax+b(a≠0),求函数f(x)的单调区间与极值点. 18.已知函数f(x)=x3+ax2+bx+5,曲线y=f(x)在点P(1,f(1))处的切线方程为y=3x+1.(1)求a,b的值;(2)求y=f(x)在[-3,1]上的最大值. 19.已知函数f(x)=ax3-6ax2+b在[-1,2]上有最大值3,最小值-29,求a,b的值. 20.已知f(x)=x3+ax2+bx+c在x=1与x=-2时都取得极值.(1)求a,b的值;(2)若x∈[-3,2]时都有f(x)>-恒成立,求c的取值范围.
参考答案1.答案为:B;解析:B中,y′=(xex)′=ex+xex=ex(x+1)>0在(0,+∞)上恒成立,∴y=xex在(0,+∞)上为增函数.对于A、C、D都存在x>0,使y′<0的情况. 2.答案为:C;解析:由题意可得f′(-2)=0,而且当x∈(-∞,-2)时, f′(x)<0,此时xf′(x)>0;排除B、D,当x∈(-2,+∞)时,f′(x)>0,此时若x∈(-2,0),xf′(x)<0,若x∈(0,+∞),xf′(x)>0,所以函数y=xf′(x)的图象可能是C. 3.答案为:A;解析:函数的定义域是(0,+∞),且f′(x)=1-=,令f′(x)<0,解得0<x<1,所以单调递减区间是(0,1). 4.答案为:A;解析:y′=6x2-6x-12,由y′=0⇒x=-1或x=2(舍去).x=-2时,y=1;x=-1时,y=12;x=1时,y=-8. ∴ymax=12,ymin=-8.故选A. 5.D6.答案为:A;解析:y′=4x3-4x,令y′<0,即4x3-4x<0,解得x<-1或0<x<1,所以函数的单调递减区间为(-∞,-1)和(0,1),故应选A. 7.答案为:A;解析:在(0,+∞)上,f′(x)=+>0,所以f(x)在(0,+∞)上是增函数,所以有f(2)<f(e)<f(3). 8.答案为:D.解析:因为f(x)=kx-ln x,所以f′(x)=k-x-1.因为f(x)在区间(1,+∞)上单调递增,所以当x>1时,f′(x)=k-x-1≥0恒成立,即k≥x-1在区间(1,+∞)上恒成立.因为x>1,所以0<x-1<1,所以k≥1.故选D. 9.答案为:A;解析:在(0,+∞)内,f′(x)=+>0,所以f(x)在(0,+∞)内是增函数,所以有f(2)<f(e)<f(3). 10.答案为:B;解析:∵f′(x)=3x2-3a,令f′(x)=0,可得a=x2,又∵x∈(0,1),∴0<a<1,故选B. 11.B 12.答案为:B;解析:∵f(x)=x3+ax-2在[1,+∞)上是增函数,∴f′(x)=3x2+a≥0在[1,+∞)上恒成立,即a≥-3x2在[1,+∞)上恒成立,又∵在[1,+∞)上(-3x2)max=-3,∴a≥-3. 二 、填空题13.答案为:(-1,+∞);解析:设g(x)=f(x)-2x-4,则g′(x)=f′(x)-2.∵对任意x∈R,f′(x)>2,∴g′(x)>0. ∴g(x)在R上为增函数.又g(-1)=f(-1)+2-4=0,∴x>-1时,g(x)>0.∴由f(x)>2x+4,得x>-1. 14.答案为:∪[1,+∞);解析:f′(x)=-4x+,若函数f(x)在[1,2]上为单调函数,即f′(x)=-4x+≥0或f′(x)=-4x+≤0在[1,2]上恒成立,即≥4x-或≤4x-在[1,2]上恒成立.令h(x)=4x-,则h(x)在[1,2]上单调递增,所以≥h(2)或≤h(1),即≥或≤3,又a>0,所以0<a≤或a≥1. 15.答案为:(-∞,+∞);解析:因为f′(x)=-sin x+>0,所以f(x)在R上为增函数. 16.答案为:4;解析:∵f′(x)=3x2+6ax+3b,∴⇒∴f′(x)=3x2-6x,令3x2-6x=0,得x=0或x=2,∴f(x)极大值-f(x)极小值=f(0)-f(2)=4. 三 、解答题17.解:f′(x)=3(x2-a)(a≠0),当a<0时,f′(x)>0恒成立,即函数在(-∞,+∞)上单调递增,此时函数没有极值点.当a>0时,令f′(x)=0,得x1=,x2=-,当x变化时,f′(x)与f(x)的变化如下表: 因此,函数f(x)的单调递增区间为(-∞,-)和(,+∞),单调递减区间为(-,),此时x=-是f(x)的极大值点,x=是f(x)的极小值点. 18.解:(1)依题意可知点P(1,f(1))为切点,代入切线方程y=3x+1可得,f(1)=3×1+1=4,∴f(1)=1+a+b+5=4,即a+b=-2,又由f(x)=x3+ax2+bx+5得,又f′(x)=3x2+2ax+b,而由切线y=3x+1的斜率可知f′(1)=3,∴3+2a+b=3,即2a+b=0,由解得∴a=2,b=-4.(2)由(1)知f(x)=x3+2x2-4x+5,f′(x)=3x2+4x-4=(3x-2)(x+2),令f′(x)=0,得x=或x=-2.当x变化时,f(x),f′(x)的变化情况如下表:
因此,函数f(x)的单调递增区间为(-∞,-)和(,+∞),单调递减区间为(-,),此时x=-是f(x)的极大值点,x=是f(x)的极小值点. 18.解:(1)依题意可知点P(1,f(1))为切点,代入切线方程y=3x+1可得,f(1)=3×1+1=4,∴f(1)=1+a+b+5=4,即a+b=-2,又由f(x)=x3+ax2+bx+5得,又f′(x)=3x2+2ax+b,而由切线y=3x+1的斜率可知f′(1)=3,∴3+2a+b=3,即2a+b=0,由解得∴a=2,b=-4.(2)由(1)知f(x)=x3+2x2-4x+5,f′(x)=3x2+4x-4=(3x-2)(x+2),令f′(x)=0,得x=或x=-2.当x变化时,f(x),f′(x)的变化情况如下表: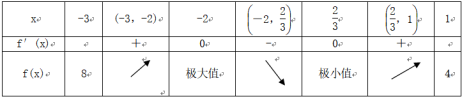 ∴f(x)的极大值为f(-2)=13,极小值为f=,又f(-3)=8,f(1)=4,∴f(x)在[-3,1]上的最大值为13. 19.解:依题意,显然a≠0.因为f′(x)=3ax2-12ax=3ax(x-4),x∈[-1,2],所以令f′(x)=0,解得x1=0,x2=4(舍去).(1)若a>0,当x变化时,f′(x),f(x)的变化情况如下表:
∴f(x)的极大值为f(-2)=13,极小值为f=,又f(-3)=8,f(1)=4,∴f(x)在[-3,1]上的最大值为13. 19.解:依题意,显然a≠0.因为f′(x)=3ax2-12ax=3ax(x-4),x∈[-1,2],所以令f′(x)=0,解得x1=0,x2=4(舍去).(1)若a>0,当x变化时,f′(x),f(x)的变化情况如下表: 由上表知,当x=0时,f(x)取得最大值,所以f(0)=b=3.又f(2)=-16a+3,f(-1)=-7a+3,故f(-1)>f(2),所以当x=2时,f(x)取得最小值.即-16a+3=-29,a=2.(2)若a<0,当x变化时,f′(x),f(x)的变化情况如下表:
由上表知,当x=0时,f(x)取得最大值,所以f(0)=b=3.又f(2)=-16a+3,f(-1)=-7a+3,故f(-1)>f(2),所以当x=2时,f(x)取得最小值.即-16a+3=-29,a=2.(2)若a<0,当x变化时,f′(x),f(x)的变化情况如下表: 所以当x=0时,f(x)取得最小值,所以f(0)=b=-29.又f(2)=-16a-29,f(-1)=-7a-29,故f(2)>f(-1).所以当x=2时,f(x)取得最大值.即-16a-29=3,a=-2.综上所述,所求a,b的值为或 20.解:(1)f′(x)=3x2+2ax+b.由题意,得即解得(2)由(1)知f′(x)=3x2+3x-6=3(x+2)(x-1).令f′(x)=0,得x=-2或x=1.当x变化时,f′(x),f(x)变化情况如下表所示:
所以当x=0时,f(x)取得最小值,所以f(0)=b=-29.又f(2)=-16a-29,f(-1)=-7a-29,故f(2)>f(-1).所以当x=2时,f(x)取得最大值.即-16a-29=3,a=-2.综上所述,所求a,b的值为或 20.解:(1)f′(x)=3x2+2ax+b.由题意,得即解得(2)由(1)知f′(x)=3x2+3x-6=3(x+2)(x-1).令f′(x)=0,得x=-2或x=1.当x变化时,f′(x),f(x)变化情况如下表所示: ∴f(x)在[-3,2]上的最小值为c-.即-<c-解得<c<0或c>.即c的取值范围为∪.
∴f(x)在[-3,2]上的最小值为c-.即-<c-解得<c<0或c>.即c的取值范围为∪.
相关试卷
这是一份高考数学一轮复习夯基练习:指数与指数函数(含答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高考数学一轮复习夯基练习:集合(含答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高考数学一轮复习夯基练习:函数的图象(含答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









