高考数学一轮复习夯基练习：对数与对数函数(含答案)

这是一份高考数学一轮复习夯基练习：对数与对数函数(含答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
夯基练习 对数与对数函数一 、选择题1.已知函数，若实数x0是方程f(x0)=0解，且0＜x1＜x0，则f(x1)值(　　)A.等于0                     B.恒为负值                     C.恒为正值                      D.不能确定2.已知f(2x＋1)=，则f(4)等于(　　)A.log25     B.log23          C.           D. 3.下列各项中表示同一个函数的是(　　)A.y=log2x与y=log2x2　          B.y=10lgx与y=lg10xC.y=x与y=xlogxx               D.y=x与y=lnex  4.已知函数f(x)=log2(x＋1)，若f(a)=1，则a=(　　)A.0          B.1          C.2           D.3  5.函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是 ( 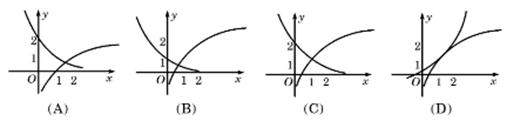   )6.log2353可以化简为(　　)A.log25        B.log52       C.log85        D.log2125  7.已知|lga|=lgb(a>0，b>0)，那么(　　)A.a=b       B.a=b或ab=1       C.a=±b       D.ab=1 8.若对数log(x－1)(4x－5)有意义，则x的取值范围(　　)A.≤x＜2        B.＜x＜2     C.＜x＜2或x＞2     D.x＞  9.若函数f(x)=ax＋loga(x＋1)在[0,1]上的最大值和最小值之和为a，则函数g(x)=ax2＋x＋1在 [－2,2]上的值域为(　　)A.[，5]       B.[－，5]      C.[－，3]       D.[0,3] 10.当a>0，a≠1时，下列说法正确的是(　　)①若M=N，则logaM=logaN；②若logaM=logaN，则M=N；③若logaM2=logaN2，则M=N；④若M=N，则logaM2=logaN2.A.①与②       B.②与④        C.②        D.①②③④ 11.已知，且等于（      ）A、         B、         C、      D、12.设方程lg2x＋(lg2＋lg3)lgx＋lg2·lg3=0的两根为x1，x2，那么x1·x2的值为(　　)A.lg2·lg3       B.lg2＋lg3         C.          D.－6  二 、填空题13.比较大小：(1)log22________log2；(2)log0.50.6________log0.50.4.  14.若log5·log36·log6x=2，则x等于________. 15.函数y=的递增区间是16.已知2m=5n=10，则＋=________.   三 、解答题17.若log2[log0.5(log2x)]=0，求x的值.      18.计算： ；     19.已知f(x)=loga(1－x)＋loga(x＋3)，(a>0且a≠1).(1)求函数f(x)的定义域，值域；(2)若函数f(x)有最小值为－2，求a的值.       20.已知函数为奇函数，a为常数.(1)确定a的值；(2)求证：f(x)是(1,+∞)上的增函数；(3)若对于区间[3,4]上的每一个x值，不等式f(x)>(0.5)x+m恒成立，求实数m取值范围.       
参考答案1.C.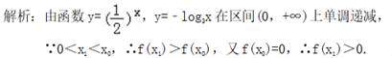                                          2.答案为：B；解析：令2x＋1=4，得x=log23，所以f(4)=log23，选B. 3.答案为：D；  4.答案为：B；解析：f(a)=log2(a＋1)=1，所以a＋1=2，所以a=1.  5.答案为：C.6.答案为：A；  7.答案为：B 8.答案为：C；  9.答案为：A解析：显然函数f(x)=ax＋loga(x＋1)在[0,1]上是单调的，∴函数f(x)在[0,1]上的最大值和最小值之和为f(0)＋f(1)=1＋a＋loga2=a，解得a=.∴g(x)=x2＋x＋1在[－2，－1]上单调递减，在[－1,2]上单调递增.∴g(x)=x2＋x＋1在[－2,2]上的值域为[，5].故选A. 10.答案为：C 11.D；12.答案为：C解析：设lgx=t，则t2＋(lg2＋lg3)t＋lg2lg3=0.据又t1＋t2=－lg2－lg3=lgx1＋lgx2，∴x1x2=.  二 、填空题13.答案为：(1)>，(2)<；解析：(1)因为函数y=log2x在(0，＋∞)上是增函数，且2>，所以log22>log2.(2)因为函数y=log0.5x在(0，＋∞)上是减函数，且0.6>0.4，所以log0.50.6<log0.50.4.  14.答案为：解析：由换底公式，得··=2，lg x=－2lg 5，x=5－2=. 15.16.答案为：1；   三 、解答题17.解：由条件知log0.5(log2x)=1=log0.50.5，得log2x==log2，从而x=.  18.答案为：0.19.解：(1)∵∴定义域为{x|－3<x<1}.f(x)=loga(－x2－2x＋3)，令t=－x2－2x＋3=－(x＋1)2＋4，∵x∈(－3，1)，∴t∈(0，4].∴f(t)=logat，t∈(0，4].当0<a<1时，ymin=f(4)=loga4，值域为[loga4，＋∞).当a>1时，ymax=f(4)=loga4，值域为(－∞，loga4].(2)∵ymin=－2，由①得得a=. 20.解：