


高考数学一轮复习夯基练习:函数y=Asin(ωx+φ)的图象及应用(含答案)
展开夯基练习 函数 y=Asin(ωx+φ)的图象及应用
1.为了得到函数y=sin(x+1)的图象,只需把函数y=sin x的图象上所有的点( )
A.向左平行移动1个单位长度
B.向右平行移动1个单位长度
C.向左平行移动π个单位长度
D.向右平行移动π个单位长度
A.![]()
B.![]()
C.![]()
D.![]() ∪
∪![]()
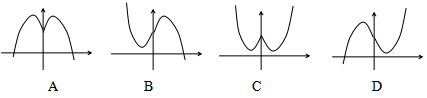
A.![]() B.
B.![]() C.sin2x D.cos2x
C.sin2x D.cos2x
A. [kπ-, kπ+] (k∈Z) B. [kπ+, kπ+] (k∈Z)
C. [kπ-, kπ+] (k∈Z) D. [kπ+, kπ+] (k∈Z)
6.已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<![]() )的图象如图所示,则函数f(x)的解析式是( )
)的图象如图所示,则函数f(x)的解析式是( )
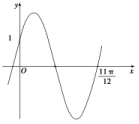
A.f(x)=2sin(![]() x+
x+![]() ) B.f(x)=2sin(
) B.f(x)=2sin(![]() x-
x-![]() )
)
C.f(x)=2sin(2x+![]() ) D.f(x)=2sin(2x-
) D.f(x)=2sin(2x-![]() )
)
A.向左平移![]() 个单位 B.同右平移
个单位 B.同右平移![]() 个单位
个单位
C.向左平移![]() 个单位 D.向右平移
个单位 D.向右平移![]() 个单位
个单位
8.函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asin ωx的图象,只需将函数y=f(x)的图象( )
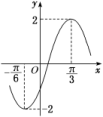
A.向左平移个单位长度 B.向左平移个单位长度
C.向右平移个单位长度 D.向右平移个单位长度
9.函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<)的图象如图所示,为了得到g(x)=sin 2x的图象,则只要将f(x)的图象( )

A.向右平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向左平移个单位长度
10.函数f(x)=sin(2x+φ)为R上的奇函数,则φ的值可以是( )
A. B. C.π D.
11.将函数y=3sin(2x+)的图象向右平移个单位长度,所得图象对应的函数( )
A.在区间[,]上单调递减
B.在区间[,]上单调递增
C.在区间[-,]上单调递减
D.在区间[-,]上单调递增
12.将函数f(x)=2sin的图象向左平移个单位长度,再向上平移1个单位长度,得到g(x)的图象,若g(x1)·g(x2)=9,且x1,x2∈[-2π,2π],则2x1-x2的最大值为( )
A. B. C. D.
13.设a= log![]() tan70°, b=log
tan70°, b=log![]() sin25°,c=(
sin25°,c=(![]() )cos25°,则它们的大小关系为_________.
)cos25°,则它们的大小关系为_________.
14.如果函数 y=sin2x+acos2x 的图象关于直线x=-对称,那么a=_________.
15.若将某正弦函数的图象向右平移![]() 个单位长度以后,所得到的图象的函数式是y=sin(x+
个单位长度以后,所得到的图象的函数式是y=sin(x+![]() ),则原来的函数表达式为________.
),则原来的函数表达式为________.
16.已知简谐运动f(x)=2sin(![]() )(|φ|<)的图象经过点(0,1),则该简谐运动的最小正周期T和初相φ分别为:T=________,φ=________.
)(|φ|<)的图象经过点(0,1),则该简谐运动的最小正周期T和初相φ分别为:T=________,φ=________.
17.使函数y=f(x)图象上每一点的纵坐标保持不变,横坐标缩小到原来的![]() 倍,然后再将其图象沿x轴向左平移
倍,然后再将其图象沿x轴向左平移![]() 个单位得到的曲线与y=sin 2x的图象相同,求f(x)的表达式.
个单位得到的曲线与y=sin 2x的图象相同,求f(x)的表达式.
(1)求实数k的范围;
(2)若k∈N+,当k取最小值时,![]() ①求函数f(x)的最大值及相应x的取值集合;②求函数f(x)的对称中心.
①求函数f(x)的最大值及相应x的取值集合;②求函数f(x)的对称中心.
(1)试说明y=f(x)的图象由函数y=sin x的图象经过怎样的变化得到;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,当x∈[0,1]时,求函数y=g(x)的最值.
(1)求f(x)的最大值和最小值;
(2)若不等式f(x)-m<2在x∈[![]() ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
解析:只需把函数y=sin x的图象上所有的点向左平行移动1个单位长度,
便得函数y=sin(x+1)的图象,故选A.
解析:由题图知A=2,=-=,∴T=π,∴ω=2,∴f(x)=2cos(2x+φ),
将代入得cos=1,∵-π<φ<0,∴-<+φ<,
∴+φ=0,∴φ=-,∴f(x)=2cos=2sin,
故将函数y=f(x)的图象向左平移个单位长度可得到g(x)的图象.
解析:由题图可知,A=1,T=4=π,故ω==2,由于(,0)为五点作图的第三点,
∴2×+φ=π,解得φ=,所以f(x)=sin(2x+),
将函数f(x)的图象向右平移个单位长度,得y=sin=sin 2x=g(x),故选A.
解析:要使函数f(x)=sin(2x+φ)为R上的奇函数,需φ=kπ,k∈Z.故选C.
将函数y=3sin(2x+)的图象向右平移个单位长度,
得到y=3sin[2(x-)+]=3sin(2x-),
令2kπ-≤2x-≤2kπ+,k∈Z,解得kπ+≤x≤kπ+,k∈Z,
故递增区间为[kπ+,kπ+](k∈Z),当k=0时,得递增区间为[,],故选B.
解析:由题意可得,g(x)=2sin+1,所以g(x)max=3,又g(x1)·g(x2)=9,
所以g(x1)=g(x2)=3,由g(x)=2sin+1=3,得2x+=+2kπ(k∈Z),
即x=+kπ(k∈Z),因为x1,x2∈[-2π,2π],
所以(2x1-x2)max=2×-=,故选B.
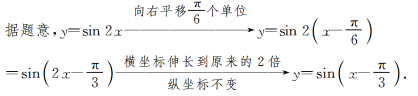
(2)①![]() 时,f(x)max=4;②
时,f(x)max=4;②![]() (n∈Z)
(n∈Z)
(1)∵函数f(x)=sin-2cos2=sin xcos -cos xsin -cos x-1
=sin x-cos x-1=sin-1,
∴把函数y=sin 的图象向先右平移1个单位长度,再向下平移1个单位长度,
得到函数y=f(x)的图象.
(2)∵函数y=g(x)与y=f(x)的图象关于直线x=2对称,
∴g(x)=f(4-x)=sin-1=sin x-1.
当x∈[0,1]时,x∈,故当x=0时,函数y=g(x)取得最小值-1;
当x=1时,函数y=g(x)取得最大值.

高考数学一轮复习 专题5.5 函数y=Asin(ωx+φ)的图象及其应用(练): 这是一份高考数学一轮复习 专题5.5 函数y=Asin(ωx+φ)的图象及其应用(练),文件包含专题55函数y=Asinωx+φ的图象及其应用练教师版docx、专题55函数y=Asinωx+φ的图象及其应用练学生版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。
高考数学一轮复习 专题5.5 函数y=Asin(ωx+φ)的图象及其应用(讲): 这是一份高考数学一轮复习 专题5.5 函数y=Asin(ωx+φ)的图象及其应用(讲),文件包含专题55函数y=Asinωx+φ的图象及其应用讲教师版docx、专题55函数y=Asinωx+φ的图象及其应用讲学生版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
高中数学复习专题:函数y=Asin(ωx+φ)的图象及应用: 这是一份高中数学复习专题:函数y=Asin(ωx+φ)的图象及应用,共21页。试卷主要包含了y=Asin的有关概念等内容,欢迎下载使用。












