


高考数学一轮复习夯基练习:函数的图象(含答案)
展开夯基练习 函数的图象
2.已知函数f(x)是定义在R上的奇函数,且当x≥0时,f(x)=log2(x+2)-1,则f(-6)=( )
A.2 B.4 C.-2 D.-4
3.已知函数f(x)=x|x|-2x,则下列结论正确的是( )
A.f(x)是偶函数,递增区间是(0,+∞)
B.f(x)是偶函数,递减区间是(-∞,1)
C.f(x)是奇函数,递减区间是(-1,1)
D.f(x)是奇函数,递增区间是(-∞,0)
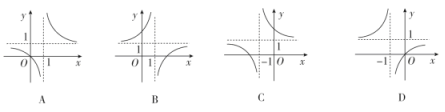
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于y=x对称
x | 1 | 0.5 |
f(x) | 1 |
|
则不等式f(|x|)≤2的解集是( )
A.{x|-4≤x≤4} B.{x|0≤x≤4} C.{x|-![]() ≤x≤
≤x≤![]() } D.{x|0<x≤
} D.{x|0<x≤![]() }
}
7.已知函数y=f(x)的图象过点(1,1),那么f(4-x)的图象一定经过点( )
A.(1,4) B.(4,1) C.(3,1) D.(1,3)
8.已知定义在R上的奇函数f(x)满足f(x+2)+f(x)=0且当x∈[0,1]时,f(x)=log2(x+1),则下列不等式正确的是( )
A.f(log27)<f(-5)<f(6) B.f(log27)<f(6)<f(-5)
C.f(-5)<f(log27)<f(6) D.f(-5)<f(6)<f(log27)
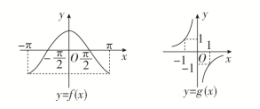
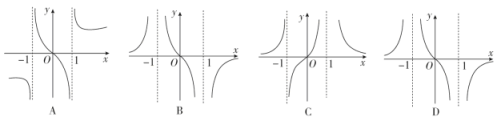
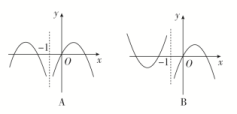
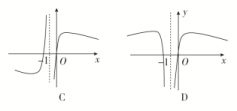
9.函数y=f(x)与y=g(x)的图象如图所示,则函数y=f(x)·g(x)的图象可能为( )

14.若x≥0,y≥0,且x+2y=1,则2x+3y2的最小值为 .
15.给定min{a,b}=已知函数f(x)=min{x,x2-4x+4}+4,若动直线y=m与函数y=f(x)的图象有3个交点,则实数m的取值范围为________.
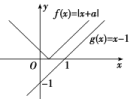
16.设函数f(x)=|x+a|,g(x)=x-1,对于任意的x∈R,不等式f(x)≥g(x)恒成立,则实数a的取值范围是________.
f(x)=
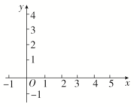
(1)在如图所示给定的直角坐标系内画出f(x)的图象;
(2)写出f(x)的单调递增区间;
(3)由图象指出当x取什么值时f(x)有最值.
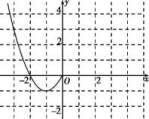
18.已知函数f(x)是定义在R上的偶函数,且当x≤0时, f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示.
(1)写出函数f(x)(x∈R)的增区间;
(2)写出函数f(x)(x∈R)的解析式;
(3)若函数g(x)=f(x)-2ax+2(x∈[1,2]),求函数g(x)的最小值.
19.已知函数h(x)=(m2-5m+1)xm+1为幂函数,且为奇函数.
(1)求m的值;
(2)求函数g(x)=h(x)+![]() ,x∈[0,0.5]的值域.
,x∈[0,0.5]的值域.
20.已知函数f(x)=|x2-4x+3|.若关于x的方程f(x)-a=x至少有三个不相等的实数根,求实数a的取值范围.
解析:由题意,知f(-6)=-f(6)=-(log28-1)=-3+1=-2,故选C.
解析:选C.将函数f(x)=x|x|-2x去掉绝对值得f(x)=
画出函数f(x)的图象,如图,观察图象可知,函数f(x)的图象关于原点对称,
故函数f(x)为奇函数,且在(-1,1)上单调递减.
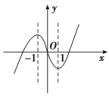
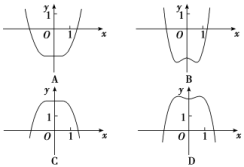
解析:选D.
令y=f(x)=-x4+x2+2,则f′(x)=-4x3+2x,当x<-或0<x<时,f′(x)>0,f(x)递增;当-<x<0或x>时,f′(x)<0,f(x)递减.由此可得f(x)的图象大致为D中的图象.
故选D.
6.A由题意知![]() =
=![]() ,∴α=0.5,∴f(x)=
,∴α=0.5,∴f(x)=![]() ,由|x
,由|x![]() ≤2,得|x|≤4,故-4≤x≤4.
≤2,得|x|≤4,故-4≤x≤4.
解析:f(x+2)+f(x)=0⇒f(x+2)=-f(x)⇒f(x+4)=-f(x+2)=f(x),
所以f(x)是周期为4的周期函数.
又f(-x)=-f(x),且有f(2)=-f(0)=0,
所以f(-5)=-f(5)=-f(1)=-log22=-1,f(6)=f(2)=0.
又2<log27<3,所以0<log27-2<1,即0<log2<1,
f(log27)+f(log27-2)=0⇒f(log27)=-f(log27-2)=-f
=-log2=-log2,又1<log2<2,
所以0<log2<1,所以-1<-log2<0,
所以f(-5)<f(log27)<f(6).
解析:
由两函数的图象可知当x∈-π,-时,y=f(x)·g(x)<0;当x∈-,0时,y=f(x)·g(x)>0;
当x∈0,时,y=f(x)·g(x)<0;当x∈,π时,y=f(x)·g(x)>0,
观察各选项只有A项符合题意,故选A.
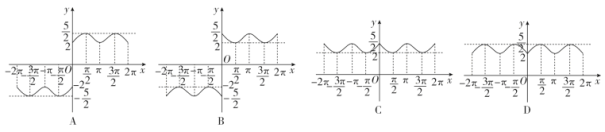
解析:
因为f(-x)=2sin(-x)+=+2sinx=f(x),所以函数f(x)=2sinx+是定义在R上的偶函数,
排除A,B;又f=2sin+=2+=,排除C.
综上,函数f(x)=2sinx+的部分图象应为D,故选D.
解析:当x>1时,y>0,故排除B,D;当x<-1时,y<0,故排除C,故选A.
解析:
当-1-<x<-1时,10ln |x+1|<0,x+1<0,从而y>0,故排除A,D两项.
当x→-∞时,10ln |x+1|>0,x+1<0,从而y<0,故可排除B项,故选C.
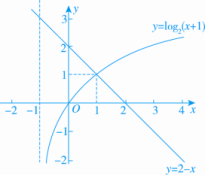
解析:画出y=2-x,y=log2(x+1)的图象如图所示,由图可知,解集为{x|x≥1}.
14.答案0.75解析 由x≥0,且x+2y=1得x=1-2y≥0,又y≥0,∴0≤y≤![]() ,设t=2x+3y2,把x=1-2y代入,得t=2-4y+3y2=3
,设t=2x+3y2,把x=1-2y代入,得t=2-4y+3y2=3![]() +
+![]() ,∴t=2-4y+3y2在
,∴t=2-4y+3y2在![]() 上递减,∴当y=
上递减,∴当y=![]() 时,t取到最小值,即tmin=
时,t取到最小值,即tmin=![]() .
.
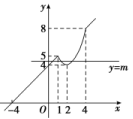
解析:作函数f(x)=min{x,x2-4x+4}+4=的图象如图所示,
由于直线y=m与函数y=f(x)的图象有3个交点,数形结合可得m的取值范围为(4,5).
解析:如图,作出函数f(x)=|x+a|与g(x)=x-1的图象,观察图象可知:当且仅当-a≤1,
即a≥-1时,不等式f(x)≥g(x)恒成立,因此a的取值范围是[-1,+∞).
(1)函数f(x)的图象如图所示.
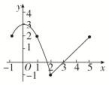
(2)由图象可知,函数f(x)的单调递增区间为[-1,0],[2,5].
(3)由图象知当x=2时,f(x)min=f(2)=-1,
当x=0时,f(x)max=f(0)=3.
18.解析 (1)f(x)的增区间为(-1,0),(1,+∞).
(2)若x>0,则-x<0,又函数f(x)是定义在R上的偶函数,且当x≤0时, f(x)=x2+2x,
∴f(x)=f(-x)=(-x)2+2×(-x)=x2-2x(x>0),∴f(x)=![]()
(3)g(x)=x2-2x-2ax+2,其图象的对称轴方程为x=a+1,
当a+1≤1,即a≤0时,g(1)=1-2a为g(x)在[1,2]上的最小值;
当1<a+1≤2,即0<a≤1时,g(a+1)=-a2-2a+1为g(x)在[1,2]上的最小值;
当a+1>2,即a>1时,g(2)=2-4a为g(x)在[1,2]上的最小值.
综上,在x∈[1,2]上,g(x)min=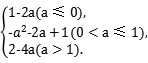
(1)∵函数h(x)=(m2-5m+1)xm+1为幂函数,
∴m2-5m+1=1,解得m=0或5,
又h(x)为奇函数,
∴m=0.
(2)由(1)可知g(x)=x+![]() ,x∈
,x∈![]() ,令
,令![]() =t,
=t,
则t∈[0,1],
∴f(t)=-![]() t2+t+
t2+t+![]() =-
=-![]() (t-1)2+1,t∈[0,1],
(t-1)2+1,t∈[0,1],
则f(t)∈![]() ,
,
即g(x)=h(x)+![]() ,x∈
,x∈![]() 的值域为
的值域为![]() .
.
f(x)=
作出图象如图所示.
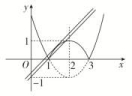
原方程变形为|x2-4x+3|=x+a.
于是,设y=x+a,在同一坐标系下再作出y=x+a的图象(如图).
则当直线y=x+a过点(1,0)时,a=-1;
当直线y=x+a与抛物线y=-x2+4x-3相切时,
由⇒x2-3x+a+3=0.
由Δ=9-4(3+a)=0,得a=-.
由图象知当a∈时方程至少有三个不等实根.
高考数学一轮复习夯基练习:圆的方程(含答案): 这是一份高考数学一轮复习夯基练习:圆的方程(含答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
高考数学一轮复习夯基练习:椭圆(含答案): 这是一份高考数学一轮复习夯基练习:椭圆(含答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
高考数学一轮复习夯基练习:随机抽样(含答案): 这是一份高考数学一轮复习夯基练习:随机抽样(含答案),共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












