


所属成套资源:高考数学一轮复习夯基练习 (含答案)
高考数学一轮复习夯基练习:抛物线(含答案)
展开
这是一份高考数学一轮复习夯基练习:抛物线(含答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
夯基练习 抛物线一 、选择题1.若点A,B在抛物线y2=2px(p>0)上,O是坐标原点,若正三角形OAB的面积为4,则该抛物线方程是( )A.y2=x B.y2=x C.y2=2x D.y2=x 2.已知点A(-2,3)在抛物线C:y2=2px(p>0)的准线上,记C的焦点为F,则直线AF的斜率为( )A.- B.-1 C.- D.- 3.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点.若=4,则|QF|等于( )A.3.5 B.2.5 C.3 D.2 4.到定点A(2,0)与定直线l:x=-2的距离相等的点的轨迹方程为( )A.y2=8x B.y2=-8x C.x2=8y D.x2=-8y 5.设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )A.(0,2) B.[0,2] C.(2,+∞) D.[2,+∞) 6.设抛物线的顶点在原点,准线方程为x=-2,则抛物线的方程是( )A.y2=-8x B.y2=-4x C.y2=8x D.y2=4x 7.过抛物线x2=4y的焦点F作直线l交抛物线于P1(x1,y1),P2(x2,y2)两点,若y1+y2=6,则|P1P2|=( )A.5 B.6 C.8 D.10 8.过抛物线y2=4x的焦点作直线交抛物线于A,B两点,若O为坐标原点,则![]()
![]() =( ) A.﹣1 B.﹣2 C.﹣3 D.﹣49.已知双曲线-=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )A.2 B.2 C.4 D.4 10.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点.若
=( ) A.﹣1 B.﹣2 C.﹣3 D.﹣49.已知双曲线-=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )A.2 B.2 C.4 D.4 10.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点.若![]() =4
=4![]() ,则|QF|=( ) A.3.5 B.3 C.2.5 D.211.已知抛物线y2=8x,点Q是圆C:x2+y2+2x-8y+13=0上任意一点,记抛物线上任意一点P到直线x=-2的距离为d,则|PQ|+d的最小值为( )A.5 B.4 C.3 D.2 12.已知抛物线y2=2px(p>0)过点A,其准线与x轴交于点B,直线AB与抛物线的另一个交点为M,若=λ,则实数λ为( )A. B. C.2 D.3 二 、填空题13.已知抛物线y2=4x的一条弦AB恰好以P(1,1)为中点,则弦AB所在直线的方程是________. 14.抛物线C:y2=2px(p>0)的焦点为F,点O是坐标原点,过点O,F的圆与抛物线C的准线相切,且该圆的面积为36π,则抛物线的方程为________. 15.已知AB是抛物线2x2=y的焦点弦,若|AB|=4,则AB的中点的纵坐标为________. 16.设P是抛物线y2=4x上的一个动点,则点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值为________. 三 、解答题17.已知抛物线的顶点在原点,焦点在x轴的正半轴上,抛物线上的点M(3,m)到焦点的距离等于5,求抛物线的方程和m的值. 18.证明:以抛物线的焦点弦为直径的圆与抛物线的准线相切. 19.已知抛物线的顶点在原点,焦点在y轴上,抛物线上一点M(m,-3)到焦点的距离为5,求m的值、抛物线方程和准线方程. 20.已知抛物线C:y2=2px经过点P(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.(1)求直线l的斜率的取值范围;(2)设O为原点,=λ,=μ,求证:+为定值.
,则|QF|=( ) A.3.5 B.3 C.2.5 D.211.已知抛物线y2=8x,点Q是圆C:x2+y2+2x-8y+13=0上任意一点,记抛物线上任意一点P到直线x=-2的距离为d,则|PQ|+d的最小值为( )A.5 B.4 C.3 D.2 12.已知抛物线y2=2px(p>0)过点A,其准线与x轴交于点B,直线AB与抛物线的另一个交点为M,若=λ,则实数λ为( )A. B. C.2 D.3 二 、填空题13.已知抛物线y2=4x的一条弦AB恰好以P(1,1)为中点,则弦AB所在直线的方程是________. 14.抛物线C:y2=2px(p>0)的焦点为F,点O是坐标原点,过点O,F的圆与抛物线C的准线相切,且该圆的面积为36π,则抛物线的方程为________. 15.已知AB是抛物线2x2=y的焦点弦,若|AB|=4,则AB的中点的纵坐标为________. 16.设P是抛物线y2=4x上的一个动点,则点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值为________. 三 、解答题17.已知抛物线的顶点在原点,焦点在x轴的正半轴上,抛物线上的点M(3,m)到焦点的距离等于5,求抛物线的方程和m的值. 18.证明:以抛物线的焦点弦为直径的圆与抛物线的准线相切. 19.已知抛物线的顶点在原点,焦点在y轴上,抛物线上一点M(m,-3)到焦点的距离为5,求m的值、抛物线方程和准线方程. 20.已知抛物线C:y2=2px经过点P(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.(1)求直线l的斜率的取值范围;(2)设O为原点,=λ,=μ,求证:+为定值.
参考答案1.答案为:A.解析:根据抛物线的对称性,AB⊥x轴,由于正三角形的面积是4,故AB2=4,故AB=4,正三角形的高为2,故可以设点A的坐标为(2,2)代入抛物线方程得4=4p,解得p=,故所求的抛物线方程为y2=x.故选A. 2.答案为:C.解析:由已知,得准线方程为x=-2,所以F的坐标为(2,0).又A(-2,3),所以直线AF的斜率为k==-. 3.答案为:C.解析:因为=4,所以||=4||,所以=.如图,过Q作QQ′⊥l,垂足为Q′,设l与x轴的交点为A,则|AF|=4,所以==,所以|QQ′|=3,根据抛物线定义可知|QQ′|=|QF|=3. 4.答案为:A;解析:由抛物线的定义可知该轨迹为抛物线且p=4,焦点在x轴正半轴上,故选A. 5.答案为:C;解析:圆心到抛物线准线的距离为p,即4,根据已知只要|FM|>4即可.根据抛物线定义,|FM|=y0+2,由y0+2>4,解得y0>2,故y0的取值范围是(2,+∞). 6.答案为:C;解析:显然由准线方程x=-2,可知抛物线为焦点在x轴正半轴上的标准方程,同时得p=4,所以标准方程为y2=2px=8x. 7.答案为:C;解析:由抛物线的定义知|P1P2|=y1+y2+p=6+2=8. 8.C.
4.答案为:A;解析:由抛物线的定义可知该轨迹为抛物线且p=4,焦点在x轴正半轴上,故选A. 5.答案为:C;解析:圆心到抛物线准线的距离为p,即4,根据已知只要|FM|>4即可.根据抛物线定义,|FM|=y0+2,由y0+2>4,解得y0>2,故y0的取值范围是(2,+∞). 6.答案为:C;解析:显然由准线方程x=-2,可知抛物线为焦点在x轴正半轴上的标准方程,同时得p=4,所以标准方程为y2=2px=8x. 7.答案为:C;解析:由抛物线的定义知|P1P2|=y1+y2+p=6+2=8. 8.C.  9.答案为:B;解析:由解得由题得知解得又知+a=4,故a=2,b=1,c==,∴焦距2c=2. 10.答案为:B;
9.答案为:B;解析:由解得由题得知解得又知+a=4,故a=2,b=1,c==,∴焦距2c=2. 10.答案为:B;
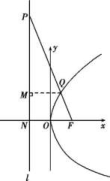 11.答案为:C.解析:如图,由题意知抛物线y2=8x的焦点为F(2,0),连接PF,FQ,则d=|PF|,将圆C的方程化为(x+1)2+(y-4)2=4,圆心为C(-1,4),半径为2,则|PQ|+d=|PQ|+|PF|,又|PQ|+|PF|≥|FQ|(当且仅当F,P,Q三点共线时取得等号).所以当F,Q,C三点共线时取得最小值,且为|CF|-|CQ|=-2=3,故选C.
11.答案为:C.解析:如图,由题意知抛物线y2=8x的焦点为F(2,0),连接PF,FQ,则d=|PF|,将圆C的方程化为(x+1)2+(y-4)2=4,圆心为C(-1,4),半径为2,则|PQ|+d=|PQ|+|PF|,又|PQ|+|PF|≥|FQ|(当且仅当F,P,Q三点共线时取得等号).所以当F,Q,C三点共线时取得最小值,且为|CF|-|CQ|=-2=3,故选C.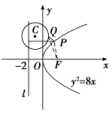 12.答案为:C;把点A代入抛物线的方程得2=2p×,解得p=2,所以抛物线的方程为y2=4x,则B(-1,0),设M,则=,=,由=λ,得解得λ=2或λ=1(舍去),故选C. 二 、填空题13.答案为:2x-y-1=0;解析:设点A(x1,y1),B(x2,y2),由A,B都在抛物线上,可得作差得(y1+y2)(y1-y2)=4(x1-x2).因为AB中点为P(1,1),所以y1+y2=2,则有2·=4,所以kAB==2,从而直线AB的方程为y-1=2(x-1),即2x-y-1=0. 14.答案为:y2=16x;解析:设满足题意的圆的圆心为M.根据题意可知圆心M在抛物线上,又因为圆的面积为36π,所以圆的半径为6,则|MF|=xM+=6,即xM=6-,又由题意可知xM=,所以=6-,解得p=8.所以抛物线方程为y2=16x. 15.答案为:;解析:设AB的中点为P(x0,y0),分别过A,P,B三点作准线的垂线,垂足分别为A′,Q,B′.由题意得|AA′|+|BB′|=|AB|=4,|PQ|==2.又|PQ|=y0+,所以y0+=2,解得y0=. 16.答案为:;解析:如图,易知抛物线的焦点为F(1,0),准线方程是x=-1,由抛物线的定义知,点P到直线x=-1的距离等于点P到F的距离.于是问题转化为在抛物线上求一点P,使点P到点A(-1,1)的距离与点P到F(1,0)的距离之和最小,连接AF交抛物线于点P,此时最小值为|AF|==.
12.答案为:C;把点A代入抛物线的方程得2=2p×,解得p=2,所以抛物线的方程为y2=4x,则B(-1,0),设M,则=,=,由=λ,得解得λ=2或λ=1(舍去),故选C. 二 、填空题13.答案为:2x-y-1=0;解析:设点A(x1,y1),B(x2,y2),由A,B都在抛物线上,可得作差得(y1+y2)(y1-y2)=4(x1-x2).因为AB中点为P(1,1),所以y1+y2=2,则有2·=4,所以kAB==2,从而直线AB的方程为y-1=2(x-1),即2x-y-1=0. 14.答案为:y2=16x;解析:设满足题意的圆的圆心为M.根据题意可知圆心M在抛物线上,又因为圆的面积为36π,所以圆的半径为6,则|MF|=xM+=6,即xM=6-,又由题意可知xM=,所以=6-,解得p=8.所以抛物线方程为y2=16x. 15.答案为:;解析:设AB的中点为P(x0,y0),分别过A,P,B三点作准线的垂线,垂足分别为A′,Q,B′.由题意得|AA′|+|BB′|=|AB|=4,|PQ|==2.又|PQ|=y0+,所以y0+=2,解得y0=. 16.答案为:;解析:如图,易知抛物线的焦点为F(1,0),准线方程是x=-1,由抛物线的定义知,点P到直线x=-1的距离等于点P到F的距离.于是问题转化为在抛物线上求一点P,使点P到点A(-1,1)的距离与点P到F(1,0)的距离之和最小,连接AF交抛物线于点P,此时最小值为|AF|==.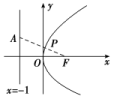 三 、解答题17.解:法一:设抛物线方程为y2=2px(p>0),则焦点F(,0),由题设可得解得或故所求的抛物线方程为y2=8x,m的值为±2.法二:设抛物线方程为y2=2px(p>0),焦点F(,0),准线方程x=-,根据抛物线定义,点M到焦点的距离等于M到准线方程的距离,则3+=5,∴p=4.因此抛物线方程为y2=8x.又点M(3,m)在抛物线上,于是m2=24,∴m=±2.18.证明:如图,设抛物线方程y2=2px(p>0),准线为l,AB为抛物线的焦点弦,点P为AB的中点,
三 、解答题17.解:法一:设抛物线方程为y2=2px(p>0),则焦点F(,0),由题设可得解得或故所求的抛物线方程为y2=8x,m的值为±2.法二:设抛物线方程为y2=2px(p>0),焦点F(,0),准线方程x=-,根据抛物线定义,点M到焦点的距离等于M到准线方程的距离,则3+=5,∴p=4.因此抛物线方程为y2=8x.又点M(3,m)在抛物线上,于是m2=24,∴m=±2.18.证明:如图,设抛物线方程y2=2px(p>0),准线为l,AB为抛物线的焦点弦,点P为AB的中点,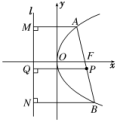 ∴P为以AB为直径的圆的圆心,AM⊥l,BN⊥l,PQ⊥l,垂足分别为M,N,Q.则|AB|=|AF|+|BF|=|AM|+|BN|=2|PQ|,即|PQ|=|AB|,所以以AB为直径的圆必与准线相切.即得证. 19.解:法一:设所求抛物线方程为x2=-2py(p>0),则焦点坐标为F.∵M(m,-3)在抛物线上,且|MF|=5,故解得∴抛物线方程为x2=-8y,m=±2,准线方程为y=2.法二:如图所示,设抛物线方程为x2=-2py(p>0),
∴P为以AB为直径的圆的圆心,AM⊥l,BN⊥l,PQ⊥l,垂足分别为M,N,Q.则|AB|=|AF|+|BF|=|AM|+|BN|=2|PQ|,即|PQ|=|AB|,所以以AB为直径的圆必与准线相切.即得证. 19.解:法一:设所求抛物线方程为x2=-2py(p>0),则焦点坐标为F.∵M(m,-3)在抛物线上,且|MF|=5,故解得∴抛物线方程为x2=-8y,m=±2,准线方程为y=2.法二:如图所示,设抛物线方程为x2=-2py(p>0),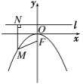 则焦点F,准线l:y=,又|MF|=5,由定义知3+=5,∴p=4.∴抛物线方程为x2=-8y,准线方程为y=2.由m2=(-8)×(-3),得m=±2. 20.解:(1)因为抛物线y2=2px过点(1,2),所以2p=4,即p=2.故抛物线C的方程为y2=4x,由题意知,直线l的斜率存在且不为0.设直线l的方程为y=kx+1(k≠0).由得k2x2+(2k-4)x+1=0.依题意Δ=(2k-4)2-4×k2×1>0,解得k<0或0<k<1.又PA,PB与y轴相交,故直线l不过点(1,-2).从而k≠-3.所以直线l斜率的取值范围是(-∞,-3)∪(-3,0)∪(0,1).(2)证明:设A(x1,y1),B(x2,y2),由(1)知x1+x2=-,x1x2=.直线PA的方程为y-2=(x-1).令x=0,得点M的纵坐标为yM=+2=+2.同理得点N的纵坐标为yN=+2.由=λ,=μ得λ=1-yM,μ=1-yN.所以+=+=+=·=·=2.所以+为定值.
则焦点F,准线l:y=,又|MF|=5,由定义知3+=5,∴p=4.∴抛物线方程为x2=-8y,准线方程为y=2.由m2=(-8)×(-3),得m=±2. 20.解:(1)因为抛物线y2=2px过点(1,2),所以2p=4,即p=2.故抛物线C的方程为y2=4x,由题意知,直线l的斜率存在且不为0.设直线l的方程为y=kx+1(k≠0).由得k2x2+(2k-4)x+1=0.依题意Δ=(2k-4)2-4×k2×1>0,解得k<0或0<k<1.又PA,PB与y轴相交,故直线l不过点(1,-2).从而k≠-3.所以直线l斜率的取值范围是(-∞,-3)∪(-3,0)∪(0,1).(2)证明:设A(x1,y1),B(x2,y2),由(1)知x1+x2=-,x1x2=.直线PA的方程为y-2=(x-1).令x=0,得点M的纵坐标为yM=+2=+2.同理得点N的纵坐标为yN=+2.由=λ,=μ得λ=1-yM,μ=1-yN.所以+=+=+=·=·=2.所以+为定值.
相关试卷
这是一份高考数学一轮复习夯基练习:圆的方程(含答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高考数学一轮复习夯基练习:椭圆(含答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高考数学一轮复习夯基练习:随机抽样(含答案),共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









