高考数学一轮复习夯基练习：双曲线(含答案)

夯基练习 双曲线

一 、选择题

1.若实数k满足0<k<5，则曲线与曲线的(　　)

A.实半轴长相等        B.虚半轴长相等      C.离心率相等          D.焦距相等

2.双曲线-=1(a>0，b>0)的离心率为，则其渐近线方程为(　　)

A．y=±x        B．y=±x         C．y=±x        D．y=±x

3.若双曲线－=1(a＞0，b＞0)的一条渐近线方程为y=－2x，则该双曲线的离心率是(　　)

A．           B．        C．           D．2

4.已知双曲线C：-=1(a>0，b>0)的焦距为10，点P(2，1)在C的渐近线上，则C的方程为(　　)

A．-=1        B．-=1        C．-=1        D．-=1

5.设动点P到A(-5，0)的距离与它到B(5，0)距离的差等于6，则P点的轨迹方程是(　　)

A.      B.   

C.(x≤-3)     D.(x≥3)

6.若双曲线E：=1的左、右焦点分别为F1，F2，点P在双曲线E上，且|PF1|=3，则|PF2|等于(  )

A.11           B.9                          C.5                           D.3

7.已知点F为双曲线E：-=1(a>0，b>0)的右焦点，直线y=kx(k>0)与E交于不同象限内的M，N两点，若MF⊥NF，设∠MNF=β，且β∈，，则该双曲线的离心率的取值范围是(　　)

A．[，＋]    B．[2，＋1]     C．[2，＋]    D．[，＋1]

8.设F1，F2分别为双曲线(a>0，b>0)的左、右焦点.若在双曲线右支上存在点P，

满足|PF2|=|F1F2|，且F2到直线PF1的距离等于双曲线实轴长，则该双曲线渐近线方程为(　　)

A.3x±4y=0       B.3x＋5y=0      C.5x±4y=0      D.4x±3y=0

9.已知O为坐标原点，设F1，F2分别是双曲线x2－y2=1的左、右焦点，P为双曲线左支上任一点，过点F1作∠F1PF2的平分线的垂线，垂足为H，则|OH|=(　　)

A．1            B．2          C．4            D．0.5

10.已知双曲线C：－=1(a＞0，b＞0)的焦距为2c，直线l过点且与双曲线C的一条渐近线垂直，以双曲线C的右焦点为圆心，半焦距为半径的圆Ω与直线l交于M，N两点，若|MN|=c，则双曲线C的渐近线方程为(　　)

A．y=±x          B．y=±x         C．y=±2x            D．y=±4x

11.过双曲线－=1(a＞0，b＞0)的右焦点且垂直于x轴的直线与双曲线交于A，B两点，与双曲线的渐近线交于C，D两点，若|AB|≥|CD|，则双曲线离心率的取值范围为(　　)

A.       B.       C.        D.

12.已知双曲线(a＞0，b＞0)的两条渐近线均与曲线C：x2＋y2-6x＋5=0相切，则该双曲线的离心率等于(　　)

A.         B.         C.          D.

二 、填空题

13.双曲线－=1的离心率为.则m=________.

14.设点P是双曲线-=1上任意一点，F1，F2分别是其左、右焦点，若|PF1|=10，则|PF2|=________.

15.若双曲线－=1(a>0，b>0)的两个焦点分别为F1、F2，P为双曲线上一点，且|PF1|=3|PF2|，则该双曲线离心率e的取值范围是________.

16.设P为双曲线x2－=1上的一点，F1，F2是该双曲线的左、右焦点，若△PF1F2的面积为12，

则∠F1PF2=________．

三 、解答题

17.设F1，F2为双曲线－y2=1的两个焦点，点P在双曲线上，且满足∠F1PF2=120°.求△F1PF2的面积.

18.求适合下列条件的双曲线的标准方程：

(1)以椭圆＋=1的长轴端点为焦点，且经过点P(5，)；

(2)过点P1(3，－4 )，P2(，5).

19.已知点F1，F2分别是双曲线C：x2－=1(b＞0)的左、右焦点，过F2作垂直于x轴的直线，在x轴上方交双曲线C于点M，∠MF1F2=30°.

(1)求双曲线C的方程；

(2)过双曲线C上任意一点P作该双曲线两条渐近线的垂线，垂足分别为P1，P2，求·的值．

20.已知双曲线C：-=1(a>0，b>0)的一条渐近线的方程为y=x，右焦点F到直线x=的距离为．

(1)求双曲线C的方程；

(2)斜率为1且在y轴上的截距大于0的直线l与双曲线C相交于B，D两点，已知A(1，0)，若·=1，证明：过A，B，D三点的圆与x轴相切．

参考答案

1.答案为：D；

2.答案为：A；

解析：∵e==，∴==e2-1=3-1=2，∴=．

因为该双曲线的渐近线方程为y=±x，所以该双曲线的渐近线方程为y=±x，故选A．

3.答案为：C；

解析：由双曲线－=1(a＞0，b＞0)的渐近线方程为y=±x，

且双曲线的一条渐近线方程为y=－2x，得=2，则b=2a，

则双曲线的离心率e=====.故选C.

4.答案为：A；

解析：∵-=1的焦距为10，∴c=5=．①

又双曲线渐近线方程为y=±x，且P(2，1)在渐近线上，∴=1，即a=2b．②

由①②解得a=2，b=，则C的方程为-=1．故选A．

5.答案为：D；

6.B.

7.答案为：D；

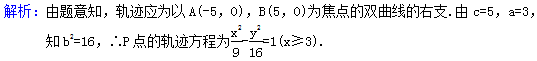
解析：

如图，设左焦点为F′，连接MF′，NF′，令|MF|=r1，|MF′|=r2，则|NF|=|MF′|=r2，

由双曲线定义可知r2-r1=2a　①，∵点M与点N关于原点对称，且MF⊥NF，

∴|OM|=|ON|=|OF|=c，∴r＋r=4c2　②，由①②得r1r2=2(c2-a2)，又知S△MNF=2S△MOF．

∴r1r2=2·c2·sin2β，∴c2-a2=c2·sin2β，∴e2=，

又∵β∈，，∴sin2β∈，，∴e2=∈[2，(＋1)2]．

又e>1，∴e∈[，＋1]，故选D．

8.答案为：D；

9.答案为：A；

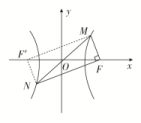
解析：如图，延长F1H交PF2于点Q，由PH为∠F1PF2的平分线及PH⊥F1Q，可知|PF1|=|PQ|，

根据双曲线的定义，得|PF2|－|PF1|=2，从而|QF2|=2，在△F1QF2中，易知OH为中位线，

故|OH|=1.故选A.

10.答案为：B.

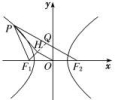
解析：由题意得，双曲线的渐近线方程为y=±x，设垂直于直线l的渐近线方程为y=x，

则直线l的斜率k1=－，直线l的方程为y=－，整理可得，ax＋by－a2=0，

焦点(c，0)到直线l的距离d==，

则|MN|=2=2=c，整理可得c4－9a2c2＋12a3c－4a4=0，

即e4－9e2＋12e－4=0，即(e－1)(e－2)(e2＋3e－2)=0，又双曲线的离心率e＞1，

所以e==2，所以b=a，故双曲线C的渐近线方程为y=±x，故选B.

11.答案为：B；

解析：将x=c代入－=1得y=±，不妨取A，B，所以|AB|=.

将x=c代入双曲线的渐近线方程y=±x，得y=±，

不妨取C，D，所以|CD|=.

因为|AB|≥|CD|，所以≥×，即b≥c，则b2≥c2，即c2－a2≥c2，

即c2≥a2，所以e2≥，所以e≥.

12.答案为：A；

二 、填空题

13.答案为：9

解析：∵a=4，b=，∴c2=16＋m，e===，∴m=9.

14.答案为：16或4；

解析：由双曲线的标准方程得a=3，b=4.于是c==5.

(1)若点P在双曲线的左支上，则|PF2|-|PF1|=2a=6，∴|PF2|=6＋|PF1|=16；

(2)若点P在双曲线的右支上，则|PF1|-|PF2|=6，∴|PF2|=|PF1|-6=10-6=4.

综上，|PF2|=16或4.

15.答案为：(1,2]

解析：依题意得由此解得|PF2|=a，|PF1|=3a，

∵|PF1|＋|PF2|≥|F1F2|，即c≤2a，e=≤2.又e>1，∴离心率e的取值范围是(1,2].

16.答案为：；

解析：由题意可知，F1(－，0)，F2(，0)，|F1F2|=2.设P(x0，y0)，

则△PF1F2的面积为×2|y0|=12.故y=，将P点坐标代入双曲线方程得x=，

不妨设点P，则=(，)，=，

可得·=0，即PF1⊥PF2，故∠F1PF2=.

三 、解答题

17.解：由已知得a=2，b=1；c= =，

由余弦定理得：F1F=PF＋PF－2PF1·PF2cos 120°

即(2 )2=(PF1－PF2)2＋3PF1·PF2

∵|PF1－PF2|=4.∴PF1·PF2=.

∴S△F1PF2=PF1·PF2·sin 120°=××=.

18.解：

(1)因为椭圆＋=1的长轴端点为A1(－5,0)，A2(5,0)，

所以所求双曲线的焦点为F1(－5,0)，F2(5,0).

由双曲线的定义知，|PF1－PF2|

===8，

即2a=8，则a=4.

又c=5，所以b2=c2－a2=9.

故所求双曲线的标准方程为－=1.

(2)设双曲线的方程为Ax2＋By2=1(AB<0)，分别将点P1(3，－4 )，P2(，5)代入，

得解得

故所求双曲线的标准方程为－=1.

19.解：

(1)由题易知F2(，0)，可设M(，y1)．

因为点M在双曲线C上且在x轴上方，所以1＋b2－=1，得y1=b2，所以|F2M|=b2.

在Rt△MF2F1中，∠MF1F2=30°，|MF2|=b2，所以|MF1|=2b2.由双曲线的定义可知，

|MF1|－|MF2|=b2=2，故双曲线C的方程为x2－=1.

(2)易知两条渐近线方程分别为l1：x－y=0，l2：x＋y=0.

设双曲线C上的点P(x0，y0)，两条渐近线的夹角为θ，

不妨设P1在l1上，P2在l2上，

则点P到两条渐近线的距离分别为|PP1|=，|PP2|=.

因为P(x0，y0)在双曲线x2－=1上，所以2x－y=2，

又易知cos θ=，所以·=·cos θ=·=.

20.解：

(1)依题意有=，c-=，

∵a2＋b2=c2，∴c=2a，∴a=1，c=2，∴b2=3，

∴双曲线C的方程为x2-=1．

(2)证明：设直线l的方程为y=x＋m(m>0)，B(x1，x1＋m)，D(x2，x2＋m)，BD的中点为M，

由得2x2-2mx-m2-3=0，∴x1＋x2=m，x1x2=-，

又∵·=1，即(2-x1)(2-x2)＋(x1＋m)(x2＋m)=1，∴m=0(舍)或m=2，

∴x1＋x2=2，x1x2=-，M点的横坐标为=1，

∵·=(1-x1)(1-x2)＋(x1＋2)(x2＋2)=5＋2x1x2＋x1＋x2=5-7＋2=0，

∴AD⊥AB，

∴过A，B，D三点的圆以点M为圆心，BD为直径，

∵点M的横坐标为1，∴MA⊥x轴，

∵|MA|=|BD|，

∴过A，B，D三点的圆与x轴相切．