高考数学一轮复习夯基练习：指数与指数函数(含答案)

这是一份高考数学一轮复习夯基练习：指数与指数函数(含答案)，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
夯基练习 指数与指数函数一 、选择题1.函数，使成立的的值的集合是（    ）A、     B、     C、     D、  2.当x>0时，函数f(x)=(a2-1)x的值总大于1，则实数a的取值范围是(　　)A．1<|a|<2      B．|a|<1       C．|a|>       D．|a|<  3.下列判断正确的是(　　)A.2.52.5>2.53     B.0.82<0.83            C.π2<π      D.0.90.3>0.90.5 4.函数y=ax+b(a>0且a≠1)与y=ax+b的图象有可能是(　   ) .5.如图是指数函数①y=ax，②y=bx，③y=cx，④y=dx的图象，则a、b、c、d与1的大小关系是(　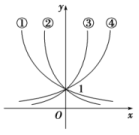　)A.a＜b＜1＜c＜d         B.b＜a＜1＜d＜cC.1＜a＜b＜c＜d         D.a＜b＜1＜d＜c 6.已知函数f(x)=ax，其中a＞0，且a≠1，如果以P(x1，f(x1))，Q(x2，f(x2))为端点的线段的中点在y轴上，那么f(x1)·f(x2)等于(　　)A．1           B．a            C．2           D．a2  7.函数y=2x-1的值域是（   ）A、R    B、（-∞，0）    C、（-∞，-1）    D、（-1，+∞） 8.设<()b<()a<1，那么(　　)A.aa<ab<ba         B.aa<ba<ab           C.ab<aa<ba         D.ab<ba<aa  9.下列一定是指数函数的是(　　)A.形如y=ax的函数B.y=xa(a＞0，且a≠1)C.y=(|a|＋2)-xD.y=(a-2)ax  10.下列函数中，指数函数的个数为(　　)①y=(0.5)x－1；②y=ax(a>0，且a≠1)；③y=1x；④y=(0.5)2x－1.A.0个          B.1个　       C.3个          D.4个  11.函数y=2－x＋1＋2的图象可以由函数y=(0.5)x的图象经过怎样的平移得到(　　)A.先向左平移1个单位，再向上平移2个单位B.先向左平移1个单位，再向下平移2个单位C.先向右平移1个单位，再向上平移2个单位D.先向右平移1个单位，再向下平移2个单位  12.设函数f(x)定义在实数集上，它的图象关于直线x=1对称，且当x≥1时，f(x)=3x－1，则有(       )  二 、填空题13.已知y=21＋ax在R上是减函数，则a的取值范围是________. 14.函数f(x)=的单调增区间为            ，值域为               .15.若函数f(x)=ax(a>0,且a≠1)在[-1,2]上的最大值为4,最小值为m,且函数g(x)=(1-4m)在[0,+∞)上是增函数,则a=　　　　.  16.若函数f(x)= 的定义域为R，则a的取值范围是________.  三 、解答题17.已知x+x-1=3，求x2+x-2的值。  18.已知函数(a＞1).（1）判断函数f (x)的奇偶性；（2）求f (x)的值域；（3）证明f (x)在(－∞，+∞)上是增函数.         19.已知定义域为R的函数f(x)=是奇函数.(1)求实数a的值；(2)用定义证明：f(x)在R上是减函数.          20.计算：(n>1，且n∈N*)；
参考答案1.C；2.答案为：C；解析：∵x>0时，f(x)=(a2-1)x的值总大于1，∴a2-1>1，即a2>2．∴|a|>．故选C．  3.答案为：D；解析：函数y=0.9x在R上为减函数，所以0.90.3>0.90.5.4.答案为：D5.答案为：B；解析：法一：当指数函数底数大于1时，图象上升，且当底数越大，图象向上越靠近于y轴；当底数大于0小于1时，图象下降，底数越小，图象向右越靠近于x轴，得b＜a＜1＜d＜c.法二　令x=1，由题图知c1＞d1＞a1＞b1，∴b＜a＜1＜d＜c. 6.答案为：A；解析：选A.∵以P(x1，f(x1))，Q(x2，f(x2))为端点的线段的中点在y轴上，∴x1＋x2=0.又∵f(x)=ax，∴f(x1)·f(x2)=ax1·ax2=ax1＋x2=a0=1，故选A.  7.D8.答案为：C；解析：由已知及函数y=()x是R上的减函数，得0<a<b<1.由y=ax(0<a<1)的单调性及a<b，得ab<aa.由0<a<b<1知0<<1.∵()a<()0=1.∴aa<ba.故选C.也可采用特殊值法，如果a=，b=.  9.答案为：C；  10.答案为：B;解析：由指数函数的定义可判定，只有②正确.  11.答案为：C；解析：y=2－x＋1＋2=(0.5)x－1＋2，设f(x)=(0.5)x，则f(x－1)＋2=(0.5)x－1＋2，要想得到y=2－x＋1＋2的图象，只需将y=(0.5)x图象先向右平移1个单位，再向上平移2个单位.  12.B.因为f(x)的图象关于直线x=1对称，所以f(1/3)=f(5/3)，f(2/3)=f(4/3)，因为函数f(x)=3x－1在[1，＋∞)上是增函数，所以f(5/3)>f(3/2)>f(4/3)，即f(2/3)<f(3/2)<f(1/3)．故选B. 二 、填空题13.答案为：(－∞，0)；解析：∵y=21＋ax=2×2ax在R上是减函数，∴a<0，即a的取值范围是(－∞，0). 14.答案为：(-∞，1]，(0,3]；15.答案　解析　g(x)=(1-4m)在[0,+∞)上是增函数,应有1-4m>0,即m<.当a>1时, f(x)=ax为增函数,由题意知⇒m=,与m<矛盾.当0<a<1时, f(x)=ax为减函数,由题意知⇒m=,满足m<.故a=. 16.答案为：[－1,0]；解析：∵f(x)的定义域为R，∴2 x2＋2ax－a－1≥0恒成立，即x2＋2ax－a≥0恒成立.∴Δ=4a2＋4a≤0，－1≤a≤0.  三 、解答题17.718.解：(1)是奇函数.(2)值域为(－1，1).(3)设x1＜x2，则。=∵a＞1，x1＜x2，∴a＜a.  又∵a+1＞0，a+1＞0，∴f (x1)－f (x2)＜0，即f (x1)＜f (x2).函数f(x)在(－∞，+∞)上是增函数.19.解：(1)因为f(x)是奇函数，所以f(－x)=－f(x)，令x=0，则f(0)=0，即=0⇒a=1，所以f(x)=.(2)证明：由(1)知f(x)==－1＋，任取x1，x2∈R，且x1<x2，则f(x2)－f(x1)=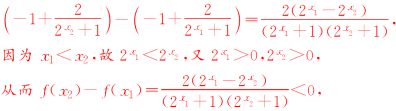即f(x1)>f(x2)，故f(x)在R上是减函数.  20.当x≥y时，原式=x-y；当x<y时，原式=y-x.