高考数学二轮复习题海集训08 空间几何体（30题含答案）

这是一份高考数学二轮复习题海集训08 空间几何体（30题含答案），共10页。
2020高考数学(理数)题海集训08 空间几何体一         、选择题1.将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体是由(　　)A.一个圆台、两个圆锥构成         B.两个圆台、一个圆锥构成C.两个圆柱、一个圆锥构成         D.一个圆柱、两个圆锥构成 2.下列说法中正确的是(　　)A．各个面都是三角形的几何体是三棱锥B．以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥C．棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是六棱锥D．圆锥的顶点与底面圆周上的任一点的连线都是母线  3.若三个球的表面积之比为1:2:3，则它们的体积之比为(　　)A.1:2:3             B.1::      C.1:2:3        D.1:4:7 4.在长方体ABCD­A1B1C1D1中，AB=BC=2，AC1与平面BB1C1C所成的角为30°，则该长方体的体积为(　　)A．8           B．6            C．8           D．8  5.已知在长方体ABCD­A1B1C1D1中，底面是边长为2的正方形，高为4，则点A1到截面AB1D1的距离是(　　)A.           B．           C.           D．6.如图，在四边形ABCD中，∠DAB=90°，∠ADC=135°，AB=5，CD=2，AD=2，则四边形ABCD绕AD旋转一周所成几何体的表面积为(  )                                          A.(60+4)π   B.(60+8)π     C.(56+8)π      D.(56+4)π 7.下列几何体各自的三视图中，有且仅有两个视图相同的是(　　)A．①②　　         B．①③        C．①④             D．②④8.如图，在透明塑料制成的长方体ABCD﹣A1B1C1D1容器内灌进一些水，将容器底面一边BC固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个说法：                            ①水的部分始终呈棱柱状；              ②水面四边形EFGH的面积不改变；              ③棱A1D1始终与水面EFGH平行；              ④当E∈AA1时，AE+BF是定值.其中正确说法的是(  )                                          A.②③④        B.①②④        C.①③④                      D.①②③9.正方体的内切球和外接球的体积之比为(　　)A.1:               B.1:3        C.1:3              D.1:9 10.某正三棱锥正视图如图所示，则俯视图的面积为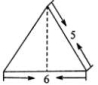（   ）A.            B.        C.         D. 11.已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点，若三棱锥O­ABC体积的最大值为36，则球O的表面积为(　　)A．36π            B．64π         C．144π           D．256π 12.一个几何体的三视图如上图所示，则该几何体的体积为（  ）   A.    B.    C.    D.  13.水平放置的△ABC的直观图如图，其中B′O′=C′O′=1，A′O′=，那么原△ABC是一个（　　）A.等边三角形                              B.直角三角形   C.三边中只有两边相等的等腰三角形          D.三边互不相等的三角形14.平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为(　　)A.π          B．4π         C．4π        D．6π  15.如图所示，等腰△A′B′C′是△ABC的直观图，那么△ABC是(　　)A．等腰三角形        B．直角三角形     C．等腰直角三角形      D．钝角三角形 16.一个长方体去掉一个小长方体，所得几何体的正视图与侧视图分别如图所示，则该几何体的俯视图为(　　) 17.一空间几何体的三视图如图所示，则该几何体的体积为(　　)A.         B.     C.          D. 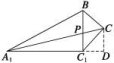18.已知四面体P­ABC的四个顶点都在球O的球面上，PA=8，BC=4，PB=PC=AB=AC，且平面PBC⊥平面ABC，则球O的表面积为(　　)A．64π            B．65π           C．66π            D．128π 19.若三棱锥S­ABC的所有顶点都在球O的球面上，SA⊥平面ABC，SA=2，AB=1，AC=2，∠BAC=60°，则球O的表面积为(　　)A．64π            B．63π          C．65π            D．32π 20.一个四棱锥的侧棱长都相等，底面是正方形，其正(主)视图如图所示，则该四棱锥的侧面积和体积分别是(　　)A．4，8            B．4，         C．4(＋1)，          D．8，8 二         、填空题21.已知圆锥侧面展开图的圆心角为90°，则该圆锥的底面半径与母线长的比为________． 22.如图所示，在直三棱柱ABC－A1B1C1中，底面为直角三角形，∠ACB=90°，AC=6，BC=CC1=，P是BC1上一动点，则CP＋PA1的最小值是___________.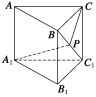 23.如图，直角梯形ABCD中，AD⊥DC，AD∥BC，BC=2CD=2AD=2，若将该直角梯形绕BC边旋转一周，则所得的几何体的表面积为________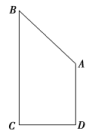． 24.已知三棱锥S-ABC的所有顶点都在球O的球面上，SC是球O的直径。若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S-ABC的体积为9，则球O的表面积为________。 25.已知底面是正六边形的六棱锥P­ABCDEF的七个顶点均在球O的表面上，底面正六边形的边长为1，若该六棱锥体积的最大值为，则球O的表面积为________．    26.如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________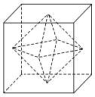． 27.如图直三棱柱ABC­A1B1C1的六个顶点都在半径为1的半球面上，AB=AC，侧面BCC1B1是半球底面圆的内接正方形，则侧面ABB1A1的面积为________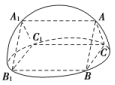． 28.如图，在正三棱柱ABC-A1B1C1中，已知AB=AA1=3，点P在棱CC1上，则三棱锥P-ABA1的体积为  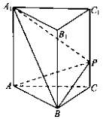        . 29.已知圆锥的顶点为S，母线SA，SB所成角的余弦值为，SA与圆锥底面所成角为45°，若△SAB的面积为5，则该圆锥的侧面积为________．  30.鲁班锁是中国传统的智力玩具，起源于中国古代建筑中首创的榫卯结构，它的外观是如图所示的十字立方体，其上下、左右、前后完全对称，六根等长的正四棱柱分成三组，经90°榫卯起来．若正四棱柱的高为5，底面正方形的边长为1，现将该鲁班锁放进一个球形容器内，则该球形容器的表面积至少为________．(容器壁的厚度忽略不计，结果保留π)  
答案解析1.答案为：D；　2.答案为：D；解析：当一个几何体由具有相同的底面且顶点在底面两侧的两个三棱锥构成时，尽管各面都是三角形，但它不是三棱锥，故A错误；若三角形不是直角三角形或是直角三角形但旋转轴不是直角边所在直线，所得几何体就不是圆锥，故B错误；若六棱锥的所有棱都相等，则底面多边形是正六边形，由几何图形知，若以正六边形为底面，则棱长必然要大于底面边长，故C错误．选D.  3.答案为：C;解析：由表面积之比得到半径之比为r1:r2:r3=1::，从而得体积之比为V1:V2:V3=1:2:3.4.答案为：C；解析：如图，连接AC1，BC1，AC.∵AB⊥平面BB1C1C，∴∠AC1B为直线AC1与平面BB1C1C所成的角，∴∠AC1B=30°.又AB=BC=2，在Rt△ABC1中，AC1==4.在Rt△ACC1中，CC1===2，∴V长方体=AB×BC×CC1=2×2×2=8.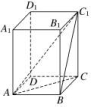  5.答案为：C.解析：设点A1到截面AB1D1的距离是h，由VA1­AB1D1=VA­A1B1D1，可得S△AB1D1·h=S△A1B1D1·AA1，即××2×2×4=×h，解得h=.6.A.解析：四边形ABCD绕AD旋转一周所成的几何体，如图：                                          S表面=S圆台下底面+S圆台侧面+S圆锥侧面=πr22+π(r1+r2)l2+πr1l1=(60+4)π，                                                                                      7.答案为：D.解析：①中正、侧、俯三视图均相同，不符合题意；②中正、侧视图均相同，符合题意；③中正、侧、俯三视图均不相同，不符合题意；④中正、侧视图均相同，符合题意．   8.C.                                          解析：①水的部分始终呈棱柱状；从棱柱的特征平面AA1B1B平行平面CC1D1D即可判断①正确；                                          ②水面四边形EFGH的面积不改变；EF是可以变化的EH不变的，所以面积是改变的，②是不正确的；              ③棱A1D1始终与水面EFGH平行；由直线与平面平行的判断定理，可知A1D1∥EH，所以结论正确；④当E∈AA1时，AE+BF是定值.水的体积是定值，高不变，所以底面面积不变，所以正确.                            9.答案为：C；解析：关键要清楚正方体内切球的直径等于棱长a，外接球的直径等于a.10.D；解析：由正视图知，该正三棱锥的底边长为6，高为4，则侧视图是一个底边长为，高为的三角形，其面积为.11.答案为：C.解析：如图所示，当点C位于垂直于面AOB的直径端点时，三棱锥O­ABC的体积最大，设球O的半径为R，此时VO­ABC=VC­AOB=×R2×R=R3=36，故R=6，则球O的表面积为S=4πR2=144π.12.答案为：B； 13.A.14.答案为：B；解析：设球的半径为R，由球的截面性质得R==，所以球的体积V=πR3=4π. 15.答案为：B；解析：由题图知A′C′∥y′轴，A′B′∥x′轴，由斜二测画法知，在△ABC中，AC∥y轴，AB∥x轴，∴AC⊥AB.又因为A′C′=A′B′，∴AC=2AB≠AB，∴△ABC是直角三角形． 16.答案为：C；解析：由三视图中的正、侧视图得到几何体的直观图如图所示，所以该几何体的俯视图为C.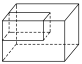  17.答案为：C； 18.答案为：B.解析：如图，D，E分别为BC，PA的中点，易知球心O在线段DE上．∵PB=PC=AB=AC，∴PD⊥BC，AD⊥BC，PD=AD.又平面PBC⊥平面ABC，平面PBC∩平面ABC=BC，∴PD⊥平面ABC.∴PD⊥AD.∴PD=AD=4.∵点E是PA的中点，∴ED⊥PA，且DE=EA=PE=4.设球O的半径为R，OE=x，则OD=4－x.在Rt△OEA中，有R2=16＋x2，在Rt△OBD中，有R2=4＋(4－x)2，解得R2=，所以S=4πR2=65π，故选B.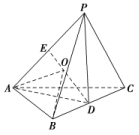 19.答案为：A.解析：设球O的半径为R，∵AB=1，AC=2，∠BAC=60°，∴BC2=1＋4－2×1×2×cos 60°=3，所以AB2＋BC2=AC2.即△ABC为直角三角形，那么△ABC所在截面圆的直径为AC，所以(2R)2=SA2＋AC2=64.所以S球=4πR2=64π.  20.答案为：B.解析：由正视图知：四棱锥的底面是边长为2的正方形，四棱锥的高为2，∴四棱锥的体积V=×22×2=；四棱锥的侧面是全等的等腰三角形，底为2，高为，∴S侧=4××2×=4.21.答案为：；解析：设圆锥的母线长是R，则扇形的弧长是=，设底面半径是r，则=2πr，所以r=，所以圆锥的底面半径与母线长的比为1∶4.     22.答案为：； 23.答案为：(＋3)π；解析：根据题意可知，该几何体的上半部分为圆锥(底面半径为1，高为1)，下半部分为圆柱(底面半径为1，高为1)，如图所示，则所得几何体的表面积为圆锥侧面积、圆柱的侧面积以及圆柱的下底面面积之和，即表面积为π×1×＋2π×12＋π×12=(＋3)π. 24.【答案】   25.答案为：；解析：因为六棱锥P­ABCDEF的七个顶点均在球O的表面上，由对称性和底面正六边形的面积为定值知，当六棱锥P­ABCDEF为正六棱锥时，体积最大．设正六棱锥的高为h，则×h=，解得h=2.记球O的半径为R，根据平面截球面的性质，得(2－R)2＋12=R2，解得R=，所以球O的表面积为4πR2=4π=. 26.答案为：；解析：由题意知所给的几何体是棱长均为的八面体，它是由两个有公共底面的正四棱锥组合而成的，正四棱锥的高为1，所以这个八面体的体积为2V正四棱锥=2××()2×1=.  27.答案为：；解析：由题意知，球心在侧面BCC1B1的中心O上，BC为截面圆的直径，所以∠BAC=90°，△ABC的外接圆圆心N是BC的中点，同理△A1B1C1的外心M是B1C1的中点．△设正方形BCC1B1的边长为x.在Rt△OMC1中，OM=，MC1=，OC1=R=1(R为球的半径)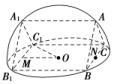，所以＋=1，即x=，则AB=AC=1，所以S矩形ABB1A1=×1=. 28.答案为：；解析：  29.答案为：40π；解析：如图，∵SA与底面成45°角，∴△SAO为等腰直角三角形．设OA=r，则SO=r，SA=SB=r.在△SAB中，cos∠ASB=，∴sin∠ASB=，∴S△SAB=SA·SB·sin∠ASB=×(r)2×=5，解得r=2，∴SA=r=4，即母线长l=4，∴S圆锥侧=πrl=π×2×4=40π.  30.答案为：30π；解析：该球形容器最小时，两个正四棱柱组成的四棱柱与球内接，此时球的直径2R等于四棱柱的体对角线，即2R==，故球形容器的表面积为4πR2=30π.