


所属成套资源:高考数学二轮复习题海集训 (30题含答案)
高考数学二轮复习题海集训13 统计(30题含答案)
展开
这是一份高考数学二轮复习题海集训13 统计(30题含答案),共10页。
2020高考数学(理数)题海集训13 统计 一 、选择题1.对一个容量为N的总体抽取容量为n的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为p1,p2,p3,则( )A.p1=p2<p3 B.p2=p3<p1 C.p1=p3<p2 D.p1=p2=p3 2.某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )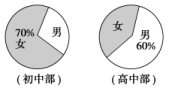 A.93 B.123 C.137 D.167 3.现用系统抽样方法从已编号(1~60)的60枚新型导弹中,随机抽取6枚进行试验,则所选取的6枚导弹的编号可能是( )A.5,10,15,20,25,30 B.2,4,8,16,32,48C.5,15,25,35,45,55 D.1,12,34,47,51,60 4.某班有34位同学,座位号记为01,02,…,34,用下面的随机数表选取5组数作为参加青年志愿者活动的五位同学的座号.选取方法是从随机数表第一行的第6列数字开始,由左到右依次选取两个数字,则选出来的第4个志愿者的座号是( )
A.93 B.123 C.137 D.167 3.现用系统抽样方法从已编号(1~60)的60枚新型导弹中,随机抽取6枚进行试验,则所选取的6枚导弹的编号可能是( )A.5,10,15,20,25,30 B.2,4,8,16,32,48C.5,15,25,35,45,55 D.1,12,34,47,51,60 4.某班有34位同学,座位号记为01,02,…,34,用下面的随机数表选取5组数作为参加青年志愿者活动的五位同学的座号.选取方法是从随机数表第一行的第6列数字开始,由左到右依次选取两个数字,则选出来的第4个志愿者的座号是( ) A.23 B.09 C.02 D.16 5.某工厂的一、二、三车间在2017年11月份共生产了3 600双皮靴,在出厂前检查这批产品的质量,决定采用分层抽样的方法进行抽取,若从一、二、三车间抽取的产品数分别为a、b、c,且a、b、c成等差数列,则二车间生产的产品数为( )A.800 B.1 000 C.1 200 D.1 500 6.某班对八校联考成绩进行分析,利用随机数表法抽取样本时,先将60个同学的成绩按01,02,03,…,60进行编号,然后从随机数表第9行第5列的数开始向右读,则选出的第6个个体是(注:下表为随机数表的第8行和第9行)( )
A.23 B.09 C.02 D.16 5.某工厂的一、二、三车间在2017年11月份共生产了3 600双皮靴,在出厂前检查这批产品的质量,决定采用分层抽样的方法进行抽取,若从一、二、三车间抽取的产品数分别为a、b、c,且a、b、c成等差数列,则二车间生产的产品数为( )A.800 B.1 000 C.1 200 D.1 500 6.某班对八校联考成绩进行分析,利用随机数表法抽取样本时,先将60个同学的成绩按01,02,03,…,60进行编号,然后从随机数表第9行第5列的数开始向右读,则选出的第6个个体是(注:下表为随机数表的第8行和第9行)( ) A.07 B.25 C.42 D.52 7.某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为42的样本,则应分别抽取老年人、中年人、青年人的人数是( )A.7,11,18 B.6,12,18 C.6,13,17 D.7,14,21 8.已知某班级部分同学一次测验的成绩统计如下茎叶图所示,则其中位数和众数分别为( )
A.07 B.25 C.42 D.52 7.某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为42的样本,则应分别抽取老年人、中年人、青年人的人数是( )A.7,11,18 B.6,12,18 C.6,13,17 D.7,14,21 8.已知某班级部分同学一次测验的成绩统计如下茎叶图所示,则其中位数和众数分别为( ) A.95,94 B.92,86 C.99,86 D.95,91 9.在如图所示一组数据的茎叶图中,有一个数字被污染后模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )
A.95,94 B.92,86 C.99,86 D.95,91 9.在如图所示一组数据的茎叶图中,有一个数字被污染后模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )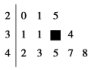 A.1 B.2 C.3 D.4 10.某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示,以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )
A.1 B.2 C.3 D.4 10.某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示,以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )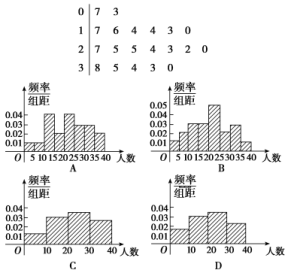 11.如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
11.如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )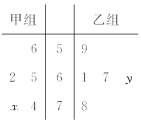 A.3,5 B.5,5 C.3,7 D.5,7 12.生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85 mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
A.3,5 B.5,5 C.3,7 D.5,7 12.生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85 mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )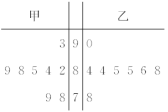 A.甲、乙生产的零件尺寸的中位数相等B.甲、乙生产的零件质量相当C.甲生产的零件质量比乙生产的零件质量好D.乙生产的零件质量比甲生产的零件质量好 13.为了解学生“阳光体育”活动的情况,随机统计了n名学生的“阳光体育”活动时间(单位:分钟),所得数据都在区间[10,110]内,其频率分布直方图如图所示.已知活动时间在[10,35)内的频数为80,则n的值为( )
A.甲、乙生产的零件尺寸的中位数相等B.甲、乙生产的零件质量相当C.甲生产的零件质量比乙生产的零件质量好D.乙生产的零件质量比甲生产的零件质量好 13.为了解学生“阳光体育”活动的情况,随机统计了n名学生的“阳光体育”活动时间(单位:分钟),所得数据都在区间[10,110]内,其频率分布直方图如图所示.已知活动时间在[10,35)内的频数为80,则n的值为( )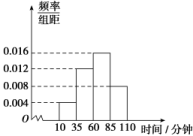 A.700 B.800 C.850 D.900 14.为了了解某市市民对共享单车布点的满意程度,从该市市民中随机抽查若干人,按年龄(单位:岁)分组,得到样本的频率分布直方图如图,其中年龄在[30,40)内的有500人,年龄在[20,30)内的有200人,则m的值为( )
A.700 B.800 C.850 D.900 14.为了了解某市市民对共享单车布点的满意程度,从该市市民中随机抽查若干人,按年龄(单位:岁)分组,得到样本的频率分布直方图如图,其中年龄在[30,40)内的有500人,年龄在[20,30)内的有200人,则m的值为( )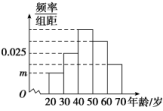 A.0.012 B.0.011 C.0.010 D.0.009 15.把样本容量为20的数据分组,分组区间与频数如下:[10,20),2;[20,30),3;[30,40),4;[40,50),5;[50,60),4;[60,70],2,则在区间[10,50)上的数据的频率是( )A.0.05 B.0.25 C.0.5 D.0.7 16.某商场在国庆黄金周的促销活动中,对10月2日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时到12时的销售额为( )
A.0.012 B.0.011 C.0.010 D.0.009 15.把样本容量为20的数据分组,分组区间与频数如下:[10,20),2;[20,30),3;[30,40),4;[40,50),5;[50,60),4;[60,70],2,则在区间[10,50)上的数据的频率是( )A.0.05 B.0.25 C.0.5 D.0.7 16.某商场在国庆黄金周的促销活动中,对10月2日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时到12时的销售额为( )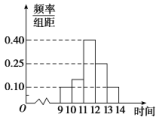 A.6万元 B.8万元 C.10万元 D.12万元 17.一个样本a,3,5,7的平均数是b,且a,b分别是数列{2n-2}(n∈N*)的第2项和第4项,则这个样本的方差是( )A.3 B.4 C.5 D.6 18.检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5~105.5之间的产品数为150,则质量在115.5~120.5的长方形高度为( )
A.6万元 B.8万元 C.10万元 D.12万元 17.一个样本a,3,5,7的平均数是b,且a,b分别是数列{2n-2}(n∈N*)的第2项和第4项,则这个样本的方差是( )A.3 B.4 C.5 D.6 18.检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5~105.5之间的产品数为150,则质量在115.5~120.5的长方形高度为( )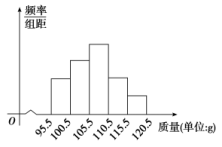 A. B. C. D. 19.下面四个残差图中可以反映出回归模型拟合精度较高的为( )
A. B. C. D. 19.下面四个残差图中可以反映出回归模型拟合精度较高的为( )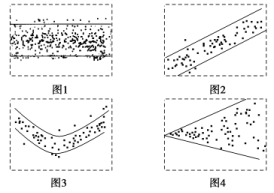 A.图1 B.图2 C.图3 D.图4 20.在样本频率分布直方图中,共有9个小长方形,若中间一个小长方形的面积等于其他8个小长方形的面积和的0.4,且样本容量为140,则中间一组的频数为( )A.28 B.40 C.56 D.60 二 、填空题21.有甲、乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计后,得到如下的列联表:
A.图1 B.图2 C.图3 D.图4 20.在样本频率分布直方图中,共有9个小长方形,若中间一个小长方形的面积等于其他8个小长方形的面积和的0.4,且样本容量为140,则中间一组的频数为( )A.28 B.40 C.56 D.60 二 、填空题21.有甲、乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计后,得到如下的列联表: 利用列联表的独立性检验估计,则成绩与班级________.(填“有关”或“无关”) 22.某学校为了调查学生在学科教辅书方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出的钱数在[30,40)的同学比支出的钱数在[10,20)的同学多26人,则n的值为________.
利用列联表的独立性检验估计,则成绩与班级________.(填“有关”或“无关”) 22.某学校为了调查学生在学科教辅书方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出的钱数在[30,40)的同学比支出的钱数在[10,20)的同学多26人,则n的值为________.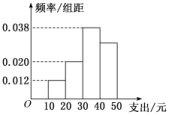 23.为了普及环保知识,增强环保意识,某大学有300名员工参加环保知识测试,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.现在要从第1,3,4组中用分层抽样的方法抽取16人,则在第4组中抽取的人数为________.
23.为了普及环保知识,增强环保意识,某大学有300名员工参加环保知识测试,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.现在要从第1,3,4组中用分层抽样的方法抽取16人,则在第4组中抽取的人数为________. 24.某学校高一、高二、高三年级的学生人数之比为4∶3∶3,现用分层抽样的方法从该校高中三个年级的学生中抽取一个容量为80的样本,则应从高一年级抽取________名学生. 25.一汽车制造厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
24.某学校高一、高二、高三年级的学生人数之比为4∶3∶3,现用分层抽样的方法从该校高中三个年级的学生中抽取一个容量为80的样本,则应从高一年级抽取________名学生. 25.一汽车制造厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆): 按类型用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆,则z的值为________. 26.某高校有教授120人,副教授100人,讲师80人,助教60人,现用分层抽样的方法从以上所有老师中抽取一个容量为n的样本.已知从讲师中抽取的人数为16,那么n=________. 27.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则x2+y2=________. 28.某棉纺厂为了解一批棉花的质量,从中随机抽测了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,则在抽测的100根中,有________根棉花纤维的长度小于20mm.
按类型用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆,则z的值为________. 26.某高校有教授120人,副教授100人,讲师80人,助教60人,现用分层抽样的方法从以上所有老师中抽取一个容量为n的样本.已知从讲师中抽取的人数为16,那么n=________. 27.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则x2+y2=________. 28.某棉纺厂为了解一批棉花的质量,从中随机抽测了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,则在抽测的100根中,有________根棉花纤维的长度小于20mm.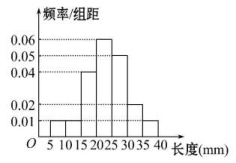 29.下方茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为14,乙组数据的平均数为16,则x+y的值为__________.
29.下方茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为14,乙组数据的平均数为16,则x+y的值为__________.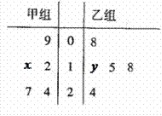 30.从某小学随机抽取100名同学,将他们的身高(单位
30.从某小学随机抽取100名同学,将他们的身高(单位![]() :厘米)数据绘制成频率分布直方图(如右图).由图中数据可知a=________.若要从身高在[ 120 , 130),[130 ,140), [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为________.
:厘米)数据绘制成频率分布直方图(如右图).由图中数据可知a=________.若要从身高在[ 120 , 130),[130 ,140), [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为________.
答案解析1.答案为:D.解析:由于三种抽样过程中,每个个体被抽到的概率都是相等的,因此p1=p2=p3. 2.答案为:C.解析:初中部的女教师人数为110×70%=77,高中部的女教师人数为150×(1-60%)=60,该校女教师的人数为77+60=137,故选C. 3.答案为:C.解析:从60枚新型导弹中随机抽取6枚,采用系统抽样间隔应为=10,只有C选项中导弹的编号间隔为10. 4.答案为:D.解析:从随机数表第一行的第6列数字3开始,由左到右依次选取两个数字,不超过34的依次为21,32,09,16,17,故第4个志愿者的座号为16. 5.答案为:C.解析:因为a、b、c成等差数列,所以2b=a+c,所以从二车间抽取的产品数占抽取产品总数的,根据分层抽样的性质可知,二车间生产的产品数占产品总数的,所以二车间生产的产品数为3 600×=1 200.故选C. 6.答案为:D.解析:依题意得,依次选出的个体分别是12,34,29,56,07,52,…,因此选出的第6个个体是52,选D. 7.答案为:D.因为该单位共有27+54+81=162(人),样本容量为42,所以应当按=的比例分别从老年人、中年人、青年人中抽取样本,且应分别抽取的人数是7,14,21.故选D. 8.答案为:B.解析:由茎叶图可知,此组数据由小到大排列依次为76,79,81,83,86,86,87,91,92,94,95,96,98,99,101,103,114,共17个,故中位数为92,出现次数最多的为众数,故众数为86,故选B. 9.答案为:B.解析:由题图可知该组数据的极差为48-20=28,则该组数据的中位数为61-28=33,设模糊数字为x,由=33,易得被污染的数字为2. 10.答案为:A.解析:由分组可知C,D一定不对;由茎叶图可知[0,5)有1人,[5,10)有1人,所以第一、二小组频率相同,频率分布直方图中矩形的高应相等,可排除B. 11.答案为:A.解析:由题意,甲组数据为56,62,65,70+x,74,乙组数据为59,61,67,60+y,78,要使两组数据中位数相等,有65=60+y,所以y=5,又平均数相同,则=,解得x=3. 12.答案为:D.解析:甲的零件尺寸是:93,89,88,85,84,82,79,78;乙的零件尺寸是:90,88,86,85,85,84,84,78;故甲的中位数是:=84.5,乙的中位数是:=85;故A错误;根据数据分析,乙的数据稳定,故乙生产的零件质量比甲生产的零件质量好,故B,C错误. 13.答案为:B.解析:根据频率分布直方图,知组距为25,所以活动时间在[10,35)内的频率为0.1.因为活动时间在[10,35)内的频数为80,所以n==800. 14.答案为:C.解析:由题意,年龄在[30,40)内的频率为0.025×10=0.25,则抽查的市民共有=2 000人.因为年龄在[20,30)内的有200人,所以m==0.010. 15.答案为:D.解析:由题意知,在区间[10,50)上的数据的频数是2+3+4+5=14,故其频率为=0.7. 16.答案为:C.解析:设11时到12时的销售额为x万元,依题意有=,解得x=10. 17.答案为:C.解析:因为样本a,3,5,7的平均数是b,且a,b分别是数列{2n-2}(n∈N*)的第2项和第4项,所以a=22-2=1,b=24-2=4,所以s2=[(1-4)2+(3-4)2+(5-4)2+(7-4)2]=5. 18.答案为:D.解析:根据题意,质量在100.5~105.5之间的产品数为150,频率为=0.25;前三组的长方形的高度成等差数列,设公差为d,则根据频率和为1,得(0.25-d)+0.25+(0.25+d)+(0.25+d)+(0.25+d)=1,解得d=.所以质量在115.5~120.5的频率是×=,对应小长方形的高为÷5=. 19.答案为:A.解析:根据残差图显示的分布情况即可看出,图1显示的残差点比较均匀地落在水平的带状区域中,所以拟合精度较高,故选A. 20.答案为:B.解析:设中间一组的频数为x,因为中间一个小长方形的面积等于其他8个小长方形的面积和的0.4,所以其他8组的频数和为x,由x+x=140,解得x=40. 一 、填空题21.答案为:无关;解析:成绩与班级有无关系,就是看随机变量的值与临界值2.706的大小关系.由公式得K2的观测值K2=≈0.653<2.706,所以成绩与班级无关. 22.答案为:100;解析:由频率分布直方图可得支出的钱数在[30,40)的同学有0.038×10n=0.38n个,支出的钱数在[10,20)的同学有0.012×10n=0.12n个,又支出的钱数在[30,40)的同学比支出的钱数在[10,20)的同学多26人,所以0.38n-0.12n=0.26n=26,解得n=100. 23.答案为:6;解析:根据频率分布直方图得,第1,3,4组的频率之比为1∶4∶3,所以用分层抽样的方法抽取16人时,在第4组中应抽取的人数为16×=6. 24.答案为:32;解析:从高一年级抽取的学生人数为80×=32. 25.答案为:400;解析:设该厂这个月共生产轿车n辆,由题意得=,所以n=2 000,则z=2 000-100-300-150-450-600=400. 26.答案为:72;解析:依题意得,=,由此解得n=72. 27.答案为:208;解析:由平均数为10,得(x+y+10+11+9)×![]() =10,则x+y=20;又由于方差为2,则[(x-10)2+(y-10)2+(10-10)2+(11-10)2+(9-10)2]×
=10,则x+y=20;又由于方差为2,则[(x-10)2+(y-10)2+(10-10)2+(11-10)2+(9-10)2]×![]() =2,整理得x2+y2-20(x+y)=-192.则x2+y2=20(x+y)-192=20×20-192=208.28.答案为:30;解析:由题意知,棉花纤维的长度小于20mm的频率为(0.01+0.01+0.04)×5=0.3,故抽测的100根中,棉花纤维的长度小于20mm的有0.3×100=30(根).29.答案为:9;30.答案为:0.030,3;
=2,整理得x2+y2-20(x+y)=-192.则x2+y2=20(x+y)-192=20×20-192=208.28.答案为:30;解析:由题意知,棉花纤维的长度小于20mm的频率为(0.01+0.01+0.04)×5=0.3,故抽测的100根中,棉花纤维的长度小于20mm的有0.3×100=30(根).29.答案为:9;30.答案为:0.030,3;
相关试卷
这是一份高考数学二轮复习题海集训34 导数的计算(30题含答案),共6页。
这是一份高考数学二轮复习题海集训32 双曲线(30题含答案),共10页。试卷主要包含了故选C,由左焦点F,等内容,欢迎下载使用。
这是一份高考数学二轮复习题海集训31 椭圆(30题含答案),共9页。









