


所属成套资源:高考数学二轮复习题海集训 (30题含答案)
高考数学二轮复习题海集训18 三角函数图象性质(30题含答案)
展开
这是一份高考数学二轮复习题海集训18 三角函数图象性质(30题含答案),共8页。
2020高考数学(理数)题海集训18 三角函数图象性质 一 、选择题1.函数![]() 的定义域是( )A.{x|x≠
的定义域是( )A.{x|x≠![]() ,x∈R} B.{x|x≠-
,x∈R} B.{x|x≠-![]() ,x∈R}C.{x|x≠
,x∈R}C.{x|x≠![]() ,k∈Z,x∈R} D.{x|x≠
,k∈Z,x∈R} D.{x|x≠![]() ,k∈Z,x∈R}2.函数y=3cos(
,k∈Z,x∈R}2.函数y=3cos(![]() x-
x-![]() )的最小正周期是( )A.
)的最小正周期是( )A.![]() B.
B.![]() C.2π D.5π3.已知函数y=sin在[0,t]上至少取得2次最大值,则正整数t的最小值为( )A.6 B.7 C.8 D.9 4.下列关系式中正确的是( )A.
C.2π D.5π3.已知函数y=sin在[0,t]上至少取得2次最大值,则正整数t的最小值为( )A.6 B.7 C.8 D.9 4.下列关系式中正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.设函数
5.设函数![]() ,则下列结论错误的是 ( ) A.
,则下列结论错误的是 ( ) A.![]() 的一个周期为
的一个周期为![]() B.
B.![]() 的图像关于直线
的图像关于直线![]() 对称 C.
对称 C.![]() 的一个零点为
的一个零点为![]() D.
D.![]() 在
在![]() 单调递减6.定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是π,且当x∈时,f(x)=sin x,则f的值为( )A.- B. C. D.7.函数y=sinx2的图象是( )
单调递减6.定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是π,且当x∈时,f(x)=sin x,则f的值为( )A.- B. C. D.7.函数y=sinx2的图象是( )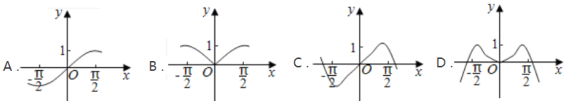 8.函数f(x)=sin在区间上的最小值为( )A.-1 B.- C. D.09.函数
8.函数f(x)=sin在区间上的最小值为( )A.-1 B.- C. D.09.函数![]() 的图象的一条对称轴方程为( )A.
的图象的一条对称轴方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.设ω>0,m>0,若函数f(x)=msin cos 在区间上单调递增,则ω的取值范围是( )A. B. C. D.[1,+∞)11.函数y=cosx(x∈R)的图象向左平移个单位后,得到函数y=g(x)的图象,则g(x)的解析式为( )A.-sinx B.sinx C.-cosx D.cosx12.若函数
10.设ω>0,m>0,若函数f(x)=msin cos 在区间上单调递增,则ω的取值范围是( )A. B. C. D.[1,+∞)11.函数y=cosx(x∈R)的图象向左平移个单位后,得到函数y=g(x)的图象,则g(x)的解析式为( )A.-sinx B.sinx C.-cosx D.cosx12.若函数![]() (x∈R),则f(x)( )A.在区间[
(x∈R),则f(x)( )A.在区间[![]() ]上是减函数 B.在区间[
]上是减函数 B.在区间[![]() ]上是增函数C.在区间[
]上是增函数C.在区间[![]() ]上是增函数 D.在区间[
]上是增函数 D.在区间[![]() ]上是减函数13.下列叙述:①作正弦函数的图象时,单位圆的半径长与x轴的单位长度必须一致;②y=sin x,x∈[0,2π]的图象关于点P(π,0)对称;③y=cos x,x∈[0,2π]的图象关于直线x=π成轴对称图形;④正、余弦函数y=sin x和y=cos x的图象不超出直线y=-1与y=1所夹的区域.其中正确的个数为( )A.1 B.2 C.3 D.414.若锐角φ满足sin φ-cos φ=,则函数f(x)=sin2(x+φ)的单调递增区间为( )A.(k∈Z) B.(k∈Z)C.(k∈Z) D.(k∈Z) 15.如果函数
]上是减函数13.下列叙述:①作正弦函数的图象时,单位圆的半径长与x轴的单位长度必须一致;②y=sin x,x∈[0,2π]的图象关于点P(π,0)对称;③y=cos x,x∈[0,2π]的图象关于直线x=π成轴对称图形;④正、余弦函数y=sin x和y=cos x的图象不超出直线y=-1与y=1所夹的区域.其中正确的个数为( )A.1 B.2 C.3 D.414.若锐角φ满足sin φ-cos φ=,则函数f(x)=sin2(x+φ)的单调递增区间为( )A.(k∈Z) B.(k∈Z)C.(k∈Z) D.(k∈Z) 15.如果函数![]() 的图象关于直线
的图象关于直线![]() 对称,则正实数a的最小值是( )A.
对称,则正实数a的最小值是( )A.![]() B.
B.![]() C.
C.![]() D.a=1 16.已知函数f(x)=(1-2cos2x)sin-2sin xcos xcos(-θ)在上单调递增.若f≤m恒成立,则实数m的取值范围为( )A. B. C.[1,+∞) D. 17.函数
D.a=1 16.已知函数f(x)=(1-2cos2x)sin-2sin xcos xcos(-θ)在上单调递增.若f≤m恒成立,则实数m的取值范围为( )A. B. C.[1,+∞) D. 17.函数![]() (0≤x≤9)的最大值与最小值之和为( )A.2-
(0≤x≤9)的最大值与最小值之和为( )A.2-![]() B.0 C.-1 D.-1-
B.0 C.-1 D.-1-![]() 18.已知函数f(x)=2sin ωx(ω>0)在区间[-
18.已知函数f(x)=2sin ωx(ω>0)在区间[-![]() ,
,![]() ]上的最小值是-2,则ω的最小值为 ( )A.2/3 B.1.5 C.2 D.319.已知函数f(x)=2sin的图象的一个对称中心为,其中ω为常数,且ω∈(1,3).若对任意的实数x,总有f(x1)≤f(x)≤f(x2),则|x1-x2|的最小值是( )A.1 B. C.2 D.π 20.已知函数f(x)=sin(ω>0),x∈R.若函数f(x)在区间(-ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为( )A. B.2 C. D. 二 、填空题21.函数y=tan(2x+)的单调递增区间是__________.22.函数 y=f(x) 的图象右移,横坐标缩小到原来的一半,得到y=tan2x的图象,则y=f(x)解析式是_______________.23.函数y=3-
]上的最小值是-2,则ω的最小值为 ( )A.2/3 B.1.5 C.2 D.319.已知函数f(x)=2sin的图象的一个对称中心为,其中ω为常数,且ω∈(1,3).若对任意的实数x,总有f(x1)≤f(x)≤f(x2),则|x1-x2|的最小值是( )A.1 B. C.2 D.π 20.已知函数f(x)=sin(ω>0),x∈R.若函数f(x)在区间(-ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为( )A. B.2 C. D. 二 、填空题21.函数y=tan(2x+)的单调递增区间是__________.22.函数 y=f(x) 的图象右移,横坐标缩小到原来的一半,得到y=tan2x的图象,则y=f(x)解析式是_______________.23.函数y=3-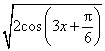 的定义域为_____. 24.方程x2=cosx的实根有________个. 25.对于函数f(x),若存在区间A=[m,n],使得{y|y=f(x),x∈A}=A,则称函数f(x)为“同域函数”,区间A为函数f(x)的一个“同域区间”.给出下列四个函数:①f(x)=cos
的定义域为_____. 24.方程x2=cosx的实根有________个. 25.对于函数f(x),若存在区间A=[m,n],使得{y|y=f(x),x∈A}=A,则称函数f(x)为“同域函数”,区间A为函数f(x)的一个“同域区间”.给出下列四个函数:①f(x)=cos![]() x;②f(x)=x2-1;③f(x)=|2x-1|;④f(x)=log2(x-1).存在“同域区间”的“同域函数”的序号是__________.(请写出所有正确结论的序号) 26.设函数
x;②f(x)=x2-1;③f(x)=|2x-1|;④f(x)=log2(x-1).存在“同域区间”的“同域函数”的序号是__________.(请写出所有正确结论的序号) 26.设函数![]() ,若存在这样的实数x1,x2,对任意的x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为 . 27.对于函数
,若存在这样的实数x1,x2,对任意的x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为 . 27.对于函数![]() ,给出下列命题:①图像关于原点成中心对称②图像关于直线
,给出下列命题:①图像关于原点成中心对称②图像关于直线![]() 对称③函数
对称③函数![]() 的最大值是3④函数的一个单调增区间是
的最大值是3④函数的一个单调增区间是![]() 其中正确命题的序号为 .28.已知函数f(x)=sin,其中ω>0.若|f(x)|≤f对x∈R恒成立,则ω的最小值为________. 29.已知函数f(x)=2sin(ω>0)的图象在区间[0,1]上恰有3个最高点,则ω的取值范围为________. 30.设函数y=sin(ωx+φ)(ω>0,φ∈(-
其中正确命题的序号为 .28.已知函数f(x)=sin,其中ω>0.若|f(x)|≤f对x∈R恒成立,则ω的最小值为________. 29.已知函数f(x)=2sin(ω>0)的图象在区间[0,1]上恰有3个最高点,则ω的取值范围为________. 30.设函数y=sin(ωx+φ)(ω>0,φ∈(-![]() ,
,![]() ))的最小正周期为π,且其图象关于直线x=
))的最小正周期为π,且其图象关于直线x=![]() 对称,则在下面四个结论:①图象关于点(
对称,则在下面四个结论:①图象关于点(![]() ,0)对称;②图象关于点(
,0)对称;②图象关于点(![]() ,0)对称;③在[0,
,0)对称;③在[0,![]() ]上是增函数;④在[-
]上是增函数;④在[-![]() ,0]上是增函数中,所有正确结
,0]上是增函数中,所有正确结![]() 论的编号为 .
论的编号为 .
答案解析1.答案为:D;2.D3.答案为:B;函数y=sin的周期T=6,当x=0时,y=,当x=1时,y=1,所以函数y=sinx+在[0,t]上至少取得2次最大值,有t-1≥T,即t≥7,所以正整数t的最小值为7.故选B.4.答案为:C;【解析】因为![]() ,又
,又![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,5.答案为:D. 6.答案为:D;∵f(x)的最小正周期是π,∴f=f=f,∵函数f(x)是偶函数,∴f=f=f=sin =.故选D.7.D8.B.解析:确定出2x-的范围,根据正弦函数的单调性求出最小值.∵x∈,∴-≤2x-≤,9.答案为:B;【解析】令
,5.答案为:D. 6.答案为:D;∵f(x)的最小正周期是π,∴f=f=f,∵函数f(x)是偶函数,∴f=f=f=sin =.故选D.7.D8.B.解析:确定出2x-的范围,根据正弦函数的单调性求出最小值.∵x∈,∴-≤2x-≤,9.答案为:B;【解析】令![]() ,即
,即![]()
![]() ,当
,当![]() 时,
时,![]() ,故选B.10.答案为:B.解析:f(x)=msin cos =msin ωx,若函数在区间上单调递增,则=≥+=,即ω∈. 11.A.
,故选B.10.答案为:B.解析:f(x)=msin cos =msin ωx,若函数在区间上单调递增,则=≥+=,即ω∈. 11.A.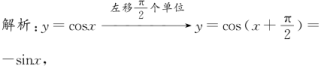 ∴g(x)=-sinx,故选A.12.答案为:B;
∴g(x)=-sinx,故选A.12.答案为:B; 13.下列叙述:①作正弦函数的图象时,单位圆的半径长与x轴的单位长度必须一致;②y=sin x,x∈[0,2π]的图象关于点P(π,0)对称;③y=cos x,x∈[0,2π]的图象关于直线x=π成轴对称图形;④正、余弦函数y=sin x和y=cos x的图象不超出直线y=-1与y=1所夹的区域.其中正确的个数为( )A.1 B.2 C.3 D.4 14.答案为:B;因为sin φ-cos φ=,所以sin=⇒φ-=⇒φ=.因为f(x)=sin2(x+φ)==,所以由2x+∈[2kπ,2kπ+π](k∈Z)得f(x)的单调递增区间为(k∈Z),故选B.15.答案为:C;【解析】由
13.下列叙述:①作正弦函数的图象时,单位圆的半径长与x轴的单位长度必须一致;②y=sin x,x∈[0,2π]的图象关于点P(π,0)对称;③y=cos x,x∈[0,2π]的图象关于直线x=π成轴对称图形;④正、余弦函数y=sin x和y=cos x的图象不超出直线y=-1与y=1所夹的区域.其中正确的个数为( )A.1 B.2 C.3 D.4 14.答案为:B;因为sin φ-cos φ=,所以sin=⇒φ-=⇒φ=.因为f(x)=sin2(x+φ)==,所以由2x+∈[2kπ,2kπ+π](k∈Z)得f(x)的单调递增区间为(k∈Z),故选B.15.答案为:C;【解析】由![]() ,当
,当![]() 时,
时,![]()
![]()
![]() ,因为
,因为![]() ,所以当
,所以当![]() 时,正数
时,正数![]() 取得最小值
取得最小值![]() ,故选C16.答案为:C;∵f(x)=(1-2cos2x)sin-2sin x·cos xcos=-cos 2x(-cos θ)-sin 2xsin θ=cos(2x+θ),当x∈时,-+θ≤2x+θ≤-+θ,∴由函数递增知解得-≤θ≤.∵f=cos,0≤+θ≤,∴f≤1.∵f≤m恒成立,∴m≥1.故选C.17.答案为:A;
,故选C16.答案为:C;∵f(x)=(1-2cos2x)sin-2sin x·cos xcos=-cos 2x(-cos θ)-sin 2xsin θ=cos(2x+θ),当x∈时,-+θ≤2x+θ≤-+θ,∴由函数递增知解得-≤θ≤.∵f=cos,0≤+θ≤,∴f≤1.∵f≤m恒成立,∴m≥1.故选C.17.答案为:A;![]() 18.B19.答案为:B;∵函数f(x)=2sin的图象的一个对称中心为,∴ω+=kπ,k∈Z,∴ω=3k-1,k∈Z,由ω∈(1,3),得ω=2.由题意得|x1-x2|的最小值为函数的半个周期,即==.故选B. 20.答案为:D.解析:因为f(x)在区间(-ω,ω)内单调递增,且函数图象关于直线x=ω对称,所以f(ω)必为一个周期上的最大值,所以有ω·ω+=2kπ+,k∈Z,所以ω2=+2kπ,k∈Z.又ω-(-ω)≤·,即ω2≤,即ω2=,所以ω=.21. ( kπ+, kπ+) (k∈Z)22.y=tan(x+)23.答案为:[
18.B19.答案为:B;∵函数f(x)=2sin的图象的一个对称中心为,∴ω+=kπ,k∈Z,∴ω=3k-1,k∈Z,由ω∈(1,3),得ω=2.由题意得|x1-x2|的最小值为函数的半个周期,即==.故选B. 20.答案为:D.解析:因为f(x)在区间(-ω,ω)内单调递增,且函数图象关于直线x=ω对称,所以f(ω)必为一个周期上的最大值,所以有ω·ω+=2kπ+,k∈Z,所以ω2=+2kπ,k∈Z.又ω-(-ω)≤·,即ω2≤,即ω2=,所以ω=.21. ( kπ+, kπ+) (k∈Z)22.y=tan(x+)23.答案为:[![]() kπ-
kπ-![]() ,
,![]() kπ+
kπ+![]()
![]() (k∈Z);
(k∈Z);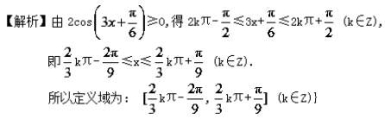 24.答案为:2解析:由函数y=x2,y=cosx的图象(如图所示),可知方程有2个实根.
24.答案为:2解析:由函数y=x2,y=cosx的图象(如图所示),可知方程有2个实根.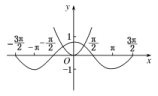 25.答案为:①②③;解析:当x∈[0,1]时,cos
25.答案为:①②③;解析:当x∈[0,1]时,cos![]() x∈[0,1],①正确;当x∈[-1,0]时,x2-1∈[-1,0],②正确;当x∈[0,1]时,|2x-1|∈[0,1],③正确;因为y=log2(x-1)为单调递增函数,所以要为“同域区间”,需满足方程log2(x-1)=x有两个根,由图象可知y=x与y=log2(x-1)没有交点,④错误. 26.答案为:2;
x∈[0,1],①正确;当x∈[-1,0]时,x2-1∈[-1,0],②正确;当x∈[0,1]时,|2x-1|∈[0,1],③正确;因为y=log2(x-1)为单调递增函数,所以要为“同域区间”,需满足方程log2(x-1)=x有两个根,由图象可知y=x与y=log2(x-1)没有交点,④错误. 26.答案为:2; 27.答案为:②③;【解析】函数
27.答案为:②③;【解析】函数![]() 的最大值为3,当
的最大值为3,当![]() 时,
时,![]() ,所以函数关于直线
,所以函数关于直线![]() 对称,当
对称,当![]() 时,
时,![]() ,所以函数不单调递增,因此正确的序号为②③. 28.答案为:4;解析:由题意得ω+=2kπ+(k∈Z),即ω=24k+4(k∈Z),由ω>0知,当k=0时,ω取到最小值4. 29.答案为:;解析:由0≤x≤1得≤ωx+≤ω+,若函数f(x)=2sin(ω>0)的图象在区间[0,1]上恰有3个最高点,根据正弦函数图象可知,应满足4π+≤ω+<6π+,解得≤ω<. 30.答案为:②④.解析:∵T=π,∴ω=2.又2×+φ=kπ+,∴φ=kπ+. ∵φ∈(-,),∴φ=,∴y=sin(2x+). 由图象及性质可知②④正确.
,所以函数不单调递增,因此正确的序号为②③. 28.答案为:4;解析:由题意得ω+=2kπ+(k∈Z),即ω=24k+4(k∈Z),由ω>0知,当k=0时,ω取到最小值4. 29.答案为:;解析:由0≤x≤1得≤ωx+≤ω+,若函数f(x)=2sin(ω>0)的图象在区间[0,1]上恰有3个最高点,根据正弦函数图象可知,应满足4π+≤ω+<6π+,解得≤ω<. 30.答案为:②④.解析:∵T=π,∴ω=2.又2×+φ=kπ+,∴φ=kπ+. ∵φ∈(-,),∴φ=,∴y=sin(2x+). 由图象及性质可知②④正确.
相关试卷
这是一份高考数学二轮复习题海集训31 椭圆(30题含答案),共9页。
这是一份高考数学二轮复习题海集训30 常用逻辑用语(30题含答案),共6页。
这是一份高考数学二轮复习题海集训19 函数f(x)=Asin(ωx+φ)+b图象性质(30题含答案),共8页。试卷主要包含了5 C,5sin的单调递减区间是等内容,欢迎下载使用。








