


所属成套资源:高考数学二轮复习题海集训 (30题含答案)
高考数学二轮复习题海集训21 平面向量的线性运算(30题含答案)
展开
这是一份高考数学二轮复习题海集训21 平面向量的线性运算(30题含答案),共8页。
2020高考数学(理数)题海集训21 平面向量的线性运算 一 、选择题1.下列各组向量中:①![]() ,
, ![]() ;②
;②![]() ,
,![]() ;③
;③![]() ,
,![]() .其中能作为表示它们所在平面内所有向量的基底的是( ) A.① B.①③ C.②③ D.①②③2.已知点O为△ABC外接圆的圆心,且++=0,则△ABC的内角A等于( )A.30° B.45° C.60° D.90° 3.与向量
.其中能作为表示它们所在平面内所有向量的基底的是( ) A.① B.①③ C.②③ D.①②③2.已知点O为△ABC外接圆的圆心,且++=0,则△ABC的内角A等于( )A.30° B.45° C.60° D.90° 3.与向量![]() 平行的单位向量为( )A.
平行的单位向量为( )A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 4.设a,b为不共线的非零向量,=2a+3b,=-8a-2b,=-6a-4b,那么( )A.与同向,且||>|| B.与同向,且||<||C.与反向,且||>|| D.∥ 5.若O、E、F是不共线的任意三点,则以下各式成立的是( )A.=+ B.=- C.=-+ D.=-- 6.已知a,b是两个非零向量,且|a+b|=|a|+|b|,则下列说法正确的是( )A.a+b=0 B.a=bC.a与b反向共线 D.存在正实数λ,使得a=λb 7.已知平行四边形三个顶点的坐标分别为(-1,0),(3,0),(1,-5),则第四个点的坐标为( ) A.(1,5)或(5,-5) B.(1,5)或(-3,-5) C.(5,-5)或(-3,-5) D.(1,5)或(-3,-5)或(5,-5) 8.a、b为非零向量,且|a+b|=|a|+|b|,则( )A.a∥b,且a与b方向相同 B.a、b是方向相反的向量C.a=-b D.a、b无论什么关系均可 9.已知||=5,||=7,则|-|的取值范围是( )A.[2,12] B.(2,12) C.[2,7] D.(2,7) 10.当a,b满足下列何种条件时,等式|a+b|=|a|-|b|成立( ).A.a与b同向 B.a与b反向C.a与b同向且|a|≤|b| D.a与b反向且|a|≥|b| 11.下列向量的运算结果为零向量的是( )A.
4.设a,b为不共线的非零向量,=2a+3b,=-8a-2b,=-6a-4b,那么( )A.与同向,且||>|| B.与同向,且||<||C.与反向,且||>|| D.∥ 5.若O、E、F是不共线的任意三点,则以下各式成立的是( )A.=+ B.=- C.=-+ D.=-- 6.已知a,b是两个非零向量,且|a+b|=|a|+|b|,则下列说法正确的是( )A.a+b=0 B.a=bC.a与b反向共线 D.存在正实数λ,使得a=λb 7.已知平行四边形三个顶点的坐标分别为(-1,0),(3,0),(1,-5),则第四个点的坐标为( ) A.(1,5)或(5,-5) B.(1,5)或(-3,-5) C.(5,-5)或(-3,-5) D.(1,5)或(-3,-5)或(5,-5) 8.a、b为非零向量,且|a+b|=|a|+|b|,则( )A.a∥b,且a与b方向相同 B.a、b是方向相反的向量C.a=-b D.a、b无论什么关系均可 9.已知||=5,||=7,则|-|的取值范围是( )A.[2,12] B.(2,12) C.[2,7] D.(2,7) 10.当a,b满足下列何种条件时,等式|a+b|=|a|-|b|成立( ).A.a与b同向 B.a与b反向C.a与b同向且|a|≤|b| D.a与b反向且|a|≥|b| 11.下列向量的运算结果为零向量的是( )A.![]() +
+![]() B.
B.![]() +
+![]() +
+![]() C.
C.![]() +
+![]() +
+![]() +
+![]() D.
D.![]() +
+![]() +
+![]() +
+![]() 12.已知a,b是不共线的两个向量,向量=λa+b,=a+μb(λ,μ∈R),则A,B,C三点共线的充要条件为( )A.λ+μ=2 B.λ-μ=1 C.λμ=1 D.λμ=-1 13.已知下列各式:①A+M+B;②A+C+B+D;③O+O+B+C.其中结果为零向量的个数为( )A.0 B.1 C.2 D.3 14.向量
12.已知a,b是不共线的两个向量,向量=λa+b,=a+μb(λ,μ∈R),则A,B,C三点共线的充要条件为( )A.λ+μ=2 B.λ-μ=1 C.λμ=1 D.λμ=-1 13.已知下列各式:①A+M+B;②A+C+B+D;③O+O+B+C.其中结果为零向量的个数为( )A.0 B.1 C.2 D.3 14.向量![]() 满足
满足![]() ,则
,则![]() 与
与![]() 的夹角为( )A.
的夹角为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 15.已知点M是△ABC的边BC的中点,点E在边AC上,且
15.已知点M是△ABC的边BC的中点,点E在边AC上,且![]() ,则向量
,则向量![]() =( )
=( ) A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 16.已知复数z=1+2i,则
16.已知复数z=1+2i,则![]() =( )A.5 B.5+4i C.﹣3 D.3﹣4i 17.若
=( )A.5 B.5+4i C.﹣3 D.3﹣4i 17.若![]() 为
为![]() 所在平面内任一点,且满足
所在平面内任一点,且满足![]() ,则
,则![]() 的形状为( )A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形 18.如图所示,
的形状为( )A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形 18.如图所示,![]() ,
,![]() ,
,![]() 是圆
是圆![]() 上不同的三点,线段
上不同的三点,线段![]() 的延长线与线段
的延长线与线段![]() 交于圆外的一点
交于圆外的一点![]() ,若
,若![]() (
(![]() ,
,![]() ),则
),则![]() 的取值范围是( )
的取值范围是( )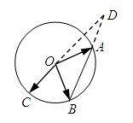 A.
A.![]() B.
B.![]() C.
C.![]() D.
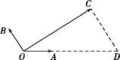
D.![]() 19.已知:如图,|
19.已知:如图,|![]() |=|
|=|![]() |=1,
|=1,![]() 与
与![]() 的夹角为120°,
的夹角为120°,![]() 与
与![]() 的夹角为30°,若
的夹角为30°,若![]() =λ
=λ![]() +μ
+μ![]() (λ、μ∈R),则
(λ、μ∈R),则![]() 等于( )
等于( )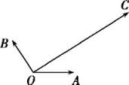 A.
A.![]() B.
B.![]() C.
C.![]() D.220.已知
D.220.已知![]() ,向量
,向量![]() ,则实数
,则实数![]() 的值为( )A.
的值为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二 、填空题21.如图所示,△ABC中,
二 、填空题21.如图所示,△ABC中,![]() ,且BC=3,则|+|=________.
,且BC=3,则|+|=________.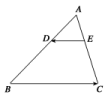 22.若a≠0,b≠0,且|a|=|b|=|a-b|,则a与a+b所在直线的夹角是________. 23.给出下列命题:①若+=,则-=; ②若+=,则+=;③若+=,则-=; ④若+=,则+=.其中所有正确命题的序号为________. 24.在矩形ABCD中,若AB=3,BC=2,则|
22.若a≠0,b≠0,且|a|=|b|=|a-b|,则a与a+b所在直线的夹角是________. 23.给出下列命题:①若+=,则-=; ②若+=,则+=;③若+=,则-=; ④若+=,则+=.其中所有正确命题的序号为________. 24.在矩形ABCD中,若AB=3,BC=2,则|![]() +
+![]() |=__________. 25.已知||=||=
|=__________. 25.已知||=||=![]() ,且∠AOB=120°,则|+|=________. 26.在直角梯形ABCD中,∠A=90°,∠B=30°,AB=2,BC=2,点E在线段CD上,若=+μ,则μ的取值范围是________. 27.在△ABC中,∠A=60°,∠A的平分线交BC于点D,若AB=4,且=+λ (λ∈R),则AD的长为________. 28.设向量
,且∠AOB=120°,则|+|=________. 26.在直角梯形ABCD中,∠A=90°,∠B=30°,AB=2,BC=2,点E在线段CD上,若=+μ,则μ的取值范围是________. 27.在△ABC中,∠A=60°,∠A的平分线交BC于点D,若AB=4,且=+λ (λ∈R),则AD的长为________. 28.设向量![]() =(1,x),
=(1,x),![]() =(x,1),若
=(x,1),若![]() •
•![]() =﹣|
=﹣|![]() |•|
|•|![]() |,则x= . 29.已知向量
|,则x= . 29.已知向量![]() 与
与![]() 的夹角是
的夹角是![]() ,且|
,且|![]() |=2,|
|=2,|![]() |=3,若(2
|=3,若(2![]() +λ
+λ![]() )⊥
)⊥![]() ,则实数λ= . 30.设向量
,则实数λ= . 30.设向量![]() =(﹣1,2),
=(﹣1,2),![]() =(m,1),如果向量
=(m,1),如果向量![]() +2
+2![]() 与2
与2![]() ﹣
﹣![]() 平行,则
平行,则![]() +
+![]() = .
= .
答案解析1.A2.答案为:A;由++=0得,+=,由O为△ABC外接圆的圆心,结合向量加法的几何意义知,四边形OACB为菱形,且∠CAO=60°,故A=30°. 3.C4.答案为:A.解析:=++=2a+3b+(-8a-2b)+(-6a-4b)=-12a-3b,又=-8a-2b,∴=.∵>0,∴与同向,且||=||>||.∴||>||. 5.答案为:B;解析:=+=-,故选B.6.答案为:D;由已知得,向量a与b为同向向量,即存在正实数λ,使得a=λb,故选D. 7.D8.答案为:A;解析:只有a∥b,且a与b方向相同时才有|a+b|=|a|+|b|成立.故A项正确.9.答案为:A;解析:与同向时,|-|=||-||=7-5=2,当与反向时,|-|=||+||=7+5=12,故选A.10.答案为:D;解析:当a与b反向且|a|≥|b|时,|a+b|=|a|-|b|.11.答案为:D;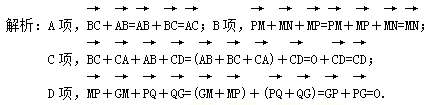 12.答案为:C.解析:∵向量a和b不共线,∴和为非零向量,则A,B,C三点共线的充要条件为存在k(k≠0),使得=k,即λa+b=k(a+μb)=ka+kμb,∵a和b不共线,∴λ=k,1=kμ,∴λμ=1,故选C. 13.答案为:C;14.答案为:A15.答案为:B16.A解:∵z=1+2i,∴
12.答案为:C.解析:∵向量a和b不共线,∴和为非零向量,则A,B,C三点共线的充要条件为存在k(k≠0),使得=k,即λa+b=k(a+μb)=ka+kμb,∵a和b不共线,∴λ=k,1=kμ,∴λμ=1,故选C. 13.答案为:C;14.答案为:A15.答案为:B16.A解:∵z=1+2i,∴![]() =|z|2=
=|z|2=![]() .故选:A.17.B 18.D∵
.故选:A.17.B 18.D∵![]() ,
,![]() ,∴
,∴![]() ,展开得
,展开得![]() ,∴
,∴![]() ,当
,当![]() 时,
时,![]() 即
即![]() ,∴
,∴![]() .当
.当![]() 趋近于射线
趋近于射线![]() 时,由平行四边形法则可知
时,由平行四边形法则可知![]() ,此时
,此时![]() 且
且![]() ,∴
,∴![]() ,因此
,因此![]() 的取值范围是
的取值范围是![]() ,故选D.
,故选D.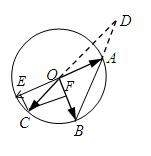 19.答案为:D;
19.答案为:D;
 20.C 21.答案为:
20.C 21.答案为:![]() ;
; 14.答案为:2
14.答案为:2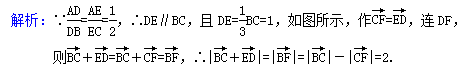
 22.答案为:30°23.答案为:①②③④;解析:若O+O=O,则O=O-O,故①正确;若O+O=O,则O-O=O+D=O,故②正确;若O+O=O,则O-E=O,故③正确;若O+O=O,则-O-O=-O,即D+E=M,故④正确.24.答案为:
22.答案为:30°23.答案为:①②③④;解析:若O+O=O,则O=O-O,故①正确;若O+O=O,则O-O=O+D=O,故②正确;若O+O=O,则O-E=O,故③正确;若O+O=O,则-O-O=-O,即D+E=M,故④正确.24.答案为:![]() ;
;![]() 25.答案为:
25.答案为:![]() ;解析:以,为邻边作▱OACB,∵||=||,∴▱OACB为菱形,∴|+|=||,∵∠AOB=120°,∴△OAC为正三角形,∴||=
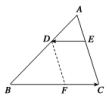
;解析:以,为邻边作▱OACB,∵||=||,∴▱OACB为菱形,∴|+|=||,∵∠AOB=120°,∴△OAC为正三角形,∴||=![]() .26.答案为:;解析:由题意可求得AD=1,CD=,所以=2.∵点E在线段CD上,∴=λ (0≤λ≤1).∵=+,又=+μ=+2μ=+,∴=1,即μ=.∵0≤λ≤1,∴0≤μ≤,即μ的取值范围是. 27.答案为:3;解析:因为B,D,C三点共线,所以+λ=1,解得λ=,如图,过点D分别作AC,AB的平行线交AB,AC于点M,N,则=,=,经计算得AN=AM=3,AD=3.
.26.答案为:;解析:由题意可求得AD=1,CD=,所以=2.∵点E在线段CD上,∴=λ (0≤λ≤1).∵=+,又=+μ=+2μ=+,∴=1,即μ=.∵0≤λ≤1,∴0≤μ≤,即μ的取值范围是. 27.答案为:3;解析:因为B,D,C三点共线,所以+λ=1,解得λ=,如图,过点D分别作AC,AB的平行线交AB,AC于点M,N,则=,=,经计算得AN=AM=3,AD=3.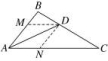 28.答案为:解:
28.答案为:解:![]() ,
,![]() ;∴由
;∴由![]() 得:2x=﹣(x2+1);解得x=﹣1.故答案为:﹣1.29.答案为:﹣
得:2x=﹣(x2+1);解得x=﹣1.故答案为:﹣1.29.答案为:﹣![]() .解:向量
.解:向量![]() 与
与![]() 的夹角是
的夹角是![]() ,且|
,且|![]() |=2,|
|=2,|![]() |=3,(2
|=3,(2![]() +λ
+λ![]() )⊥
)⊥![]() ,则(2
,则(2![]() +λ
+λ![]() )•
)•![]() =2
=2![]() +λ
+λ![]() =2×2×3×cos
=2×2×3×cos![]() +9λ=0,解得λ=﹣
+9λ=0,解得λ=﹣![]() ,故答案为:﹣
,故答案为:﹣![]() 30.解:
30.解:![]() +2
+2![]() =(2m﹣1,4),2
=(2m﹣1,4),2![]() ﹣
﹣![]() =(﹣2﹣m,3),∵
=(﹣2﹣m,3),∵![]() +2
+2![]() 与2
与2![]() ﹣
﹣![]() 平行,∴4(﹣2﹣m)﹣3(2m﹣1)=0,解得m=﹣0.5,则
平行,∴4(﹣2﹣m)﹣3(2m﹣1)=0,解得m=﹣0.5,则![]() +
+![]() =
=![]() .故答案为:(-1.5,3).
.故答案为:(-1.5,3).
相关试卷
这是一份高考数学二轮复习题海集训34 导数的计算(30题含答案),共6页。
这是一份高考数学二轮复习题海集训32 双曲线(30题含答案),共10页。试卷主要包含了故选C,由左焦点F,等内容,欢迎下载使用。
这是一份高考数学二轮复习题海集训31 椭圆(30题含答案),共9页。








