


所属成套资源:高考数学二轮复习题海集训 (30题含答案)
高考数学二轮复习题海集训24 正弦定理余弦定理(30题含答案)
展开
这是一份高考数学二轮复习题海集训24 正弦定理余弦定理(30题含答案),共7页。
2020高考数学(理数)题海集训24 正弦定理余弦定理 一 、选择题1.△ABC的外接圆半径为R,C=60°,则![]() 的取值范围是( )A.[
的取值范围是( )A.[![]() ,2
,2![]() ] B.[
] B.[![]() ,2
,2![]() ) C.(
) C.(![]() ,2
,2![]() ] D.(
] D.(![]() ,2
,2![]() ) 2.在△ABC中,sinA=
) 2.在△ABC中,sinA=![]() ,a=10,边长c的取值范围是( )A.(
,a=10,边长c的取值范围是( )A.(![]() ,+∞) B.(10,+∞) C.(0,10) D.(0,
,+∞) B.(10,+∞) C.(0,10) D.(0,![]() ] 3.在△ABC中,已知a:b:c=3:5:7,则这个三角形最大角的外角是( )A.30° B.60° C.90° D.120°4.在△ABC中,已知a=2,则
] 3.在△ABC中,已知a:b:c=3:5:7,则这个三角形最大角的外角是( )A.30° B.60° C.90° D.120°4.在△ABC中,已知a=2,则![]() 等于( )A.1 B.
等于( )A.1 B.![]() C.2 D.45.△ABC中,内角A,B,C对应的边分别为a,b,c,c=2a,bsin B-asin A=asin C,则sin B的值为( )A. B. C. D. 6.在△ABC中,
C.2 D.45.△ABC中,内角A,B,C对应的边分别为a,b,c,c=2a,bsin B-asin A=asin C,则sin B的值为( )A. B. C. D. 6.在△ABC中,![]() 则角B=( )A.
则角B=( )A.![]() B.
B.![]() C .
C .![]() D.
D.![]() 7.在△ABC中,sin2A≤sin2B+sin2C-sin Bsin C,则A的取值范围是( )A. B. C. D. 8.△ABC的内角A,B,C所对的边分别为a,b,c,已知b=,c=4,cos B=,则△ABC的面积为( )A.3 B. C.9 D. 9.在△ABC中,下列等式中总能成立的是( )A.asinA=bsinB B.bsinC=csinA C.absinC=bcsinB D.absinC=bcsinA 10.在△ABC中,∠C=60°,AC=2,BC=3,那么AB=( )A. B. C. D.2 11.在△ABC中,内角A,B,C的对边分别为a,b,c,若asin Bcos C+csin Bcos A=b,且a>b,则B=( )A. B. C. D.12.若△ABC内角A,B,C对边分别为a,b,c,且
7.在△ABC中,sin2A≤sin2B+sin2C-sin Bsin C,则A的取值范围是( )A. B. C. D. 8.△ABC的内角A,B,C所对的边分别为a,b,c,已知b=,c=4,cos B=,则△ABC的面积为( )A.3 B. C.9 D. 9.在△ABC中,下列等式中总能成立的是( )A.asinA=bsinB B.bsinC=csinA C.absinC=bcsinB D.absinC=bcsinA 10.在△ABC中,∠C=60°,AC=2,BC=3,那么AB=( )A. B. C. D.2 11.在△ABC中,内角A,B,C的对边分别为a,b,c,若asin Bcos C+csin Bcos A=b,且a>b,则B=( )A. B. C. D.12.若△ABC内角A,B,C对边分别为a,b,c,且![]() ,则
,则![]() 等于( )A.
等于( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 13.△ABC的内角A,B,C所对的边分别为a,b,c.若B=2A,a=1,b=
13.△ABC的内角A,B,C所对的边分别为a,b,c.若B=2A,a=1,b=![]() ,则c=( )A.2
,则c=( )A.2![]() B.2 C.
B.2 C.![]() D.1 14.设△ABC的内角A,B,C所对的边分别为a,b,c.若a=3,b=,A=,则B=( )A. B. C.或 D. 15.在△ABC中,角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定 16.在△ABC中,sin2A=sin2B+sin2C,则△ABC为( )A.直角三角形 B.等腰直角三角形 C.等边三角形 D.等腰三角形 17.在钝角△ABC中,角A,B,C所对的边分别为a,b,c,B为钝角,若acos A=bsin A,则sin A+sin C的最大值为( )A. B. C.1 D. 18.在△ABC中,角A、B、C的对边分别为a、b、c.若(a2+c2-b2)tanB=
D.1 14.设△ABC的内角A,B,C所对的边分别为a,b,c.若a=3,b=,A=,则B=( )A. B. C.或 D. 15.在△ABC中,角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定 16.在△ABC中,sin2A=sin2B+sin2C,则△ABC为( )A.直角三角形 B.等腰直角三角形 C.等边三角形 D.等腰三角形 17.在钝角△ABC中,角A,B,C所对的边分别为a,b,c,B为钝角,若acos A=bsin A,则sin A+sin C的最大值为( )A. B. C.1 D. 18.在△ABC中,角A、B、C的对边分别为a、b、c.若(a2+c2-b2)tanB=![]() ac,则角B的值为( )A.
ac,则角B的值为( )A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]() 19.在△ABC中,角A,B,C所对边分别为a,b,c,且2sinCcosB=2sinA+sinB,c=3ab,则ab最小值是( )A.
19.在△ABC中,角A,B,C所对边分别为a,b,c,且2sinCcosB=2sinA+sinB,c=3ab,则ab最小值是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 20.在△ABC中,内角A,B,C所对边分别是a,b,c,若3a=2b,则
20.在△ABC中,内角A,B,C所对边分别是a,b,c,若3a=2b,则![]() 值为( ) A.
值为( ) A.![]() B.
B.![]() C.1 D.
C.1 D.![]() 二 、填空题21.△ABC中,a,b,c分别是角A、B、C的对边,若
二 、填空题21.△ABC中,a,b,c分别是角A、B、C的对边,若![]() ,则B的值为____________.22.已知三角形的两角分别是45°、60°,它们夹边的长是1,则最小边长为________. 23.已知△ABC中,
,则B的值为____________.22.已知三角形的两角分别是45°、60°,它们夹边的长是1,则最小边长为________. 23.已知△ABC中,![]() 交BC于D,则AD的长为 . 24.已知在△ABC中,角A,B,C的对边分别为a,b,c,若a=+,A=75°,cos B=,则b=________. 25.在锐角△ABC中,D为BC的中点,满足∠BAD+∠C=90°,则∠B,∠C的大小关系是________. 26.在△ABC中,sin2A≤sin2B+sin2C-sin Bsin C,则A的取值范围是__ _____.27.在△ABC中,角A,B,C所对边分别为a,b,c,
交BC于D,则AD的长为 . 24.已知在△ABC中,角A,B,C的对边分别为a,b,c,若a=+,A=75°,cos B=,则b=________. 25.在锐角△ABC中,D为BC的中点,满足∠BAD+∠C=90°,则∠B,∠C的大小关系是________. 26.在△ABC中,sin2A≤sin2B+sin2C-sin Bsin C,则A的取值范围是__ _____.27.在△ABC中,角A,B,C所对边分别为a,b,c, ![]() 若
若![]() ,则角C=__________.28.设△ABC三边长分别为15,19,23,现将三边长各减去x后,得一钝角三角形,则x的范围为________. 29.在△ABC中,内角A,B,C的对边分别为a,b,c,已知c=5,B=,△ABC的面积为,则cos 2A=________. 30.在△ABC中,角A,B,C的对边分别是a,b,c,若
,则角C=__________.28.设△ABC三边长分别为15,19,23,现将三边长各减去x后,得一钝角三角形,则x的范围为________. 29.在△ABC中,内角A,B,C的对边分别为a,b,c,已知c=5,B=,△ABC的面积为,则cos 2A=________. 30.在△ABC中,角A,B,C的对边分别是a,b,c,若![]() 且
且![]() 则△ABC的面积等于________.
则△ABC的面积等于________.
答案解析1.2.答案为:D 3.答案为:B;4.答案为:C;5.答案为:C;解析:由正弦定理,得b2-a2=ac,又c=2a,所以b2=2a2,所以cos B==,所以sin B=. 6.答案为:A;7.答案为:C.解析:由正弦定理及sin2A≤sin2B+sin2C-sin Bsin C可得a2≤b2+c2-bc,即b2+c2-a2≥bc,由余弦定理可得cos A=≥=,又0<A<π,所以0<A≤.故A的取值范围是.故选C. 8.答案为:B.解析:由余弦定理b2=c2+a2-2accos B,得7=16+a2-6a,解得a=3,∵cos B=,∴sin B=,∴S△ABC=casin B=×4×3×=.故选B. 9.答案为:D 10.答案为:C;解析:由余弦定理得AB2=22+32-2×2×3×cos 60°=7,∴AB=,故选C. 11.答案为:A;解析:∵asin Bcos C+csin Bcos A=b,∴根据正弦定理可得sin Asin Bcos C+sin Csin Bcos A=sin B,即sin B(sin Acos C+sin Ccos A)=sin B.∵sin B≠0,∴sin(A+C)=,即sin B=.∵a>b,∴A>B,即B为锐角,∴B=,故选A. 12.答案为:B; 13.答案为:B解析: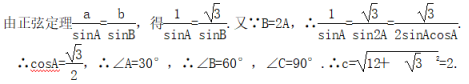 14.答案为:A;解析:由正弦定理得=,∴sin B=,∴B=或B=,又b<a,∴B<A,∴B=.故选A. 15.答案为:B;解析:由已知及正弦定理得sin Bcos C+sin Ccos B=sin2A,即sin(B+C)=sin2A,又sin(B+C)=sin A,∴sin A=1,∴A=.故选B. 16.答案为:A 17.答案为:B;解析:∵acos A=bsin A,由正弦定理可得,sin Acos A=sin Bsin A,∵sin A≠0,∴cos A=sin B,又B为钝角,∴B=A+,sin A+sin C=sin A+sin(A+B)=sin A+cos 2A=sin A+1-2sin2A=-22+,∴sin A+sin C的最大值为. 18.答案为:D; 19.B.
14.答案为:A;解析:由正弦定理得=,∴sin B=,∴B=或B=,又b<a,∴B<A,∴B=.故选A. 15.答案为:B;解析:由已知及正弦定理得sin Bcos C+sin Ccos B=sin2A,即sin(B+C)=sin2A,又sin(B+C)=sin A,∴sin A=1,∴A=.故选B. 16.答案为:A 17.答案为:B;解析:∵acos A=bsin A,由正弦定理可得,sin Acos A=sin Bsin A,∵sin A≠0,∴cos A=sin B,又B为钝角,∴B=A+,sin A+sin C=sin A+sin(A+B)=sin A+cos 2A=sin A+1-2sin2A=-22+,∴sin A+sin C的最大值为. 18.答案为:D; 19.B. 20.答案为:D;
20.答案为:D; 21.答案为:
21.答案为:![]() ;解析:由正弦定理可将
;解析:由正弦定理可将![]() 转化为
转化为![]() ,经计算
,经计算![]() 得
得![]() ,又
,又![]() 为
为![]() 内角,可知
内角,可知![]() ,则
,则![]() .22.答案为:
.22.答案为:![]() -1; 23.答案为:
-1; 23.答案为: ![]() ;
; 24.答案为:2;解析:在△ABC中,由cos B=,可得sin B=,由A=75°,可得sin A=,根据正弦定理=,得=,解得b=2.25.答案为:∠B=∠C;解析:由∠BAD+∠C=90°,得∠CAD+∠B=90°,由正弦定理得==,==,又D为BC的中点,所以BD=DC,所以=,化简得sin Bcos B=sin CcosC,即sin 2B=sin 2C,又△ABC为锐角三角形,所以∠B=∠C.26.答案为:(0,
24.答案为:2;解析:在△ABC中,由cos B=,可得sin B=,由A=75°,可得sin A=,根据正弦定理=,得=,解得b=2.25.答案为:∠B=∠C;解析:由∠BAD+∠C=90°,得∠CAD+∠B=90°,由正弦定理得==,==,又D为BC的中点,所以BD=DC,所以=,化简得sin Bcos B=sin CcosC,即sin 2B=sin 2C,又△ABC为锐角三角形,所以∠B=∠C.26.答案为:(0,![]() ];27.答案为:
];27.答案为:![]() 28.答案为:(3,11)解析:由两边之和大于第三边,得15-x+19-x>23-x,∴x<11.①又因得到的三角形为钝角三角形,∴(15-x)2+(19-x)2<(23-x)2.即x2-22x+57<0,(x-3)(x-19)<0,3<x<19.②由①、②可得3<x<11.29.答案为:;解析:由三角形的面积公式,得S△ABC=acsin B=×a×5×sin=××5a=,解得a=3.由b2=a2+c2-2accos B=32+52-2×3×5×=49,得b=7.由=⇒sin A=sin B=sin=,∴cos 2A=1-2sin2A=1-2×2=.30.答案为:
28.答案为:(3,11)解析:由两边之和大于第三边,得15-x+19-x>23-x,∴x<11.①又因得到的三角形为钝角三角形,∴(15-x)2+(19-x)2<(23-x)2.即x2-22x+57<0,(x-3)(x-19)<0,3<x<19.②由①、②可得3<x<11.29.答案为:;解析:由三角形的面积公式,得S△ABC=acsin B=×a×5×sin=××5a=,解得a=3.由b2=a2+c2-2accos B=32+52-2×3×5×=49,得b=7.由=⇒sin A=sin B=sin=,∴cos 2A=1-2sin2A=1-2×2=.30.答案为:![]()
相关试卷
这是一份高考数学二轮复习题海集训34 导数的计算(30题含答案),共6页。
这是一份高考数学二轮复习题海集训32 双曲线(30题含答案),共10页。试卷主要包含了故选C,由左焦点F,等内容,欢迎下载使用。
这是一份高考数学二轮复习题海集训31 椭圆(30题含答案),共9页。








