


所属成套资源:高考数学二轮复习题海集训 (30题含答案)
高考数学二轮复习题海集训34 导数的计算(30题含答案)
展开
这是一份高考数学二轮复习题海集训34 导数的计算(30题含答案),共6页。
2020高考数学(理数)题海集训34 导数的计算一 、选择题1.曲线y=![]() x3在x=1处切线的倾斜角为( )A.1 B.-
x3在x=1处切线的倾斜角为( )A.1 B.-![]() C.
C.![]() D.
D.![]() 2.一木块沿某一斜面自由下滑,测得下滑的水平距离s与时间t之间的函数关系为s=
2.一木块沿某一斜面自由下滑,测得下滑的水平距离s与时间t之间的函数关系为s=![]() t2,则t=2s时,此木块在水平方向的瞬时速度为( )A.1 B.0.125 C.0.5 D.0.25 3.函数y=f(x),当自变量从x0到x1时,函数值的增量与相应自变量的增量之比是函数( )A.在区间[x0,x1]上的平均变化率 B.在x0处的变化率C.在x1处的变化率 D.在[x0,x1]上的变化率 4.直线y=x+b是曲线y=ln x(x>0)的一条切线,则实数b的值为( )A.2 B.ln 2+1 C.ln 2-1 D.ln 2 5.曲线f(x)=在点(1,f(1))处切线的倾斜角为,则实数a=( )A.1 B.-1 C.7 D.-7 6.函数f(x)=(x+2a)(x-a)2的导数为( )A.2(x2-a2) B.2(x2+a2)C.3(x2-a2) D.3(x2+a2) 7.已知物体的运动方程为
t2,则t=2s时,此木块在水平方向的瞬时速度为( )A.1 B.0.125 C.0.5 D.0.25 3.函数y=f(x),当自变量从x0到x1时,函数值的增量与相应自变量的增量之比是函数( )A.在区间[x0,x1]上的平均变化率 B.在x0处的变化率C.在x1处的变化率 D.在[x0,x1]上的变化率 4.直线y=x+b是曲线y=ln x(x>0)的一条切线,则实数b的值为( )A.2 B.ln 2+1 C.ln 2-1 D.ln 2 5.曲线f(x)=在点(1,f(1))处切线的倾斜角为,则实数a=( )A.1 B.-1 C.7 D.-7 6.函数f(x)=(x+2a)(x-a)2的导数为( )A.2(x2-a2) B.2(x2+a2)C.3(x2-a2) D.3(x2+a2) 7.已知物体的运动方程为![]() (t是时间,s是位移),则物体在时刻t=2时的速度为( )A.
(t是时间,s是位移),则物体在时刻t=2时的速度为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.若曲线f(x)=acos x与曲线g(x)=x2+bx+1在交点(0,m)处有公切线,则a+b=( )A.-1 B.0 C.1 D.2 9.已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
8.若曲线f(x)=acos x与曲线g(x)=x2+bx+1在交点(0,m)处有公切线,则a+b=( )A.-1 B.0 C.1 D.2 9.已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )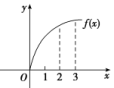 A.0<f′(2)<f′(3)<f(3)-f(2)B.0<f′(3)<f′(2)<f(3)-f(2)C.0<f′(3)<f(3)-f(2)<f′(2)D.0<f(3)-f(2)<f′(2)<f′(3) 10.某质点的位移函数是s(t)=2t3-
A.0<f′(2)<f′(3)<f(3)-f(2)B.0<f′(3)<f′(2)<f(3)-f(2)C.0<f′(3)<f(3)-f(2)<f′(2)D.0<f(3)-f(2)<f′(2)<f′(3) 10.某质点的位移函数是s(t)=2t3-![]() gt2(g=10 m/s2),则当t=2 s时,它的加速度是( )A.14 m/s2 B.4 m/s2 C.10 m/s2 D.-4 m/s2 11.若f(x)=xex,则f′(1)=( )A.0 B.e C.2e D.e2 12.f(x)与g(x)是定义在R上的两个可导函数,若f(x),g(x)满足f′(x)=g′(x),则f(x)与g(x)满足( )A.f(x)=g(x) B.f(x)=g(x)=0C.f(x)-g(x)为常数函数 D.f(x)+g(x)为常数函数 13.已知函数f(x)=x+lnx,则f′(1)=( ) A.1 B.﹣2 C.﹣1 D.214.已知曲线y=x3-1与曲线y=3-0.5x2在x=x0处的切线互相垂直,则x0的值为( )A.
gt2(g=10 m/s2),则当t=2 s时,它的加速度是( )A.14 m/s2 B.4 m/s2 C.10 m/s2 D.-4 m/s2 11.若f(x)=xex,则f′(1)=( )A.0 B.e C.2e D.e2 12.f(x)与g(x)是定义在R上的两个可导函数,若f(x),g(x)满足f′(x)=g′(x),则f(x)与g(x)满足( )A.f(x)=g(x) B.f(x)=g(x)=0C.f(x)-g(x)为常数函数 D.f(x)+g(x)为常数函数 13.已知函数f(x)=x+lnx,则f′(1)=( ) A.1 B.﹣2 C.﹣1 D.214.已知曲线y=x3-1与曲线y=3-0.5x2在x=x0处的切线互相垂直,则x0的值为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 15.已知函数fn(x)=xn+1,n∈N的图象与直线x=1交于点P,若图象在点P处的切线与x轴交点的横坐标为xn,则log2 020x1+log2 020x2+…+log2 020x2 019的值为( )A.-1 B.1-log2 0202 019 C.-log2 0192 018 D.1 16.若函数y=f(x)在区间(a,b)内可导,且x0∈(a,b),则
15.已知函数fn(x)=xn+1,n∈N的图象与直线x=1交于点P,若图象在点P处的切线与x轴交点的横坐标为xn,则log2 020x1+log2 020x2+…+log2 020x2 019的值为( )A.-1 B.1-log2 0202 019 C.-log2 0192 018 D.1 16.若函数y=f(x)在区间(a,b)内可导,且x0∈(a,b),则 ![]() 的值为( )A.f'(x0) B.2f'(x0) C.-2f'(x0) D.0 17.设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处的切线的斜率为( )A.4 B.-0.25 C.2 D.-0.5 18.已知函数f(x)=
的值为( )A.f'(x0) B.2f'(x0) C.-2f'(x0) D.0 17.设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处的切线的斜率为( )A.4 B.-0.25 C.2 D.-0.5 18.已知函数f(x)=![]() cos x,则f(π)+f /
cos x,则f(π)+f /![]() =( )A.-
=( )A.- ![]() B.-
B.- ![]() C.-
C.- ![]() D.-
D.- ![]() 19.设f(x)=xln x,若f′(x0)=2,则x0的值为( )A.e2 B.e C.
19.设f(x)=xln x,若f′(x0)=2,则x0的值为( )A.e2 B.e C.![]() D.ln 2 20.若存在过点(1,0)的直线与曲线y=x3和y=ax2+
D.ln 2 20.若存在过点(1,0)的直线与曲线y=x3和y=ax2+![]() x-9都相切,则a等于( )A.-1或-
x-9都相切,则a等于( )A.-1或-![]() B.-1或
B.-1或![]() C.-
C.-![]() 或-
或-![]() D.-
D.-![]() 或7 二 、填空题21.已知函数y=f(x)=x2+1,在x=2,△x=0.1时,△y的值为________. 22.某物体作直线运动,其运动规律是
或7 二 、填空题21.已知函数y=f(x)=x2+1,在x=2,△x=0.1时,△y的值为________. 22.某物体作直线运动,其运动规律是![]() (t的单位是秒,s的单位是米),则它在第4秒末的瞬时速度应该为________ m/s. 23.曲线y=x(x-1)(x-2)…(x-6)在原点处的切线方程为__________. 24.已知函数f(x)=x4+ax2-bx,且f'(0)=-13,f'(-1)=-27,则a+b=________. 25.曲线y=2ln x在点(1,0)处的切线方程为________. 26.函数f(x)=8x-6在区间[m,n]上的平均变化率为________. 27.曲线y=cos x在点A(
(t的单位是秒,s的单位是米),则它在第4秒末的瞬时速度应该为________ m/s. 23.曲线y=x(x-1)(x-2)…(x-6)在原点处的切线方程为__________. 24.已知函数f(x)=x4+ax2-bx,且f'(0)=-13,f'(-1)=-27,则a+b=________. 25.曲线y=2ln x在点(1,0)处的切线方程为________. 26.函数f(x)=8x-6在区间[m,n]上的平均变化率为________. 27.曲线y=cos x在点A(![]() )处的切线方程为__________________. 28.曲线y=x2上切线倾斜角为
)处的切线方程为__________________. 28.曲线y=x2上切线倾斜角为![]() 的点是__________. 29.在平面直角坐标系xOy中,若曲线y=
的点是__________. 29.在平面直角坐标系xOy中,若曲线y=![]() (a,b为常数)过点P(2,-5),且该曲线在点P处的切线与直线7x+2y+3=0平行,则a+b的值是______. 30.若函数f(x)=x2-ax+ln x存在垂直于y轴的切线,则实数a的取值范围是________.
(a,b为常数)过点P(2,-5),且该曲线在点P处的切线与直线7x+2y+3=0平行,则a+b的值是______. 30.若函数f(x)=x2-ax+ln x存在垂直于y轴的切线,则实数a的取值范围是________.
0.2020高考数学(理数)题海集训34 导数的计算(30题含答案)答案解析 一 、选择题1. [答案]C. 2. [答案]C; 3. [答案] A 4.答案为:C;∵y=ln x的导数为y′=,∴=,解得x=2,∴切点为(2,ln 2).将其代入直线y=x+b,得b=ln 2-1. 5.答案为:C;解析:选C.f′(x)==,又∵f′(1)=tan=-1,∴a=7. 6.答案为:C;解析:f′(x)=(x-a)2+(x+2a)[2(x-a)]=3(x2-a2). 7.答案为:D. 8.答案为:C;依题意得,f′(x)=-asin x,g′(x)=2x+b,于是有f′(0)=g′(0),即-asin 0=2×0+b,b=0,m=f(0)=g(0),即m=a=1,因此a+b=1. 9.答案为:C;由函数f(x)的图象可得函数f(x)的导函数f′(x)在[0,+∞)上是单调递减的,f(x)在[2,3]上的平均变化率小于函数f(x)在点(2,f(2))处的瞬时变化率,大于f(x)在点(3,f(3))处的瞬时变化率,所以0<f′(3)<<f′(2),即0<f′(3)<f(3)-f(2)<f′(2). 10.答案为:A.11.答案为:C. 12.答案为:C;解析:由f′(x)=g′(x),得f′(x)-g′(x)=0,即[f(x)-g(x)]′=0,所以f(x)-g(x)=C(C为常数). 13.D.14. [答案]D.[解析]由导数的定义容易求得,曲线y=x3-1在x=x0处切线的斜率k1=3x,曲线y=3-0.5x2在x=x0处切线的斜率为k2=-x0,由于两曲线在x=x0处的切线互相垂直,∴3x·(-x0)=-1,故选D. 15.答案为:A;由题意可得点P的坐标为(1,1),f′n(x)=(n+1)·xn,所以fn(x)图象在点P处的切线的斜率为n+1,故可得切线的方程为y-1=(n+1)(x-1),所以切线与x轴交点的横坐标为xn=,则log2 020x1+log2 020x2+…+log2 020x2 019=log2 020(x1x2·…·x2 019)=log2 020=log2 020=-1,故选A. 16. [答案]B;[解析] =2=2 =2f'(x0).17.答案:A;解析:由条件知g′(1)=2,又∵f′(x)=[g(x)+x2]′=g′(x)+2x,∴f′(1)=g′(1)+2=2+2=4. 18.C;∵f '(x)=-![]() cos x+
cos x+![]() (-sin x), f(π)=-
(-sin x), f(π)=-![]() ,∴f(π)+f '
,∴f(π)+f '![]() =-
=-![]() +
+![]() ·(-1)=-
·(-1)=-![]() .19.答案:B;解析:由f(x)=xln x得f′(x)=ln x+1.根据题意知ln x0+1=2,所以ln x0=1,因此x0=e. 20.答案:A;
.19.答案:B;解析:由f(x)=xln x得f′(x)=ln x+1.根据题意知ln x0+1=2,所以ln x0=1,因此x0=e. 20.答案:A; 二 、填空题21.答案为:0.4122.答案为:125/16;
二 、填空题21.答案为:0.4122.答案为:125/16;![]() 23.答案为:y=720x;解析:y'=(x-1)(x-2)…
23.答案为:y=720x;解析:y'=(x-1)(x-2)…![]() (x-6)+x[(x-1)(x-2)…(x-6)]',所以f'(0)=1×2×3×4×5×6+0=720.故切线方程为y=720x.24.答案为:18;
(x-6)+x[(x-1)(x-2)…(x-6)]',所以f'(0)=1×2×3×4×5×6+0=720.故切线方程为y=720x.24.答案为:18;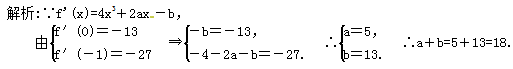 25.答案为:2x-y-2=0;解析:由y=2ln x得y′=.因为k=y′|x=1=2,点(1,0)为切点,所以切线方程为y=2(x-1),即2x-y-2=0. 26.答案为:8; 27.答案为:x+2y-
25.答案为:2x-y-2=0;解析:由y=2ln x得y′=.因为k=y′|x=1=2,点(1,0)为切点,所以切线方程为y=2(x-1),即2x-y-2=0. 26.答案为:8; 27.答案为:x+2y-![]() -
-![]() =0;解析:∵y′=(cos x)′=-sin x,∴k=-sin
=0;解析:∵y′=(cos x)′=-sin x,∴k=-sin![]() =-0.5,∴在点A处的切线方程为x+2y-
=-0.5,∴在点A处的切线方程为x+2y-![]() -
-![]() =0.28.答案为:(0.5,0.25) 29.答案为:-3;
=0.28.答案为:(0.5,0.25) 29.答案为:-3;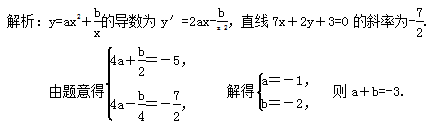 30.答案为:[2,+∞);解析:∵f(x)=x2-ax+ln x的定义域为(0,+∞),∴f′(x)=x-a+.∵f(x)存在垂直于y轴的切线,∴f′(x)存在零点,即x+-a=0有解,∴a=x+≥2(当且仅当x=1时取等号).
30.答案为:[2,+∞);解析:∵f(x)=x2-ax+ln x的定义域为(0,+∞),∴f′(x)=x-a+.∵f(x)存在垂直于y轴的切线,∴f′(x)存在零点,即x+-a=0有解,∴a=x+≥2(当且仅当x=1时取等号).
相关试卷
这是一份高考数学二轮复习题海集训37 函数的最值与导数(30题含答案),共7页。
这是一份高考数学二轮复习题海集训36 函数的极值与导数(30题含答案),共7页。
这是一份高考数学二轮复习题海集训35 函数的单调性与导数(30题含答案),共7页。








