高考数学二轮复习题海集训36 函数的极值与导数（30题含答案）

这是一份高考数学二轮复习题海集训36 函数的极值与导数（30题含答案），共7页。
2020高考数学(理数)题海集训36 函数的极值与导数 一         、选择题1.函数y=f(x)的导数值为0是函数y=f(x)在这点处取得极值的(　　)A.充分不必要条件　　　        B.必要不充分条件C.充要条件                    D.非充分非必要条件 2.对于函数f(x)=x3－3x2，给出命题：①f(x)是增函数，无极值；②f(x)是减函数，无极值；③f(x)的递增区间为(－∞，0)，(2，＋∞)，递减区间为(0,2)；④f(0)=0是极大值，f(2)=－4是极小值.其中正确的命题有(　　)A.1个           B.2个            C.3个              D.4个 3.下列四个函数：①y=x3；②y=x2＋1；③y=|x|；④y=2x，其中在x=0处取得极小值的是(　　)A.①②　　     B.②③　　　   C.③④　　     D.①③ 4.下列函数中，既是奇函数又存在极值的是(　　)A．y=x3　            B．y=ln(－x)         C．y=xe－x                        D．y=x＋ 5.已知y=f(x)是奇函数，当x∈(0，2)时，f(x)=ln x－ax，当x∈(－2，0)时，f(x)的最小值为1，则a=(　　)A.                                    B．              C.                                                  D．1 6.函数f(x)=(x2-1)2＋2的极值点是(　　)A．x=1            B．x=-1        C．x=1或-1或0        D．x=0 7.已知函数f(x)=2x3＋ax2＋36x-24在x=2处有极值，则该函数的一个递增区间是(　　)A.(2,3)           B.(3，＋∞)       C.(2，＋∞)        D.(-∞，3) 8..已知函数y=f(x)，其导函数y=f′(x)的图象如图所示，则y=f(x)(　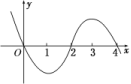　)A.在(-∞，0)上为减函数　              B.在x=0处取极小值C.在(4，＋∞)上为减函数               D.在x=2处取极大值       9.设函数f(x)=ax2＋bx＋c(a，b，c∈R)．若x=－1为函数f(x)ex的一个极值点，则下列图象不可能为y=f(x)图象的是(　　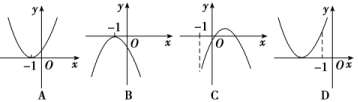) 10.设函数，则(　　)A.x=0.5为f(x)的极大值点         B.x=0.5为f(x)的极小值点C.x=2为f(x)的极大值点           D.x=2为f(x)的极小值点 11.函数f(x)=lnx－x在区间(0，e)上的极大值为(　　)A.－e              B.－1               C.1－e                D.0 12.已知f(x)=x3＋ax2＋(a＋6)x＋1有极大值和极小值，则a的取值范围是(　　)A.(-1,2)                  B.(-3,6)C.(-∞，-3)∪(6，＋∞)       D.(-∞，-1)∪(2，＋∞) 13.已知e为自然对数的底数，设函数f(x)=(ex－1)(x－1)k(k=1，2)，则(　　)A．当k=1时，f(x)在x=1处取得极小值B．当k=1时，f(x)在x=1处取得极大值C．当k=2时，f(x)在x=1处取得极小值D．当k=2时，f(x)在x=1处取得极大值 14.设a∈R，若函数y=ex＋ax(x∈R)有大于零的极值点，则(　　)A.a＜-1         B.a＞-1        C.a＜-      D.a＞- 15.函数f(x)=ax3＋bx在x=1处有极值-2，则a，b的值分别为(　　)A.1，-3　　   B.1,3          C.-1,3        D.-1，-3 16.函数f(x)的定义域为R，导函数f′(x)的图象如图所示，则函数f(x)(　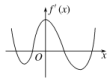　)A.无极大值点，有四个极小值点     B.有三个极大值点，两个极小值点C.有两个极大值点，两个极小值点D.有四个极大值点，无极小值点 17.已知函数f(x)=x3-px2-qx的图象与x轴切于(1,0)点，则f(x)的极大值、极小值分别为(　　)A.，0        B.0，        C.-，0        D.0，-   18.已知函数f(x)的导数f′(x)=a(x＋1)(x-a)，若f(x)在x=a处取到极大值，则a的取值范围是(　　)A.(-∞，-1)　      B.(0，＋∞)         C.(0,1)       D.(-1,0) 19.设函数f(x)的定义域为R，x0(x0≠0)是f(x)的极大值点，以下结论一定正确的是(　　)A．∀x∈R，f(x)≤f(x0)B．－x0是f(－x)的极小值点C．－x0是－f(x)的极小值点D．－x0是－f(－x)的极小值点 20.已知函数f(x)=ex(sin x-cos x)，x∈(0,2 017π)，则函数f(x)的极大值之和为(　　)A.       B.     C.       D. 二         、填空题21.设x=1与x=2是函数f(x)=aln x＋bx2＋x的两个极值点，则常数a=____________. 22.若函数在x=1处取极值，则a=______. 23.已知函数f(x)，x∈R，且在x=1处f(x)存在极小值，则成立的结论为________.(填序号)①当x∈(-∞，1)时，f′(x)>0，当x∈(1，＋∞)时，f′(x)<0；②当x∈(-∞，1)时，f′(x)>0，当x∈(1，＋∞)时，f′(x)>0；③当x∈(-∞，1)时，f′(x)<0，当x∈(1，＋∞)时，f′(x)>0；④当x∈(-∞，1)时，f′(x)<0，当x∈(1，＋∞)时，f′(x)<0. 24.已知函数y=x3＋ax2＋bx＋27在x=-1处有极大值，在x=3处有极小值，则a=______，b=______. 25.不等式ex≥kx对任意实数x恒成立，则实数k的最大值为________． 26.函数f(x)=ax－1－lnx(a≤0)在定义域内的极值点的个数为________. 27.f(x)=x(x－c)2在x=2处有极大值，则常数c的值为________． 28.已知函数f(x)=-k，若x=2是函数f(x)的唯一一个极值点，则实数k的取值范围为________． 29.若函数f(x)=x3＋x2-ax-4在区间(-1,1)上恰有一个极值点，则实数a的取值范围为______. 30.函数f(x)=x3-3bx＋3b在(0,1)内有极小值，则b的取值范围为________.
答案解析1.答案为：B；解析：根据导数的性质可知，若函数y=f(x)在这点处取得极值，则f′(x)=0，即必要性成立；反之不一定成立，如函数f(x)=x3在R上是增函数，f′(x)=3x2，则f′(0)=0，但在x=0处函数不是极值，即充分性不成立.故函数y=f(x)在某点处的导数值为0是函数y=f(x)在这点处取得极值的必要不充分条件，故选B. 2.答案为：B；解析：f′(x)=3x2－6x=3x(x－2)，令f′(x)>0，得x>2或x<0，令f′(x)<0，得0<x<2，∴①②错误，③④正确.3.答案为：B. 4.答案为：D.解析：由题可知，B，C选项中的函数不是奇函数；A选项中，函数y=x3单调递增(无极值)；D选项中的函数既为奇函数又存在极值．  5.答案为：D.解析：因为f(x)是奇函数，所以f(x)在(0，2)上的最大值为－1.当x∈(0，2)时，f′(x)=－a，令f′(x)=0，得x=，又a＞，所以0＜＜2.当x＜时，f′(x)＞0，f(x)在上单调递增；当x＞时，f′(x)＜0，f(x)在上单调递减，所以f(x)max=f=ln －a·=－1，解得a=1.  6.答案为：C；解析：∵f(x)=x4-2x2＋3，∴由f′(x)=4x3-4x=4x(x＋1)(x-1)=0，得x=0或x=1或x=-1，又当x<-1时，f′(x)<0，当-1<x<0时，f′(x)>0，当0<x<1时，f′(x)<0，当x>1时，f′(x)>0，∴x=0,1，-1都是f(x)的极值点．  7.答案为：B.解析：因为函数f(x)=2x3＋ax2＋36x-24在x=2处有极值，又f′(x)=6x2＋2ax＋36，所以f′(2)=0解得a=-15.令f′(x)＞0，解得x＞3或x＜2，所以函数的一个递增区间是(3，＋∞).8.答案为：C.解析：由导函数的图象可知：x∈(-∞，0)∪(2,4)时，f′(x)>0，x∈(0,2)∪(4，＋∞)时，f′(x)<0，因此f(x)在(-∞，0)，(2,4)上为增函数，在(0,2)，(4，＋∞)上为减函数，所以x=0取得极大值，x=2取得极小值，x=4取得极大值，因此选C. 9.答案为：D.解析：因为[f(x)ex]′=f′(x)ex＋f(x)(ex)′=[f(x)＋f′(x)]ex，且x=－1为函数f(x)ex的一个极值点，所以f(－1)＋f′(－1)=0；选项D中，f(－1)＞0，f′(－1)＞0，不满足f′(－1)＋f(－1)=0.  10.答案为：D.解析：由f′(x)=-＋=(1-2x-1)=0可得x=2.当0＜x＜2时，f′(x)＜0，f(x)单调递减；当x＞2时，f′(x)＞0，f(x)单调递增.故x=2为f(x)的极小值点. 11.答案为：B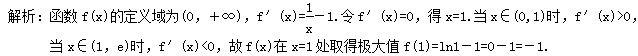；12.答案为：C.解析：f′(x)=3x2＋2ax＋a＋6，∵f(x)有极大值与极小值，∴f′(x)=0有两不等实根，∴Δ=4a2-12(a＋6)>0，∴a<-3或a>6. 13.答案为：C.解析：当k=1时，f′(x)=ex·x－1，f′(1)≠0，∴x=1不是f(x)的极值点．当k=2时，f′(x)=(x－1)(xex＋ex－2)，显然f′(1)=0，且在x=1附近的左侧f′(x)＜0，当x＞1时，f′(x)＞0，∴f(x)在x=1处取得极小值．故选C.  14.答案为：A.解析：∵y=ex＋ax，∴y′=ex＋a.令y′=ex＋a=0，则ex=-a，∴x=ln(-a).又∵x＞0，∴-a＞1，即a＜-1. 15.答案为：A； 16.答案为：C；解析：由导数与函数极值的关系知，当f′(x0)=0时，在x0的左侧f′(x)>0，右侧f′(x)<0，则f(x)在x=x0处取得极大值；若在x0的左侧f′(x)<0，右侧f′(x)>0，则f(x)在x=x0处取得极小值，设y=f′(x)图象与x轴的交点从左到右横坐标依次为x1，x2，x3，x4，则f(x)在x=x1，x=x3处取得极大值，在x=x2，x=x4处取得极小值.17.答案为：A. 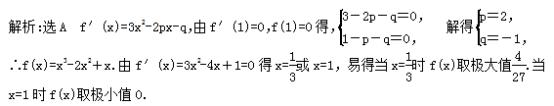18.答案为：D.解析：若a<-1，∵f′(x)=a(x＋1)(x-a)，∴f(x)在(-∞，a)上单调递减，在(a，-1)上单调递增，∴f(x)在x=a处取得极小值，与题意不符；若-1<a<0，则f(x)在(-1，a)上单调递增，在(a，＋∞)上单调递减，从而在x=a处取得极大值.若a>0，则f(x)在(-1，a)上单调递减，在(a，＋∞)上单调递增，与题意矛盾，∴选D. 19.答案为：D.解析：函数f(x)的极大值f(x0)不一定是最大值，故A错误；f(x)与－f(－x)关于原点对称，故x0(x0≠0)是f(x)的极大值点时，－x0是－f(－x)的极小值点，故选D.  20.答案为：B.解析：选B　f′(x)=2exsin x，令f′(x)=0得sin x=0，∴x=kπ，k∈Z，当2kπ<x<2kπ＋π时，f′(x)>0，f(x)单调递增，当(2k-1)π<x<2kπ时，f′(x)<0，f(x)单调递减，∴当x=(2k＋1)π时，f(x)取到极大值，∵x∈(0,2 017π)，∴0<(2k＋1)π<2 017π，∴0≤k<1 008，k∈Z. ∴f(x)的极大值之和为S=f(π)＋f(3π)＋f(5π)＋…＋f(2 015π)=eπ＋e3π＋e5π＋…＋e2 015π==，故选B.  一         、填空题21.答案为：-2/3； 22.答案为：3； 23.答案为：③;解析:∵f(x)在x=1处存在极小值，∴x<1时，f′(x)<0，x>1时，f′(x)>0，故③成立.24.答案为：-3，-9；解析：由题意y′=3x2＋2ax＋b=0的两根为-1和3，∴由根与系数的关系得，-1＋3=-，-1×3=，∴a=-3，b=-9.25.答案为：e；解析：(1)不等式ex≥kx对任意实数x恒成立，即为f(x)=ex－kx≥0恒成立，即有f(x)min≥0，由f(x)的导数为f′(x)=ex－k，当k≤0时，ex＞0，可得f′(x)＞0恒成立，f(x)递增，无最值；当k＞0时，x＞ln k时f′(x)＞0，f(x)递增；x＜ln k时f′(x)＜0，f(x)递减．即在x=ln k处取得最小值，且为k－kln k，由k－kln k≥0，解得k≤e，即k的最大值为e.  26.答案为：0;解析：∵x>0，f′(x)=a－=，∴当a≤0时，f′(x)<0在(0，＋∞)上恒成立，∴函数f(x)在(0，＋∞)上单调递减，∴f(x)在(0，＋∞)上没有极值点.27.答案为：6；解析：f(x)=x3－2cx2＋c2x，f′(x)=3x2－4cx＋c2，f′(2)=0⇒c=2或c=6，若c=2，f′(x)=3x2－8x＋4，令f′(x)＞0⇒x＜或x＞2，f′(x)＜0⇒＜x＜2，故函数在及(2，＋∞)上单调递增，在上单调递减，所以x=2是极小值点，故c=2(不合题意，舍去)，c=6.  28.答案为：(-∞，e]；解析：f′(x)=-k=(x>0)．设g(x)=(x>0)，则g′(x)=，∴g(x)在(0,1)上单调递减，在(1，＋∞)上单调递增．∴g(x)在(0，＋∞)上有最小值，为g(1)=e，结合g(x)=与y=k的图象可知，要满足题意，只需k≤e.  29.答案为：[1,5)；解析：由题意，f′(x)=3x2＋2x-a，则f′(-1)f′(1)<0，即(1-a)(5-a)<0，解得1<a<5，另外，当a=1时，函数f(x)=x3＋x2-x-4在区间(-1，1)上恰有一个极值点，当a=5时，函数f(x)=x3＋x2-5x-4在区间(-1,1)没有极值点.故实数a的范围为[1,5). 30.答案为：(0,1)；