


所属成套资源:高考数学二轮复习题海集训 (30题含答案)
高考数学二轮复习题海集训38 分类加法计数原理与分步乘法计数原理(30题含答案)
展开
这是一份高考数学二轮复习题海集训38 分类加法计数原理与分步乘法计数原理(30题含答案),共7页。
2020高考数学(理数)题海集训38 分类加法计数原理与分步乘法计数原理 一 、选择题1.从甲地到乙地一天有汽车8班,火车3班,轮船2班,某人从甲地到乙地,他共有不同的走法数为( )A.13种 B.16种 C.24种 D.48种 2.如图,一环形花坛分成A,B,C,D四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为( )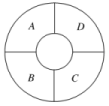 A.96 B.84 C.60 D.48 3.从个位数与十位数之和为奇数的两位数中任取一个,其个位数为0的概率是( )A. B. C. D. 4. (a1+a2+a3+a4)·(b1+b2)·(c1+c2+c3)展开后共有不同的项数为( )A.9 B.12 C.18 D.24 5.如下图所示,小圆圈表示网络的结点,结点之间的线段表示它们有网线相连.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开从不同的路线同时传递,则单位时间内传递的最大信息量为( )
A.96 B.84 C.60 D.48 3.从个位数与十位数之和为奇数的两位数中任取一个,其个位数为0的概率是( )A. B. C. D. 4. (a1+a2+a3+a4)·(b1+b2)·(c1+c2+c3)展开后共有不同的项数为( )A.9 B.12 C.18 D.24 5.如下图所示,小圆圈表示网络的结点,结点之间的线段表示它们有网线相连.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开从不同的路线同时传递,则单位时间内传递的最大信息量为( )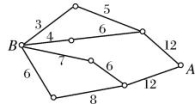 A.26 B.24 C.20 D.19 6.12名同学合影,站成了前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是 ( )A.CA B.CA C.CA D.CA 7.已知x∈{2,3,7},y∈{-3,-4,8},则x·y可表示不同的值的个数为( )A.8个 B.12个 C.10个 D.9个 8.有四位老师在同一年级的4个班级中,各教一个班的数学,在数学考试时,要求每位老师均不在本班监考,则安排监考的方法种数是( )A.8种 B.9种 C.10种 D.11种 9.从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a,b组成复数a+bi,其中虚数的个数是( )A.30 B.42 C.36 D.35 10.用0、1、…、9十个数字,可以组成有重复数字的三位数的个数为( )A.243 B.252 C.261 D.279 11.已知两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为( )A.40 B.16 C.13 D.10 12.体育老师把9个相同的足球放入编号为1,2,3的三个箱子中,要求每个箱子放球的个数不小于其编号,则不同的放球方法有( )A.8种 B.10种 C.12种 D.16种 13.有5个不同的棱柱、3个不同的棱锥、4个不同的圆台、2个不同的球,若从中取出2个几何体,使多面体和旋转体各一个,则不同的取法种数是( )A.14 B.23 C.48 D.120 14.从0、2中选一个数字,从1、3、5中选两个数字,组成无重复数字的三位数,其中奇数的个数为( )A.24 B.18 C.12 D.6 15.下图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,现在用四种颜色给这四个直角三角形区域涂色,规定每个区域只涂一个颜色,相邻区域颜色不相同,则不同的涂色方法有( )
A.26 B.24 C.20 D.19 6.12名同学合影,站成了前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是 ( )A.CA B.CA C.CA D.CA 7.已知x∈{2,3,7},y∈{-3,-4,8},则x·y可表示不同的值的个数为( )A.8个 B.12个 C.10个 D.9个 8.有四位老师在同一年级的4个班级中,各教一个班的数学,在数学考试时,要求每位老师均不在本班监考,则安排监考的方法种数是( )A.8种 B.9种 C.10种 D.11种 9.从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a,b组成复数a+bi,其中虚数的个数是( )A.30 B.42 C.36 D.35 10.用0、1、…、9十个数字,可以组成有重复数字的三位数的个数为( )A.243 B.252 C.261 D.279 11.已知两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为( )A.40 B.16 C.13 D.10 12.体育老师把9个相同的足球放入编号为1,2,3的三个箱子中,要求每个箱子放球的个数不小于其编号,则不同的放球方法有( )A.8种 B.10种 C.12种 D.16种 13.有5个不同的棱柱、3个不同的棱锥、4个不同的圆台、2个不同的球,若从中取出2个几何体,使多面体和旋转体各一个,则不同的取法种数是( )A.14 B.23 C.48 D.120 14.从0、2中选一个数字,从1、3、5中选两个数字,组成无重复数字的三位数,其中奇数的个数为( )A.24 B.18 C.12 D.6 15.下图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,现在用四种颜色给这四个直角三角形区域涂色,规定每个区域只涂一个颜色,相邻区域颜色不相同,则不同的涂色方法有( ) A.24种 B.72种 C.84种 D.120种16.从集合{1,2,3,4,5}中任取2个不同的数,作为方程Ax+By=0的系数A、B的值,则形成的不同直线有( )A.18条 B.20条 C.25条 D.10条 17.从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列的个数为( )A.3 B.4 C.6 D.8 18.甲与其四位同事各有一辆私家车,车牌尾数分别是0,0,2,1,5,为遵守当地某月5日至9日5天的限行规定(奇数日车牌尾数为奇数的车通行,偶数日车牌尾数为偶数的车通行),五人商议拼车出行,每天任选一辆符合规定的车,但甲的车最多只能用一天,则不同的用车方案种数为( )A.5 B.24 C.32 D.64 19.满足a,b∈{-1,0,1,2},且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为( )A.14 B.13 C.12 D.10 20.5本不同的书全部分给4个学生,每个学生至少1本,不同的分法种数有( )A.480 B.240 C.120 D.96 二 、填空题21.直线方程Ax+By=0,若从0,1,3,5,7,8这6个数字中每次取两个不同的数作为A,B的值,则可表示 条不同的直线. 22.在连接正八边形的顶点而成的三角形中,与正八边形有公共边的三角形有 个. 23.从2,3,5,7,11中每次选出两个不同的数作为分数的分子、分母,则可产生不同的分数的个数是________,其中真分数的个数是________. 24.现有五种不同的颜色,要对图形中的四个部分进行着色,要求有公共边的两块不能用同一种颜色,不同的涂色方法有 种.
A.24种 B.72种 C.84种 D.120种16.从集合{1,2,3,4,5}中任取2个不同的数,作为方程Ax+By=0的系数A、B的值,则形成的不同直线有( )A.18条 B.20条 C.25条 D.10条 17.从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列的个数为( )A.3 B.4 C.6 D.8 18.甲与其四位同事各有一辆私家车,车牌尾数分别是0,0,2,1,5,为遵守当地某月5日至9日5天的限行规定(奇数日车牌尾数为奇数的车通行,偶数日车牌尾数为偶数的车通行),五人商议拼车出行,每天任选一辆符合规定的车,但甲的车最多只能用一天,则不同的用车方案种数为( )A.5 B.24 C.32 D.64 19.满足a,b∈{-1,0,1,2},且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为( )A.14 B.13 C.12 D.10 20.5本不同的书全部分给4个学生,每个学生至少1本,不同的分法种数有( )A.480 B.240 C.120 D.96 二 、填空题21.直线方程Ax+By=0,若从0,1,3,5,7,8这6个数字中每次取两个不同的数作为A,B的值,则可表示 条不同的直线. 22.在连接正八边形的顶点而成的三角形中,与正八边形有公共边的三角形有 个. 23.从2,3,5,7,11中每次选出两个不同的数作为分数的分子、分母,则可产生不同的分数的个数是________,其中真分数的个数是________. 24.现有五种不同的颜色,要对图形中的四个部分进行着色,要求有公共边的两块不能用同一种颜色,不同的涂色方法有 种.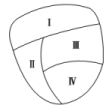 25.按ABO血型系统学说,每个人的血型为A,B,O,AB四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB型时,子女一定不是O型,若某人的血型为O型,则父母血型所有可能情况有________种. 26.已知△ABC三边a,b,c的长都是整数,且a≤b≤c,如果b=25,则符合条件的三角形共有 个. 27.从数字1,2,3,4,5,6中取两个数相加,共得 个不同的偶数. 28.5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛 ,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有 种.(用数字作答) 29.将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有________种(用数字作答) 30.从集合{1,2,3,4,5,6}中任取两个元素作为双曲线-=1中的几何量a、b的值,则“双曲线渐近线的斜率k满足|k|≤1”的概率为 .
25.按ABO血型系统学说,每个人的血型为A,B,O,AB四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB型时,子女一定不是O型,若某人的血型为O型,则父母血型所有可能情况有________种. 26.已知△ABC三边a,b,c的长都是整数,且a≤b≤c,如果b=25,则符合条件的三角形共有 个. 27.从数字1,2,3,4,5,6中取两个数相加,共得 个不同的偶数. 28.5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛 ,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有 种.(用数字作答) 29.将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有________种(用数字作答) 30.从集合{1,2,3,4,5,6}中任取两个元素作为双曲线-=1中的几何量a、b的值,则“双曲线渐近线的斜率k满足|k|≤1”的概率为 .
答案解析1.A.[解析] 应用分类加法计数原理,不同走法数为8+3+2=13(种).故选A. 2.B.解析:A有4种选择,B有3种选择,若C与A相同,则D有3种选择,若C与A不同,则C有2种选择,D也有2种选择,所以共有4×3×(3+2×2)=84种. 3.D.[解析]本题考查计数原理与古典概型,∵两数之和为奇数,则两数一奇一偶,若个位数为奇数,则共有4×5=20个数,若个位数为偶数,共有5×5=25个数,其中个位为0的数共有5个,∴P==. 4.D.解析:由分步乘法计数原理得共有不同的项数为4×2×3=24.故选D. 5.D.[解析] 因信息可以分开沿不同的路线同时传递,由分类加法计数原理,完成从A向B传递有四种方法:12→5→3,12→6→4,12→6→7,12→8→6,故单位时间内传递的最大信息量为四条不同网线上信息量的和:3+4+6+6=19,故选D. 6.C.解析:从后排8人中选2人安排到前排6个位置中的任意两个位置即可,所以选法种数是CA,故选C. 7.D.解析:分两步:第一步,在集合{2,3,7}中任取一个值,有3种不同的取法;第二步,在集合{-3,-4,8}中任取一个值,有3种不同取法.故x·y可表示3×3=9(个)不同的值.故选D. 8.B.[解析]设四个班级分别是A、B、C、D,它们的老师分别是a、b、c、d,并设a监考的是B,则剩下的三个老师分别监考剩下的三个班级,共有3种不同的方法;同理当a监考C、D时,剩下的三个老师分别监考剩下的三个班级也各有3种不同的方法.这样,由分类加法计数原理知共有3+3+3=9(种)不同的安排方法.另外,本题还可让a先选,可从B、C、D中选一个,即有3种选法.若选的是B,则b从剩下的3个班级中任选一个,也有3种选法,剩下的两个老师都只有一种选法,这样用分步乘法计数原理求解,共有3×3×1×1=9(种)不同的安排方法. 9.答案为:C.解析:因为a+bi为虚数,所以b≠0,即b有6种取法,a有6种取法,由分步乘法计数原理知可以组成6×6=36个虚数. 10.B.[解析]用0,1,…,9十个数字,可以组成的三位数的个数为9×10×10=900,其中三位数字全不相同的为9×9×8=648,所以可以组成有重复数字的三位数的个数为900-648=252. 11.C.解析:分两类:第1类,直线a与直线b上8个点可以确定8个不同的平面;第2类,直线b与直线a上5个点可以确定5个不同的平面.故可以确定8+5=13个不同的平面. 12.B.[解析]首先在三个箱子中放入个数与编号相同的球,这样剩下三个足球,这三个足球可以随意放置,第一种方法,可以在每一个箱子中放一个,有1种结果;第二种方法,可以把球分成两份,1和2,这两份在三个位置,有3×2=6种结果;第三种方法,可以把三个球都放到一个箱子中,有3种结果.综上可知共有1+6+3=10种结果. 13.C.解析:分两步:第一步,取多面体,有5+3=8种不同的取法,第二步,取旋转体,有4+2=6种不同的取法.所以不同的取法种数是8×6=48种. 14.B.[解析](1)当从0,2中选取2时,组成的三位奇数的个位只能奇数,只要2不排在个位即可,先排2再排1,3,5中选出的两个奇数,共有2×3×2=12(个).(2)当从0,2中选取0时,组成的三位奇数的个位只能是奇数,0必须在十位,只要排好从1,3,5中选出的两个奇数.共有3×2=6(个).综上,由分类加法计数原理知共有12+6=18(个). 15.答案为:C;解析:如图,设四个直角三角形依次为A,B,C,D,下面分两种情况:  (1)A,C不同色(注意:B,D可同色、也可不同色,D只要不与A,C同色即可,所以D可以从剩余的2种颜色中任意取一色):有4×3×2×2=48(种)涂色方法.(2)A,C同色(注意:B,D可同色、也可不同色,D只要不与A,C同色即可,所以D可以从剩余的3种颜色中任意取一色):有4×3×1×3=36(种)涂色方法,综上,共有48+36=84种涂色方法.故选C.16.A.解析:第一步,取A的值,有5种取法;第二步,取B的值,有4种取法,其中当A=1,B=2时与A=2,B=4时是相同的方程;当A=2,B=1时与A=4,B=2时是相同的方程,故共有5×4-2=18条. 17.D.[解析] 当公比为2时,等比数列可为1、2、4,2、4、8.当公比为3时,等比数列可为1、3、9.当公比为时,等比数列可为4、6、9.同时,4、2、1,8、4、2,9、3、1和9、6、4也是等比数列,共8个. 18.D.解析:5日至9日,有3天奇数日,2天偶数日,第一步安排奇数日出行,每天都有2种选择,共有23=8(种),第二步安排偶数日出行分两类,第一类,先选1天安排甲的车,另外一天安排其他车,有2×2=4(种).第二类,不安排甲的车,每天都有2种选择,共有22=4(种),共计4+4=8,根据分步乘法计数原理,不同的用车方案种数共有8×8=64.故选D. 19.B.解析:当a=0时,关于x的方程为2x+b=0,此时有序数对(0,-1),(0,0),(0,1),(0,2)均满足要求;当a≠0时,Δ=4-4ab≥0,ab≤1,此时满足要求的有序数对为(-1,-1),(-1,0),(-1,1),(-1,2),(1,-1),(1,0),(1,1),(2,-1),(2,0).综上,满足要求的有序数对共有13个,选B. 20.B.解析:先把5本书中的两本捆起来,再分成4份即可,∴分法种数为CA=240. 一 、填空题21.答案为:22;[解析]若A或B中有一个为零时,有2条;当AB≠0时有5×4=20条,故共有20+2=22条不同的直线. 22.答案为:40;解析:分两类:①有一条公共边的三角形共有8×4=32个;②有两条公共边的三角形共有8个.故共有32+8=40个.23.答案为:20,10.解析:产生分数可分两步:第一步,产生分子有5种方法;第二步,产生分母有4种方法,共有5×4=20个分数.产生真分数,可分四类:第一类,当分子是2时,有4个真分数,同理,当分子分别是3,5,7时,真分数的个数分别是3,2,1,共有4+3+2+1=10个真分数. 24.答案为:180;[解析]依次给区域Ⅰ、Ⅱ、Ⅲ、Ⅳ涂色分别有5、4、3、3种方法,根据分步乘法计数原理,不同的涂色方法的种数为5×4×3×3=180. 25.答案为:9;解析:父母应为A或B或O,C·C=9(种). 26.答案为:325;解析:根据三角形的三边关系可知,c<25+a.第一类,当a=1,b=25时,c可取25,共1个;第二类,当a=2,b=25时,c可取25,26,共2个;……当a=25,b=25时,c可取25,26,…,49,共25个.所以符合条件的三角形的个数为1+2+…+25=325.27.答案为:4.[解析]由两个数相加是偶数知两个数都是偶数或两个数都是奇数,分两类,第一类,两个数都是偶数,2+4=6,2+6=8,4+6=10,共得3个偶数,第二类,两个数都是奇数,1+3=4,1+5=6,3+5=8,共得3个偶数,∵2+6=3+5,2+4=1+5,∴从数字1,2,3,4,5,6中取两个相加,共得4个不同的偶数, 28.答案为:48;[解析]本题可分为两类完成:两老一新时,有3×2×2=12(种)排法;两新一老时,有2×3×3×2=36(种)排法,即共有48种排法. 29.答案为:480.解析:按C的位置分类计算.①当C在第一或第六位时,有A=120(种)排法;②当C在第二或第五位时,有AA=72(种)排法;③当C在第三或第四位时,有AA+AA=48(种)排法.所以共有2×(120+72+48)=480(种)排法. 30.答案为:;[解析]所有可能取法有6×5=30种,由|k|=≤1知b≤a,满足此条件的有(2,1),(3,2),(3,1),(4,3),(4,2),(4,1),(5,4),(5,3),(5,2),(5,1),(6,5),(6,4),(6,3),(6,2),(6,1)共15种,∴所求概率P==.
(1)A,C不同色(注意:B,D可同色、也可不同色,D只要不与A,C同色即可,所以D可以从剩余的2种颜色中任意取一色):有4×3×2×2=48(种)涂色方法.(2)A,C同色(注意:B,D可同色、也可不同色,D只要不与A,C同色即可,所以D可以从剩余的3种颜色中任意取一色):有4×3×1×3=36(种)涂色方法,综上,共有48+36=84种涂色方法.故选C.16.A.解析:第一步,取A的值,有5种取法;第二步,取B的值,有4种取法,其中当A=1,B=2时与A=2,B=4时是相同的方程;当A=2,B=1时与A=4,B=2时是相同的方程,故共有5×4-2=18条. 17.D.[解析] 当公比为2时,等比数列可为1、2、4,2、4、8.当公比为3时,等比数列可为1、3、9.当公比为时,等比数列可为4、6、9.同时,4、2、1,8、4、2,9、3、1和9、6、4也是等比数列,共8个. 18.D.解析:5日至9日,有3天奇数日,2天偶数日,第一步安排奇数日出行,每天都有2种选择,共有23=8(种),第二步安排偶数日出行分两类,第一类,先选1天安排甲的车,另外一天安排其他车,有2×2=4(种).第二类,不安排甲的车,每天都有2种选择,共有22=4(种),共计4+4=8,根据分步乘法计数原理,不同的用车方案种数共有8×8=64.故选D. 19.B.解析:当a=0时,关于x的方程为2x+b=0,此时有序数对(0,-1),(0,0),(0,1),(0,2)均满足要求;当a≠0时,Δ=4-4ab≥0,ab≤1,此时满足要求的有序数对为(-1,-1),(-1,0),(-1,1),(-1,2),(1,-1),(1,0),(1,1),(2,-1),(2,0).综上,满足要求的有序数对共有13个,选B. 20.B.解析:先把5本书中的两本捆起来,再分成4份即可,∴分法种数为CA=240. 一 、填空题21.答案为:22;[解析]若A或B中有一个为零时,有2条;当AB≠0时有5×4=20条,故共有20+2=22条不同的直线. 22.答案为:40;解析:分两类:①有一条公共边的三角形共有8×4=32个;②有两条公共边的三角形共有8个.故共有32+8=40个.23.答案为:20,10.解析:产生分数可分两步:第一步,产生分子有5种方法;第二步,产生分母有4种方法,共有5×4=20个分数.产生真分数,可分四类:第一类,当分子是2时,有4个真分数,同理,当分子分别是3,5,7时,真分数的个数分别是3,2,1,共有4+3+2+1=10个真分数. 24.答案为:180;[解析]依次给区域Ⅰ、Ⅱ、Ⅲ、Ⅳ涂色分别有5、4、3、3种方法,根据分步乘法计数原理,不同的涂色方法的种数为5×4×3×3=180. 25.答案为:9;解析:父母应为A或B或O,C·C=9(种). 26.答案为:325;解析:根据三角形的三边关系可知,c<25+a.第一类,当a=1,b=25时,c可取25,共1个;第二类,当a=2,b=25时,c可取25,26,共2个;……当a=25,b=25时,c可取25,26,…,49,共25个.所以符合条件的三角形的个数为1+2+…+25=325.27.答案为:4.[解析]由两个数相加是偶数知两个数都是偶数或两个数都是奇数,分两类,第一类,两个数都是偶数,2+4=6,2+6=8,4+6=10,共得3个偶数,第二类,两个数都是奇数,1+3=4,1+5=6,3+5=8,共得3个偶数,∵2+6=3+5,2+4=1+5,∴从数字1,2,3,4,5,6中取两个相加,共得4个不同的偶数, 28.答案为:48;[解析]本题可分为两类完成:两老一新时,有3×2×2=12(种)排法;两新一老时,有2×3×3×2=36(种)排法,即共有48种排法. 29.答案为:480.解析:按C的位置分类计算.①当C在第一或第六位时,有A=120(种)排法;②当C在第二或第五位时,有AA=72(种)排法;③当C在第三或第四位时,有AA+AA=48(种)排法.所以共有2×(120+72+48)=480(种)排法. 30.答案为:;[解析]所有可能取法有6×5=30种,由|k|=≤1知b≤a,满足此条件的有(2,1),(3,2),(3,1),(4,3),(4,2),(4,1),(5,4),(5,3),(5,2),(5,1),(6,5),(6,4),(6,3),(6,2),(6,1)共15种,∴所求概率P==.
相关试卷
这是一份课时跟踪检测(一) 分类加法计数原理与分步乘法计数原理,共4页。
这是一份高中数学人教A版 (2019)选择性必修 第三册6.1 分类加法计数原理与分步乘法计数原理同步达标检测题,共22页。试卷主要包含了分类加法计数原理与集合类比等内容,欢迎下载使用。
这是一份数学选修2-31.1分类加法计数原理与分步乘法计.课时作业,共3页。








