


所属成套资源:高考数学二轮复习题海集训 (30题含答案)
高考数学二轮复习题海集训40 二项式定理(30题含答案)
展开
这是一份高考数学二轮复习题海集训40 二项式定理(30题含答案),共7页。试卷主要包含了在原二项展开式中令x=1,,令eq \f=0,,5;等内容,欢迎下载使用。
2020高考数学(理数)题海集训40 二项式定理 一 、选择题1.在(1+x)n(x∈N*)的二项展开式中,若只有x5的系数最大,则n=( )A.8 B.9 C.10 D.11 2.在x(1+x)6的展开式中,含x3项的系数为( ) A.30 B.20 C.15 D.10 3.5的展开式中x2y3的系数是( )A.-20 B.-5 C.5 D.20 4.若(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a0|-|a1|+|a2|-|a3|+|a4|-|a5|=( )A.0 B.1 C.32 D.-1 5. (x-y)(x+2y+z)6的展开式中,x2y3z2的系数为( )A.-30 B.120 C.240 D.420 6.设n为正整数,2n展开式中存在常数项,则n的一个可能取值为( )A.16 B.10 C.4 D.2 7.设复数x=(i是虚数单位),则Cx+Cx2+Cx3+…+Cx2 020=( )A.i B.-i C.0 D.-1-i 8.6的展开式中常数项为( )A.2.5 B.160 C.-2.5 D.-160 9. (1-3x)7的展开式的第4项的系数为( )A.-27C B.-81C C.27C D.81C 10.二项式10的展开式中的常数项是( )A.180 B.90 C.45 D.360 11.若二项式n展开式中的第5项是常数,则自然数n的值为( )A.6 B.10 C.12 D.15 12.6的展开式中,常数项是( )A.- B. C.- D. 13.5的展开式中常数项为( )A.-30 B.30 C.-25 D.25 14.已知(3x-1)n=a0+a1x+a2x2+a3x3+…+anxn(n∈N*),设(3x-1)n展开式的二项式系数和为Sn,Tn=a1+a2+a3+…+an(n∈N*),Sn与Tn的大小关系是( )A.Sn>TnB.Sn<TnC.n为奇数时,Sn<Tn,n为偶数时,Sn>TnD.Sn=Tn 15.若n的展开式中所有项系数的绝对值之和为1 024,则该展开式中的常数项为( )A.-270 B.270 C.-90 D.90 16.若(x-2y)6的展开式中的二项式系数和为S,x2y4的系数为P,则为( )A. B. C.120 D.240 17. (x+y+z)4的展开式的项数为( )A.10 B.15 C.20 D.21 18.在(x-2)6展开式中,二项式系数的最大值为m,含x5项的系数为n,则=( )A. B.- C. D.- 19.5的展开式中常数项为( )A.-30 B.30 C.-25 D.25 20.在二项式n的展开式中,各项系数之和为A,各项二项式系数之和为B,且A+B=72,则展开式中常数项的值为( )A.6 B.9 C.12 D.18 二 、填空题21.![]() 的展开式中的常数项为 . 22.5的展开式中各项系数的和为2,则该展开式中含x4项的系数为________. 23.若(x-1)5=a5(x+1)5+a4(x+1)4+a3(x+1)3+a2(x+1)2+a1(x+1)+a0,则a1+a2+a3+a4+a5=________. 24.若(2+x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a3= (用数字作答). 25.在多项式(1+2x)6(1+y)5的展开式中,xy3的系数为________. 26.在二项式5的展开式中,若常数项为-10,则a=________. 27.9的展开式中x3的系数为-84,则展开式的各项系数之和为________. 28.若n(n≥4,n∈N*)的二项展开式中前三项的系数依次成等差数列,则n=________. 29.已知(1-2x)5(1+ax)4的展开式中x的系数为2,则实数a的值为________. 30.若
的展开式中的常数项为 . 22.5的展开式中各项系数的和为2,则该展开式中含x4项的系数为________. 23.若(x-1)5=a5(x+1)5+a4(x+1)4+a3(x+1)3+a2(x+1)2+a1(x+1)+a0,则a1+a2+a3+a4+a5=________. 24.若(2+x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a3= (用数字作答). 25.在多项式(1+2x)6(1+y)5的展开式中,xy3的系数为________. 26.在二项式5的展开式中,若常数项为-10,则a=________. 27.9的展开式中x3的系数为-84,则展开式的各项系数之和为________. 28.若n(n≥4,n∈N*)的二项展开式中前三项的系数依次成等差数列,则n=________. 29.已知(1-2x)5(1+ax)4的展开式中x的系数为2,则实数a的值为________. 30.若![]() ,则
,则![]() 的展开式中常数项为 .
的展开式中常数项为 .
0.2020高考数学(理数)题海集训40 二项式定理1.答案为:C;解析:二项式中仅x5项系数最大,其最大值必为Cn,即得=5,解得n=10.2.答案为:C;![]() 3.答案为:A;解析:由二项展开式的通项可得,第四项T4=C2(-2y)3=-20x2y3,故x2y3的系数为-20,选A. 4.答案为:A;解析:由(1-x)5的展开式的通项Tr+1=C(-x)r=C(-1)rxr,可知a1,a3,a5都小于0.则|a0|-|a1|+|a2|-|a3|+|a4|-|a5|=a0+a1+a2+a3+a4+a5.在原二项展开式中令x=1,可得a0+a1+a2+a3+a4+a5=0.故选A. 5.答案为:B;解析:[(x+2y)+z]6的展开式中含z2的项为C(x+2y)4z2,(x+2y)4的展开式中xy3项的系数为C×23,x2y2项的系数为C×22,∴(x-y)(x+2y+z)6的展开式中x2y3z2的系数为CC×23-CC×22=480-360=120,故选B. 6.答案为:B.解析:2n展开式的通项公式为Tk+1=Cx2n-kk=C(-1)kx.令=0,得k=,又k为正整数,所以n可取10. 7.答案为:C.解析:x==-1+i,Cx+Cx2+Cx3+…+Cx2 020=(1+x)2 020-1=i2 020-1=0. 8.答案为:A.解析:6的展开式的通项Tr+1=Cx6-rr=rCx6-2r,令6-2r=0,得r=3,所以展开式中的常数项是T4=3C=,选A. 9.答案为:A;解析:(1-3x)7的展开式的第4项为T3+1=C×17-3×(-3x)3=-27Cx3,其系数为-27C,选A. 10.答案为:A;解析:10的展开式的通项为Tk+1=C·()10-kk=2kC
3.答案为:A;解析:由二项展开式的通项可得,第四项T4=C2(-2y)3=-20x2y3,故x2y3的系数为-20,选A. 4.答案为:A;解析:由(1-x)5的展开式的通项Tr+1=C(-x)r=C(-1)rxr,可知a1,a3,a5都小于0.则|a0|-|a1|+|a2|-|a3|+|a4|-|a5|=a0+a1+a2+a3+a4+a5.在原二项展开式中令x=1,可得a0+a1+a2+a3+a4+a5=0.故选A. 5.答案为:B;解析:[(x+2y)+z]6的展开式中含z2的项为C(x+2y)4z2,(x+2y)4的展开式中xy3项的系数为C×23,x2y2项的系数为C×22,∴(x-y)(x+2y+z)6的展开式中x2y3z2的系数为CC×23-CC×22=480-360=120,故选B. 6.答案为:B.解析:2n展开式的通项公式为Tk+1=Cx2n-kk=C(-1)kx.令=0,得k=,又k为正整数,所以n可取10. 7.答案为:C.解析:x==-1+i,Cx+Cx2+Cx3+…+Cx2 020=(1+x)2 020-1=i2 020-1=0. 8.答案为:A.解析:6的展开式的通项Tr+1=Cx6-rr=rCx6-2r,令6-2r=0,得r=3,所以展开式中的常数项是T4=3C=,选A. 9.答案为:A;解析:(1-3x)7的展开式的第4项为T3+1=C×17-3×(-3x)3=-27Cx3,其系数为-27C,选A. 10.答案为:A;解析:10的展开式的通项为Tk+1=C·()10-kk=2kC![]() ,令5-k=0,得k=2,故常数项为22C=180. 11.答案为:C;解析:由二项式n展开式的第5项C()n-44=
,令5-k=0,得k=2,故常数项为22C=180. 11.答案为:C;解析:由二项式n展开式的第5项C()n-44=![]() 是常数项,可得-6=0,解得n=12. 12.答案为:D.解析:Tr+1=C(x2)6-rr=rCx12-3r,令12-3r=0,解得r=4.所以常数项为4C=.故选D. 13.答案为:C;解析:5=x25-3x5+5,5的展开式的通项Tr+1=C(-1)rr,易知当r=4或r=2时原式有常数项,令r=4,T5=C(-1)44,令r=2,T3=C(-1)2·2,故所求常数项为C-3×C=5-30=-25,故选C. 14.答案为:C;解析:Sn=2n,令x=1,得a0+a1+a2+…+an=2n,令x=0,得a0=(-1)n,所以Tn=a1+a2+a3+…+an=Sn-a0=Sn-(-1)n,所以当n为偶数时,Tn=Sn-1<Sn,当n为奇数时,Tn=Sn+1>Sn,故选C. 15.答案为:C;解析:n的展开式中所有项系数的绝对值之和等于n的展开式中所有项系数之和.令x=1,得4n=1 024,∴n=5.则n=5,其通项Tr+1=C5-r·(-)r=C·35-r·(-1)r·
是常数项,可得-6=0,解得n=12. 12.答案为:D.解析:Tr+1=C(x2)6-rr=rCx12-3r,令12-3r=0,解得r=4.所以常数项为4C=.故选D. 13.答案为:C;解析:5=x25-3x5+5,5的展开式的通项Tr+1=C(-1)rr,易知当r=4或r=2时原式有常数项,令r=4,T5=C(-1)44,令r=2,T3=C(-1)2·2,故所求常数项为C-3×C=5-30=-25,故选C. 14.答案为:C;解析:Sn=2n,令x=1,得a0+a1+a2+…+an=2n,令x=0,得a0=(-1)n,所以Tn=a1+a2+a3+…+an=Sn-a0=Sn-(-1)n,所以当n为偶数时,Tn=Sn-1<Sn,当n为奇数时,Tn=Sn+1>Sn,故选C. 15.答案为:C;解析:n的展开式中所有项系数的绝对值之和等于n的展开式中所有项系数之和.令x=1,得4n=1 024,∴n=5.则n=5,其通项Tr+1=C5-r·(-)r=C·35-r·(-1)r·![]() ,令+=0,解得r=3,∴该展开式中的常数项为T4=C·32·(-1)3=-90,故选C. 16.答案为:B;解析:由题意知,S=C+C+…+C=26=64,P=C(-2)4=15×16=240,故==.故选B. 17.答案为:B.解析:(x+y+z)4=[(x+y)+z]4=C(x+y)4+C(x+y)3z+C(x+y)2z2+C(x+y)z3+Cz4,运用二项式定理展开共有5+4+3+2+1=15项,选B. 18.答案为:D;解析:因为n=6是偶数,所以展开式共有7项,其中中间一项的二项式系数最大,其二项式系数为m=C=20,含x5项的系数为n=(-1)C×2=-12,则=-=-.故选D. 19.答案为:C.解析:5=x25-3x5+5,5的展开式的通项Tr+1=C(-1)rr,易知当r=4或r=2时原式有常数项,令r=4,T5=C(-1)44,令r=2,T3=C(-1)22,故所求常数项为C-3×C=5-30=-25,故选C. 20.答案为:B;解析:在二项式n的展开式中,令x=1得各项系数之和为4n,即A=4n,二项展开式中二项式系数之和为2n,即B=2n.∵A+B=72,∴4n+2n=72,解得n=3,∴n=3的展开式的通项为Tr+1=C()3-rr=3rCx,令=0,得r=1,故展开式中常数项为T2=3×C=9,故选B. 21.答案为:4 246;
,令+=0,解得r=3,∴该展开式中的常数项为T4=C·32·(-1)3=-90,故选C. 16.答案为:B;解析:由题意知,S=C+C+…+C=26=64,P=C(-2)4=15×16=240,故==.故选B. 17.答案为:B.解析:(x+y+z)4=[(x+y)+z]4=C(x+y)4+C(x+y)3z+C(x+y)2z2+C(x+y)z3+Cz4,运用二项式定理展开共有5+4+3+2+1=15项,选B. 18.答案为:D;解析:因为n=6是偶数,所以展开式共有7项,其中中间一项的二项式系数最大,其二项式系数为m=C=20,含x5项的系数为n=(-1)C×2=-12,则=-=-.故选D. 19.答案为:C.解析:5=x25-3x5+5,5的展开式的通项Tr+1=C(-1)rr,易知当r=4或r=2时原式有常数项,令r=4,T5=C(-1)44,令r=2,T3=C(-1)22,故所求常数项为C-3×C=5-30=-25,故选C. 20.答案为:B;解析:在二项式n的展开式中,令x=1得各项系数之和为4n,即A=4n,二项展开式中二项式系数之和为2n,即B=2n.∵A+B=72,∴4n+2n=72,解得n=3,∴n=3的展开式的通项为Tr+1=C()3-rr=3rCx,令=0,得r=1,故展开式中常数项为T2=3×C=9,故选B. 21.答案为:4 246; 22.答案为:-48;解析:因为展开式中各项系数的和为2,所以令x=1,得(1-a)×1=2,解得a=-1.5展开式的通项公式为Tr+1=C(2x)5-rr=(-1)r25-rCx5-2r,令5-2r=3,得r=1,展开式中含x3项的系数为T2=(-1)×24C=-80,令5-2r=5,得r=0,展开式中含x5项的系数为T1=25C=32,所以5的展开式中含x4项的系数为-80+32=-48. 23.答案为:31;解析:令x=-1可得a0=-32.令x=0可得a0+a1+a2+a3+a4+a5=-1,所以a1+a2+a3+a4+a5=-1-a0=-1+32=31. 24.答案为:40;25.答案为:120;解析:因为二项式(1+2x)6的展开式中含x的项的系数为2C,二项式(1+y)5的展开式中含y3的项的系数为C,所以在多项式(1+2x)6(1+y)5的展开式中,xy3的系数为2CC=120. 26.答案为:-2;解析:5的展开式的通项Tr+1=C(ax2)5-r×r=
22.答案为:-48;解析:因为展开式中各项系数的和为2,所以令x=1,得(1-a)×1=2,解得a=-1.5展开式的通项公式为Tr+1=C(2x)5-rr=(-1)r25-rCx5-2r,令5-2r=3,得r=1,展开式中含x3项的系数为T2=(-1)×24C=-80,令5-2r=5,得r=0,展开式中含x5项的系数为T1=25C=32,所以5的展开式中含x4项的系数为-80+32=-48. 23.答案为:31;解析:令x=-1可得a0=-32.令x=0可得a0+a1+a2+a3+a4+a5=-1,所以a1+a2+a3+a4+a5=-1-a0=-1+32=31. 24.答案为:40;25.答案为:120;解析:因为二项式(1+2x)6的展开式中含x的项的系数为2C,二项式(1+y)5的展开式中含y3的项的系数为C,所以在多项式(1+2x)6(1+y)5的展开式中,xy3的系数为2CC=120. 26.答案为:-2;解析:5的展开式的通项Tr+1=C(ax2)5-r×r=![]() ,令10-=0,得r=4,所以Ca5-4=-10,解得a=-2. 27.答案为:0;解析:二项展开式的通项Tr+1=Cx9-rr=arCx9-2r,令9-2r=3,得r=3,所以a3C=-84,所以a=-1,所以二项式为9,令x=1,则(1-1)9=0,所以展开式的各项系数之和为0. 28.答案为:8;解析:n的展开式的通项Tr+1=Cxn-rr=C2-rxn-2r,则前三项的系数分别为1,,,由其依次成等差数列,得n=1+,解得n=8或n=1(舍去),故n=8. 29.答案为:3;解析:因为(1-2x)5的展开式中的常数项为1,x的系数为C×(-2)=-10;(1+ax)4的展开式中的常数项为1,x的系数为C·a=4a,所以(1-2x)5(1+ax)4的展开式中x的系数为1×4a+1×(-10)=2,所以a=3. 30.答案为:17.5;
,令10-=0,得r=4,所以Ca5-4=-10,解得a=-2. 27.答案为:0;解析:二项展开式的通项Tr+1=Cx9-rr=arCx9-2r,令9-2r=3,得r=3,所以a3C=-84,所以a=-1,所以二项式为9,令x=1,则(1-1)9=0,所以展开式的各项系数之和为0. 28.答案为:8;解析:n的展开式的通项Tr+1=Cxn-rr=C2-rxn-2r,则前三项的系数分别为1,,,由其依次成等差数列,得n=1+,解得n=8或n=1(舍去),故n=8. 29.答案为:3;解析:因为(1-2x)5的展开式中的常数项为1,x的系数为C×(-2)=-10;(1+ax)4的展开式中的常数项为1,x的系数为C·a=4a,所以(1-2x)5(1+ax)4的展开式中x的系数为1×4a+1×(-10)=2,所以a=3. 30.答案为:17.5;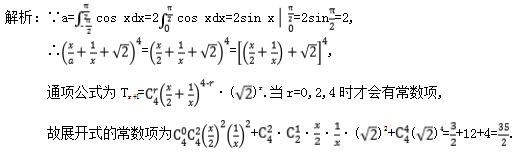
相关试卷
这是一份高考数学二轮复习题海集训34 导数的计算(30题含答案),共6页。
这是一份高考数学二轮复习题海集训32 双曲线(30题含答案),共10页。试卷主要包含了故选C,由左焦点F,等内容,欢迎下载使用。
这是一份高考数学二轮复习题海集训31 椭圆(30题含答案),共9页。









