

四川省成都市石室中学2022-2023学年高三上学期一诊数学(文科)模拟试题6
展开
这是一份四川省成都市石室中学2022-2023学年高三上学期一诊数学(文科)模拟试题6,共5页。试卷主要包含了 已知集合,,则,已知,则,已知实数满足则的最小值为等内容,欢迎下载使用。
![]() 成都石室中学高2023届数学一诊模拟试题六(文科)一. 选择题1. 已知复数z满足
成都石室中学高2023届数学一诊模拟试题六(文科)一. 选择题1. 已知复数z满足![]() ,则z在复平面内对应的点位于( )A.第一象限 B.第二象限 C.第三象限 D.第四象限2. 已知集合
,则z在复平面内对应的点位于( )A.第一象限 B.第二象限 C.第三象限 D.第四象限2. 已知集合![]() ,
,![]() ,则
,则![]() ( )A.
( )A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 3.已知
3.已知![]() ,则
,则![]() ( )A.
( )A.![]() B.
B.![]() C.
C.![]() D.
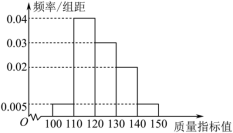
D.![]() 4.为了调查某工厂生产的一批口罩的质量情况,随机抽取了1000个口罩,所得数据如下图所示,据此估计,这批口罩质量指标值的众数(同一组中的数据用该组区间的中点值做代表)与中位数之和为与中位数之和为( )
4.为了调查某工厂生产的一批口罩的质量情况,随机抽取了1000个口罩,所得数据如下图所示,据此估计,这批口罩质量指标值的众数(同一组中的数据用该组区间的中点值做代表)与中位数之和为与中位数之和为( )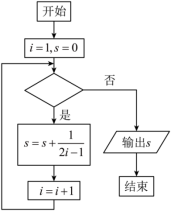 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.已知实数
5.已知实数![]() 满足
满足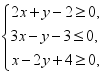 则
则![]() 的最小值为( )A.
的最小值为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.执行如图所示的程序框图,若输出的结果
6.执行如图所示的程序框图,若输出的结果![]() ,则判断框中填入的条件可以为( )A.
,则判断框中填入的条件可以为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.已知圆台上底面半径为1,下底面半径为3,球与圆台的两个底面和侧面均相切,则该圆台的侧面积与球的表面积之比为( )A.
7.已知圆台上底面半径为1,下底面半径为3,球与圆台的两个底面和侧面均相切,则该圆台的侧面积与球的表面积之比为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.双曲线
8.双曲线![]() 的焦点在圆
的焦点在圆![]() 上,圆
上,圆![]() 与双曲线
与双曲线![]() 的渐近线在第一、四象限分别交于
的渐近线在第一、四象限分别交于![]() 两点,
两点,![]() 满足
满足![]() (其中
(其中![]() 是坐标原点),则
是坐标原点),则![]() 的面积是( )A.6 B.
的面积是( )A.6 B.![]() C.12 D.189.已知函数
C.12 D.189.已知函数![]() 是定义域为R的偶函数
是定义域为R的偶函数![]() 为奇函数,当
为奇函数,当![]() 时,
时,![]() ,若
,若![]() ,则
,则![]() ( )A. 3 B. 2 C. -3 D. -610.已知数列
( )A. 3 B. 2 C. -3 D. -610.已知数列![]() 中,
中,![]() ,
,![]() ,当
,当![]() 时,
时,![]() 为定值,则实数
为定值,则实数![]() 的不同的值有( )A.4个 B.5个 C.6个 D.7个11.已知函数
的不同的值有( )A.4个 B.5个 C.6个 D.7个11.已知函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时,![]() ,则不等式
,则不等式![]() 的解集为(其中e为自然对数的底数)( )A.
的解集为(其中e为自然对数的底数)( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 12.已知抛物线
12.已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是
是![]() 的准线与
的准线与![]() 轴的交点,
轴的交点,![]() 是
是![]() 上一点,
上一点,![]() 的平分线与
的平分线与![]() 轴交于点
轴交于点![]() ,则
,则![]() 的最大值为( )A.
的最大值为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二.填空题13.已知平面向量
二.填空题13.已知平面向量![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() (其中
(其中![]() 表示向量
表示向量![]() ,
,![]() 的夹角),则
的夹角),则![]() .14.已知函数
.14.已知函数![]() ,将函数
,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,所得图象与原函数图象重合,则
个单位长度后,所得图象与原函数图象重合,则![]() 的最小值等于 .15.已知
的最小值等于 .15.已知![]() ,则当
,则当![]() 取得最小值时,
取得最小值时,![]() .
.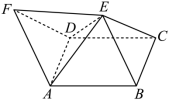 16.如图,正四棱锥
16.如图,正四棱锥![]() 的底面边长与侧棱长均为
的底面边长与侧棱长均为![]() ,正三棱锥
,正三棱锥![]() 的棱长均为
的棱长均为![]() ,下列四个命题中,正确命题的序号是 .(填写正确命题的序号)①
,下列四个命题中,正确命题的序号是 .(填写正确命题的序号)①![]() ; ②正四棱锥
; ②正四棱锥![]() 的内切球半径为
的内切球半径为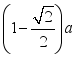 ;③
;③![]() ,
,![]() ,
,![]() ,
,![]() 四点共面; ④平面
四点共面; ④平面 ![]() 平面
平面![]() 三.解答题17.已知
三.解答题17.已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,且
,且![]() .(1)求角
.(1)求角![]() 的大小;(2)若
的大小;(2)若![]() 边上的高为
边上的高为![]() .求
.求![]() .
. 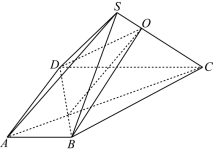 18. 如图,已知在四棱锥
18. 如图,已知在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,平面
,平面![]() ⊥平面
⊥平面![]() .(1)求证:平面
.(1)求证:平面![]() ⊥平面
⊥平面![]() ;(2)若直线
;(2)若直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,求
,求![]() 的值.
的值.  19. 为了调查某地区程序员的工资情况,研究人员随机抽取了该地区20名程序员作调查,所得数据
19. 为了调查某地区程序员的工资情况,研究人员随机抽取了该地区20名程序员作调查,所得数据![]() 的茎叶图如下所示(单位:元),其中
的茎叶图如下所示(单位:元),其中![]() ,经计算得
,经计算得![]() ,
,![]() .(1)求被调查的这20名程序员的平均工资
.(1)求被调查的这20名程序员的平均工资![]() ;(2)在(1)的条件下,可以算得
;(2)在(1)的条件下,可以算得![]() ,求“
,求“![]() ,
,![]() ,
,![]() ,
,![]() ”的方差
”的方差![]() ;(3)若从被调查的这20名程序员中随机抽取工资不足6501元的2名程序员,求至少有1名程序员的工资在6000元以下的概率. 20. 已知椭圆C:
;(3)若从被调查的这20名程序员中随机抽取工资不足6501元的2名程序员,求至少有1名程序员的工资在6000元以下的概率. 20. 已知椭圆C:![]() 的左、右顶点分别为A,B,点M是椭圆C的上顶点,且
的左、右顶点分别为A,B,点M是椭圆C的上顶点,且![]() ,
,![]() .(1)求椭圆C的方程;(2)已知
.(1)求椭圆C的方程;(2)已知![]() ,其中O为坐标原点,过点D的直线
,其中O为坐标原点,过点D的直线![]() 与椭圆C交于E,G两点,点H在椭圆C上,探究:是否存在直线
与椭圆C交于E,G两点,点H在椭圆C上,探究:是否存在直线![]() ,使得四边形OEHG为矩形,若存在,求出直线
,使得四边形OEHG为矩形,若存在,求出直线![]() 的方程;若不存在,请说明理由. 21.已知函数
的方程;若不存在,请说明理由. 21.已知函数![]() .(1)判断函数
.(1)判断函数![]() 在区间
在区间![]() 上零点的个数;(2)设函数
上零点的个数;(2)设函数![]() 在区间
在区间![]() 上的极值点从小到大分别为
上的极值点从小到大分别为![]() .证明:(i)
.证明:(i)![]() ;(ii)对一切
;(ii)对一切![]() ,
,![]() 成立. 22.在平面直角坐标系
成立. 22.在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),已知点
为参数),已知点![]() ,点
,点![]() 是曲线
是曲线![]() 上任意一点,点
上任意一点,点![]() 满足
满足![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.(1)求点
轴正半轴为极轴建立极坐标系.(1)求点![]() 的轨迹
的轨迹![]() 的极坐标方程;(2)已知直线
的极坐标方程;(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
相关试卷
这是一份四川省成都市石室中学2024届高三上学期一诊模拟考试文科数学,文件包含石室中学高2024届2023-2024学年度上期一诊模拟数学文科A卷40文科答案docx、石室中学高2024届2023-2024学年度上期一诊模拟数学文科A卷40docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
这是一份四川省成都市石室中学2023-2024学年高三上学期一诊模拟考试数学(文科)试卷,文件包含石室中学高2024届2023-2024学年度上期一诊模拟数学文科A卷40文科答案docx、石室中学高2024届2023-2024学年度上期一诊模拟数学文科A卷40docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
这是一份四川省成都市石室中学2022-2023学年高三上学期一诊数学(文科)模拟试题十,共16页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。









