专题02 一元二次函数 、 方程和不等式（公式、定理、结论图表）-备战2024年新高考数学必背知识手册

这是一份专题02 一元二次函数 、 方程和不等式（公式、定理、结论图表）-备战2024年新高考数学必背知识手册，共12页。试卷主要包含了不等关系，实数a，b的比较大小，等式的性质，不等式的基本性质，基本不等式，一元二次不等式的概念，一元二次不等式的一般形式，一元二次不等式的解与解集等内容，欢迎下载使用。
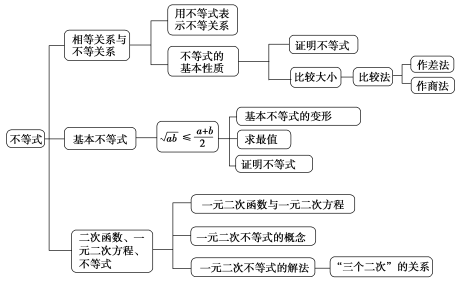
  一元二次函数、方程和不等式（公式、定理、结论图表）1．不等关系不等关系常用不等式来表示．2．实数a，b的比较大小文字语言数学语言等价条件a－b是正数a－b＞0a＞ba－b等于零a－b＝0a＝ba－b是负数a－b＜0a＜b3.重要不等式一般地，∀a，b∈R，有a2＋b2≥2ab，当且仅当a＝b时，等号成立．4．等式的性质(1) 性质1 如果a＝b，那么b＝a；(2) 性质2 如果a＝b，b＝c，那么a＝c；(3) 性质3 如果a＝b，那么a±c＝b±c；(4) 性质4 如果a＝b，那么ac＝bc；(5) 性质5 如果a＝b，c≠0，那么＝.5．不等式的基本性质(1)对称性：a＞b⇔b＜a.(2)传递性：a＞b，b＞c⇒a＞c.(3)可加性：a＞b⇔a＋c＞b＋c.(4)可乘性：a＞b，c＞0⇒ac＞bc；a＞b，c＜0⇒ac＜bc.(5)加法法则：a＞b，c＞d⇒a＋c＞b＋d.(6)乘法法则：a＞b＞0，c＞d＞0⇒ac＞bd.(7)乘方法则：a＞b＞0⇒an＞bn＞0(n∈N，n≥2)．6．基本不等式(1)有关概念：当a，b均为正数时，把叫做正数a，b的算术平均数，把叫做正数a，b的几何平均数．(2)不等式：当a，b是任意正实数时，a，b的几何平均数不大于它们的算术平均数，即≤，当且仅当a＝b时，等号成立．7.已知x、y都是正数，(1)若x＋y＝S(和为定值)，则当x＝y时，积xy取得最大值.(2)若xy＝p(积为定值)，则当x＝y时，和x＋y取得最小值2.上述命题可归纳为口诀：积定和最小，和定积最大．8．一元二次不等式的概念只含有一个未知数，并且未知数的最高次数是2的不等式，称为一元二次不等式．9．一元二次不等式的一般形式(1)ax2＋bx＋c＞0(a≠0)．(2)ax2＋bx＋c≥0(a≠0)．(3)ax2＋bx＋c＜0(a≠0)．(4)ax2＋bx＋c≤0(a≠0)．思考1：不等式x2－y2>0是一元二次不等式吗？提示：此不等式含有两个变量，根据一元二次不等式的定义，可知不是一元二次不等式．10．一元二次不等式的解与解集使一元二次不等式成立的未知数的值，叫做这个一元二次不等式的解，其解的集合，称为这个一元二次不等式的解集．思考2：类比“方程x2＝1的解集是{1，－1}，解集中的每一个元素均可使等式成立”．不等式x2>1的解集及其含义是什么？提示：不等式x2>1的解集为{x|x<－1或x>1}，该集合中每一个元素都是不等式的解，即不等式的每一个解均使不等式成立．11．三个“二次”的关系设y＝ax2＋bx＋c(a＞0)，方程ax2＋bx＋c＝0的判别式Δ＝b2－4ac判别式Δ＞0Δ＝0Δ＜0解不等式y＞0或y＜0的步骤求方程y＝0的解有两个不相等的实数根x1，x2(x1＜x2)有两个相等的实数根x1＝x2＝－没有实数根画函数y＝ax2＋bx＋c(a＞0)的图象得等的集不式解y＞0{x|x＜x1_或x＞x2}Ry＜0{x|x1＜x＜x2}∅∅思考3：若一元二次不等式ax2＋x－1>0的解集为R，则实数a应满足什么条件？提示：结合二次函数图象可知，若一元二次不等式ax2＋x－1>0的解集为R，则解得a∈∅，所以不存在a使不等式ax2＋x－1>0的解集为R.12．分式不等式的解法主导思想：化分式不等式为整式不等式类型同解不等式＞0(＜0)(其中a，b，c，d为常数)法一：或法二：(ax＋b)(cx＋d)＞0(＜0)≥0(≤0)法一：或法二：＞k(其中k为非零实数)先移项通分转化为上述两种形式思考1：>0与(x－3)(x＋2)>0等价吗？将>0变形为(x－3)(x＋2)>0，有什么好处？提示：等价；好处是将不熟悉的分式不等式化归为已经熟悉的一元二次不等式．13．(1)不等式的解集为R(或恒成立)的条件不等式ax2＋bx＋c>0ax2＋bx＋c<0a＝0b＝0，c>0b＝0，c<0a≠0(2)有关不等式恒成立求参数的取值范围的方法设二次函数y＝ax2＋bx＋c若ax2＋bx＋c≤k恒成立⇔ymax≤k若ax2＋bx＋c≥k恒成立⇔ymin≥k14.从实际问题中抽象出一元二次不等式模型的步骤(1)阅读理解，认真审题，分析题目中有哪些已知量和未知量，找准不等关系．(2)设出起关键作用的未知量，用不等式表示不等关系(或表示成函数关系)．(3)解不等式(或求函数最值)．(4)回扣实际问题．思考2：解一元二次不等式应用题的关键是什么？提示：解一元二次不等式应用题的关键在于构造一元二次不等式模型，选择其中起关键作用的未知量为x，用x来表示其他未知量，根据题意，列出不等关系再求解．<解题方法与技巧>1．作差法比较大小的一般步骤第一步：作差；第二步：变形，常采用配方、因式分解等恒等变形手段，将“差”化成“和”或“积”；第三步：定号，就是确定是大于0，等于0，还是小于0(不确定的要分情况讨论)；最后得结论．概括为“三步一结论”，这里的“定号”是目的，“变形”是关键.典例1：已知x≤1，比较3x3与3x2－x＋1的大小．[解] 3x3－(3x2－x＋1)＝(3x3－3x2)＋(x－1)＝3x2(x－1)＋(x－1)＝(3x2＋1)(x－1)．∵x≤1得x－1≤0，而3x2＋1＞0，∴(3x2＋1)(x－1)≤0，∴3x3≤3x2－x＋1.2.利用不等式的性质证明不等式注意事项1利用不等式的性质及其推论可以证明一些不等式.解决此类问题一定要在理解的基础上，记准、记熟不等式的性质并注意在解题中灵活准确地加以应用.2应用不等式的性质进行推导时，应注意紧扣不等式的性质成立的条件，且不可省略条件或跳步推导，更不能随意构造性质与法则.典例2：若a＞b＞0，c＜d＜0，e＜0，求证：＞.[思路点拨]　可结合不等式的基本性质，分析所证不等式的结构，有理有据地导出证明结果．[证明]　∵c＜d＜0，∴－c＞－d＞0.又∵a＞b＞0，∴a－c＞b－d＞0.∴(a－c)2＞(b－d)2＞0.两边同乘以，得＜.又e＜0，∴＞.3. 对基本不等式的理解1．基本不等式≤ (a＞0，b＞0)反映了两个正数的和与积之间的关系．2．对基本不等式的准确掌握要抓住以下两个方面：(1)定理成立的条件是a、b都是正数．(2)“当且仅当”的含义：当a＝b时，≤的等号成立，即a＝b⇒＝；仅当a＝b时，≥的等号成立，即＝⇒a＝b.典例3：给出下面四个推导过程：①∵a、b为正实数，∴＋≥2＝2；②∵a∈R，a≠0，∴＋a≥2＝4；③∵x、y∈R，xy＜0，∴＋＝－≤－2＝－2.其中正确的推导为(　　)A．①②　　　　 B．①③C．②③   D．①②③B [解]①∵a、b为正实数，∴、为正实数，符合基本不等式的条件，故①的推导正确．②∵a∈R，a≠0，不符合基本不等式的条件，∴＋a≥2＝4是错误的．③由xy＜0，得、均为负数，但在推导过程中将整体＋提出负号后，、均变为正数，符合均值不等式的条件，故③正确．]4.利用基本不等式比较大小1．在理解基本不等式时，要从形式到内含中理解，特别要关注条件．2．运用基本不等式比较大小时应注意成立的条件，即a＋b≥2成立的条件是a>0，b>0，等号成立的条件是a＝b；a2＋b2≥2ab成立的条件是a，b∈R，等号成立的条件是a＝b.典例4：(1)已知a，b∈R＋，则下列各式中不一定成立的是(　　)A．a＋b≥2   B.＋≥2C.≥2   D.≥(2)已知a，b，c是两两不等的实数，则p＝a2＋b2＋c2与q＝ab＋bc＋ca的大小关系是________．(1)D (2)a2＋b2＋c2＞ab＋bc＋ac[解](1)由≥得a＋b＝2，∴A成立；∵＋≥2＝2，∴B成立；∵≥＝2，∴C成立；∵≤＝，∴D不一定成立．(2)∵a、b、c互不相等，∴a2＋b2＞2ab，b2＋c2>2ac，a2＋c2>2ac.∴2(a2＋b2＋c2)>2(ab＋bc＋ac)．即a2＋b2＋c2>ab＋bc＋ac.]5.利用基本不等式证明不等式1．条件不等式的证明，要将待证不等式与已知条件结合起来考虑，比如本题通过“1”的代换，将不等式的左边化成齐次式，一方面为使用基本不等式创造条件，另一方面可实现约分与不等式的右边建立联系．2．先局部运用基本不等式，再利用不等式的性质(注意限制条件)，通过相加(乘)合成为待证的不等式，既是运用基本不等式时的一种重要技能，也是证明不等式时的一种常用方法．典例5：已知a，b，c是互不相等的正数，且a＋b＋c＝1，求证：＋＋>9.[思路点拨]　看到＋＋>9，想到将“1”换成“a＋b＋c”，裂项构造基本不等式的形式，用基本不等式证明．[证明]∵a，b，c∈R＋，且a＋b＋c＝1，∴＋＋＝＋＋＝3＋＋＋＋＋＋＝3＋＋＋≥3＋2＋2＋2＝3＋2＋2＋2＝9.当且仅当a＝b＝c时取等号，∴＋＋>9.6.利用基本不等式求最值利用基本不等式求最值的关键是获得满足基本不等式成立条件，即“一正、二定、三相等”.解题时应对照已知和欲求的式子运用适当的“拆项、添项、配凑、变形”等方法创设应用基本不等式的条件.具体可归纳为三句话：若不正，用其相反数，改变不等号方向；若不定应凑出定和或定积；典例6：(1)已知x<，求y＝4x－2＋的最大值；(2)已知0<x<，求y＝x(1－2x)的最大值．[思路点拨]　(1)看到求y＝4x－2＋的最值，想到如何才能出现乘积定值；(2)要求y＝x(1－2x)的最值，需要出现和为定值．[解](1)∵x<，∴5－4x>0，∴y＝4x－2＋＝－＋3≤－2＋3＝1，当且仅当5－4x＝，即x＝1时，上式等号成立，故当x＝1时，ymax＝1.(2)∵0<x<，∴1－2x>0，∴y＝×2x(1－2x)≤×2＝×＝.∴当且仅当2x＝1－2x，即x＝时，ymax＝.7.利用基本不等式求条件最值1．本题给出的方法，用到了基本不等式，并且对式子进行了变形，配凑出满足基本不等式的条件，这是经常使用的方法，要学会观察、学会变形．2．常见的变形技巧有：(1)配凑系数；(2)变符号；(3)拆补项．常见形式有f(x)＝ax＋型和f(x)＝ax(b－ax)型．典例7：已知x＞0，y＞0，且满足＋＝1.求x＋2y的最小值．[解]∵x＞0，y＞0，＋＝1，∴x＋2y＝(x＋2y)＝10＋＋≥10＋2＝18，当且仅当即时，等号成立，故当x＝12，y＝3时，(x＋2y)min＝18.8.利用基本不等式解决实际问题1．在应用基本不等式解决实际问题时，应注意如下思路和方法：(1)先理解题意，设出变量，一般把要求最值的量定为函数；(2)建立相应的函数关系，把实际问题抽象成函数的最大值或最小值问题；(3)在定义域内，求出函数的最大值或最小值；(4)正确写出答案．2．对于函数y＝x＋(k>0)，可以证明0＜x≤及－≤x＜0上均为减函数，在x≥及x≤－上都是增函数．求此函数的最值时，若所给的范围含±时，可用基本不等式，不包含±时，可用函数的单调性求解典例8：如图，动物园要围成相同面积的长方形虎笼四间，一面可利用原有的墙，其他各面用钢筋网围成．现有36 m长的钢筋网材料，每间虎笼的长、宽分别设计为多少时，可使每间虎笼面积最大？[解]设每间虎笼长x m，宽y m，则由条件知，4x＋6y＝36，即2x＋3y＝18.设每间虎笼面积为S，则S＝xy.法一：由于2x＋3y≥2＝2，所以2≤18，得xy≤，即Smax＝，当且仅当2x＝3y时，等号成立．由解得故每间虎笼长为4.5 m，宽为3 m时，可使每间虎笼面积最大．法二：由2x＋3y＝18，得x＝9－y.∵x>0，∴0<y<6，S＝xy＝y＝y(6－y)．∵0<y<6，∴6－y>0.∴S≤2＝.当且仅当6－y＝y，即y＝3时，等号成立，此时x＝4.5.故每间虎笼长为4.5 m，宽为3 m时，可使每间虎笼面积最大．9.不等式恒成立问题 对于恒成立不等式求参数范围问题常见类型及解法有以下两种：1变更主元法根据实际情况的需要确定合适的主元，一般知道取值范围的变量要看作主元.2转化法求参数范围已知二次函数y＝ax2＋bx＋c的函数值的集合为B＝{y|m≤y≤n}，则1y≥k恒成立⇒ymin≥k即m≥k；2y≤k恒成立⇒ymax≤k即n≤k.典例9：已知y＝x2＋ax＋3－a，若－2≤x≤2，x2＋ax＋3－a≥0恒成立，求a的取值范围．[思路点拨]　对于含参数的函数在某一范围上的函数值恒大于等于零的问题，可以利用函数的图象与性质求解．[解]设函数y＝x2＋ax＋3－a在－2≤x≤2时的最小值为关于a的一次函数，设为g(a)，则(1)当对称轴x＝－<－2，即a>4时，g(a)＝(－2)2＋(－2)a＋3－a＝7－3a≥0，解得a≤，与a>4矛盾，不符合题意．(2)当－2≤－≤2，即－4≤a≤4时，g(a)＝3－a－≥0，解得－6≤a≤2，此时－4≤a≤2.(3)当－>2，即a<－4时，g(a)＝22＋2a＋3－a＝7＋a≥0，解得a≥－7，此时－7≤a<－4.综上，a的取值范围为－7≤a≤2.