数学人教版9年级上册第23单元精准教学★★★题库

这是一份数学人教版9年级上册第23单元精准教学★★★题库，共32页。









数学人教版


数学人教版9年级上册
第23单元精准教学★★★题库
一、单选题
1．下列图形中，既是中心对称图形又是轴对称图形的是（　　）
A．正六边形 B．正五边形 C．平行四边形 D．正三角形
2．如图，三角形绕点逆时针旋转，得到三角形，若，则等于（    ）

A． B． C． D．
3．如图，将绕点C顺时针旋转，点B的对应点为点E，点A的对应点为点D，当点E恰好落在边上时，连接，若，则的度数是（    ）

A． B． C． D．
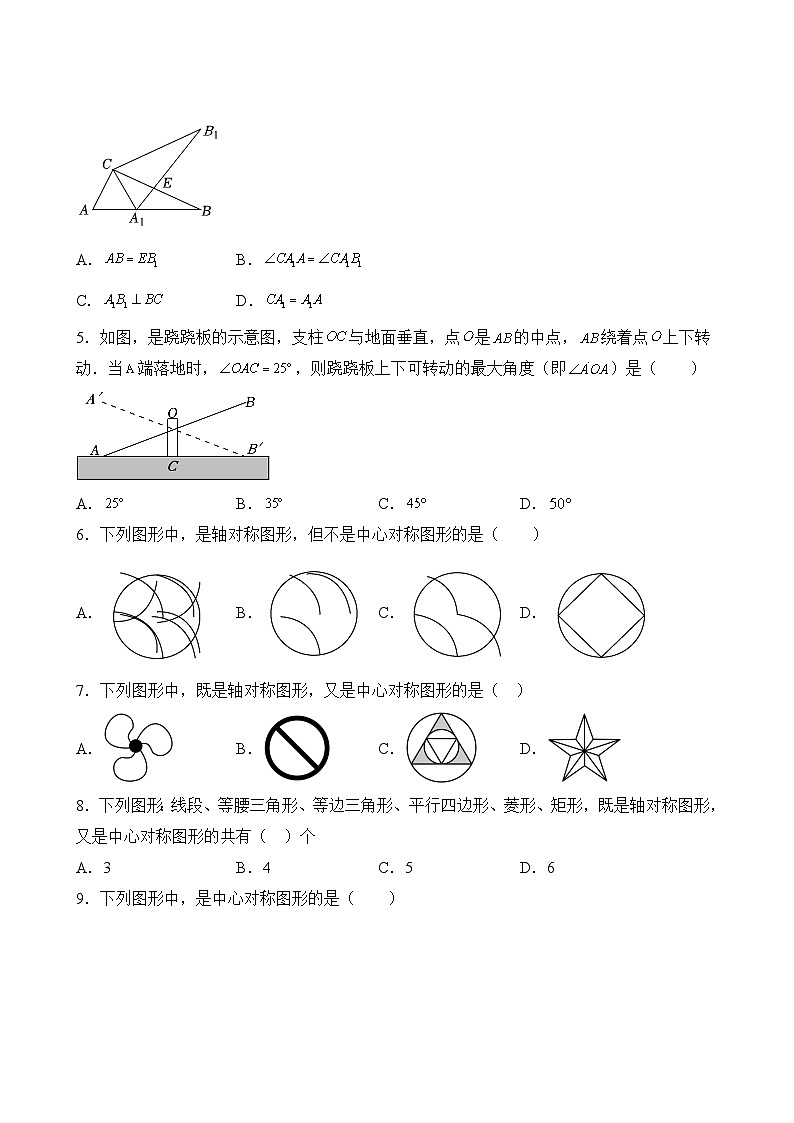
4．如图，在中，，将绕点逆时针旋转得到，此时使点的对应点恰好在边上，点的对应点为，与交于点，则下列结论一定正确的是（    ）

A． B．
C． D．
5．如图，是跷跷板的示意图，支柱与地面垂直，点是的中点，绕着点上下转动．当端落地时，，则跷跷板上下可转动的最大角度（即）是（　　）

A． B． C． D．
6．下列图形中，是轴对称图形，但不是中心对称图形的是（　　）
A． B． C． D．
7．下列图形中，既是轴对称图形，又是中心对称图形的是（    ）
A． B． C． D．
8．下列图形：线段、等腰三角形、等边三角形、平行四边形、菱形、矩形，既是轴对称图形，又是中心对称图形的共有（    ）个
A．3 B．4 C．5 D．6
9．下列图形中，是中心对称图形的是（　　）
A． B．
C． D．
10．2022年2月第24届冬季奥林匹克运动会在我国北京成功举办，以下是参选的冬奥会会徽设计的部分图形，其中既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
11．剪纸是我国具有独特艺术风格的民间艺术，反映了劳动人民对现实生活的深刻感悟.下列剪纸图形中，是中心对称图形的有（　　　）

①     　　　　　②　　　　　　　　　　 ③　　　　　　　　　　④
A．①②③ B．①②④ C．①③④ D．②③④
12．将四个数字看作一个图形，则下列四个图形中，是中心对称图形的是（    ）
A． B． C． D．
13．下列垃圾分类的标志中，既是轴对称图形又是中心对称图形的是（　　）
A．可回收物 B．厨余垃圾
C．有害垃圾 D．其它垃圾物
14．下列图形中既是轴对称又是中心对称图形的是（    ）
A． B． C． D．
15．在如图所示的方格纸（1格长为1个单位长度）中，△ABC的顶点都在格点上，将△ABC绕点O按顺时针方向旋转得到△A'B'C'使各顶点仍在格点上，则其旋转角的度数是（    ）

A．30° B．60° C．75° D．90°
16．如图，将绕点按逆时针方向旋转后得到，若，则的度数是（    ）

A． B． C． D．
17．如图，将木条a，b与c钉在一起，∠1＝85°，∠2＝45°，要使木条a与b平行，木条a按箭头方向旋转的度数至少是（　　）

A．15° B．25° C．35° D．40°
18．在平面直角坐标系中，点关于原点对称的点的坐标是（   ）
A． B． C． D．
19．如图，该图案绕它的中心至少旋转m度能与自身完全重合，则m的值是（    ）

A．45 B．90 C．135 D．180
20．如图，在平面直角坐标系中，点A，C在x轴上，点C的坐标为，．将先绕点C顺时针旋转，再向右平移4个单位长度，则变换后点A的对应点坐标是(   )

A． B． C． D．
21．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
22．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
23．下列图形是中心对称图形，也是轴对称图形的是（    ）
A． B． C． D．
24．下面图形中既是轴对称图形又是中心对称图形的是（   ）
科克曲线笛卡尔心形线
阿基米德螺旋线赵爽弦图
A．科克曲线 B．笛卡尔心形线 C．阿基米德螺旋线 D．赵爽弦图
25．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A． B．
C． D．
26．如图，在中，，在同一平面内，将绕点旋转到△的位置，使得，则等于（　　）

A． B． C． D．
27．围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史．以下是在棋谱中截取的四个部分，由黑白棋子摆成的图案是中心对称图形的是（    ）
A． B． C． D．
28．如图，中，，，点D是边上一动点，以点A为旋转中心，将顺时针旋转得到线段，连接，若，则的长的最小值为（    ）

A． B． C．1 D．
29．如图，将矩形绕点A顺时针旋转到矩形的位置，若旋转角为，则为（    ）

A． B． C． D．
30．如图，在△ABC中，把△ABC绕着点A顺时针旋转42°，得到△，点C的对应点落在BC边上，则∠B的度数为（　　）

A．84° B．69° C．111° D．138°
二、填空题
31．已知点和点关于原点对称，则______．
32．在平面直角坐标系中，已知点与点关于原点对称，则___________．
33．已知点A（﹣2，b）与点B（a，3）关于原点对称，则a﹣b =______．
34．已知点A（2，4）与点B（b–1，2a）关于原点对称，则a=___，b=_____．
35．若点与关于原点对称，则____．
36．如图，在中，，将绕点A按逆时针方向旋转得到．若点恰好落在边上，且，则的度数为 ________．

37．如图，正方形的边长为4，点是边上一点，，将线段绕点旋转，使点落在直线上，落点记为，则的长为______．

38．如图，绕点C逆时针旋转后得，如果点B、D、E在一直线上，且，那么A、D两点间的距离是_________．

39．如图，在平面直角坐标系中，点A、C在x轴上，点C的坐标为（﹣1，0），AC=2．将Rt△ABC先绕点C顺时针旋转90°，再向右平移3个单位长度，则变换后点A的对应点坐标是_______．

40．如图，图中网格由边长为1的小正方形组成，点为网格线的交点.若线段绕原点顺时针旋转90°后，端点的坐标变为______．

三、解答题
41．如图，将绕点顺时针旋转后得，若，求的度数．  

42．如图，在中，，点O是上的中点，将绕着点O旋转得

(1)求证：四边形是菱形；
(2)如果，求菱形的面积．
43．如图，在中，，将绕点A顺时针方向旋转到的位置，连接，求的度数．

44．如图，的顶点坐标为，，．

(1)画出关于x轴对称的；
(2)将绕原点O旋转，画出旋转后的；
(3)与关于______对称．
45．如图，将绕直角顶点顺时针旋转，得到，连接，

(1)求的长
(2)若，求的度数．
46．如图，在中，，将绕点B逆时针旋转到的延长线与相交于点F，连接，求证：．

47．如图，在平面直角坐标系中，各顶点的坐标为，各顶点的坐标为．

(1)在图中作出关于y轴对称的；
(2)若与关于点P成中心对称，则点P的坐标是___．
48．图①、图②均为7×6的正方形网格，点A，B，C在格点（小正方形的顶点）上．

(1)在图①中确定格点，并画出一个以A、B、C、D为顶点的四边形，使其为中心对称图形，但不是轴对称图形．
(2)在图②中确定格点，并画出以A、B、C、E为顶点的四边形，使其为轴对称图形，但不是中心对称图形．
49．已知的三个顶点的坐标分别为、、．

(1)画出关于坐标原点成中心对称的；
(2)将绕坐标原点顺时针旋转，画出对应的；
(3)若以、、、为顶点的四边形为平行四边形，请直接写出的坐标　　．
50．如图，点在射线上，．如果绕点按逆时针方向旋转到，那么点的位置可以用表示．

(1)按上述表示方法，若，，则点的位置可以表示为______；
(2)在（1）的条件下，已知点的位置用表示，连接、．求证：．
51．图1，图2都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点，线段的端点均在格点上，分别按要求画出图形．

(1)在图1中画出等腰三角形，且点C在格点上．（画出一个即可）
(2)在图2中画出以为边的菱形，且点D，E均在格点上．
52．如图，在的方格纸中，已知格点P，请按要求画格点图形（顶点均在格点上）．

(1)在图1中画一个锐角三角形，使P为其中一边的中点，再画出该三角形向右平移2个单位后的图形．
(2)在图2中画一个以P为一个顶点的钝角三角形，使三边长都不相等，再画出该三角形绕点P旋转后的图形．
53．如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点）．

(1)将△ABC向上平移6个单位，再向右平移2个单位，得到，请画出﹔
(2)以边AC的中点O为旋转中心，将△ABC按逆时针方向旋转180°，得到，请画出．
54．如图，在由边长为1个单位长度的小正方形组成的网格中，给出了格点（顶点为网格线的交点）．

(1)将线段AB绕着点A逆时针旋转90°得到线段AP，请在图中画出线段AP；
(2)将作适当平移，使得点C与点P重合，请在图中画出平移后的．
55．阅读理解，并解答问题：
观察发现：
如图1是一块正方形瓷砖，分析发现这块瓷砖上的图案是按图2所示的过程设计的，其中虚线所在的直线是正方形的对称轴．

问题解决：
用四块如图1所示的正方形瓷砖按下列要求拼成一个新的大正方形，并在图3和图4中各画一种拼法．
(1)图3中所画拼图拼成的图案是轴对称图形，但不是中心对称图形；
(2)图4中所画拼图拼成的图案既是轴对称图形，又是中心对称图形．

56．已知△ABC中，∠ACB＝135°，将△ABC绕点A顺时针旋转90°，得到△AED，连接CD，CE．

(1)求证：△ACD为等腰直角三角形；
(2)若BC＝1，AC＝2，求四边形ACED的面积．
57．如图，在平面直角坐标系中，点A的坐标为，点B的坐标为，点C的坐标为．

(1)画出将向下平移5个单位长度得到的；
(2)画出将绕点原点O逆时针旋转90°后得到的，写出的坐标．
58．如图，点O是等边三角形ABC内的一点，∠BOC＝150°，将△BOC绕点C按顺时针方向旋转一定的角度，得到△ADC，连接OD，OA．

(1)求∠ODC的度数；
(2)试判断AD与OD的位置关系，并说明理由；
(3)若OB＝2，OC＝3，求AO的长（直接写出结果）．
59．如图，在平面直角坐标系中，已知点A（2，0），B（1，3）．

（1）画出线段AB，再画出线段AB关于原点对称的图形；
（2）画出线段AB绕点O逆时针旋转90°后的图形．
60．如图，在平面直角坐标中，的顶点坐标分别是，，．

（1）将以为旋转中心旋转，画出旋转后对应的；
（2）将平移后得到，若点的对应点的坐标为，求的面积

参考答案
1．A
2．B
3．D
4．B
5．D
6．C
7．B
8．A
9．C
10．C
11．A
12．D
13．C
14．A
15．D
16．B
17．D
18．C
19．A
20．A
21．B
22．D
23．A
24．A
25．A
26．D
27．B
28．A
29．B
30．C
31．3
32．
33．5
34． -2 -1
35．
36．/24度
37．9或1/1或9
38．
39．（2，2）
40．
41．解：∵将绕点顺时针旋转后得，  
∴，
∵，
∴，
∴．
42．（1）证明：∵将绕着点O旋转得，
∴，
∵，
∴，
∴四边形是菱形；
（2）解：如图，过点A作于点E，

∵，
∴是等边三角形，
∴，，
∴，
∴菱形的面积为．
43．解：∵绕点A顺时针方向旋转得到，
∴，，
∴为等边三角形，
∴，
∵，
∴．
44．（1）解：如图，即为所求；
（2）解：如图，即为所求；

（3），，
解：由（1）得：点，
由（2）得：，
∴与的三个顶点关于y轴对称，
∴与关于y轴对称．
故答案为：y轴
45．（1）∵将绕直角顶点顺时针旋转，得到，
∴，
∴
∴；
（2）∵，
∴是等腰直角三角形
∴
∴
∵
∴
∴．
46．解：由旋转得，
∴是等边三角形，
∴，
∵，
∴，
∴．
47．（1）解：如图所示，即为所求；

（2）解：如图所示，连接与交于点P，
由图可知点P的坐标为（此坐标可以利用P是的中点进行求解），
故答案啊为：．

48．（1）如图①所示：

四边形即为所求；
（2）如图②所示：

四边形即为所求．
49．（1）解：如图所示，△即为所求；
（2）解：如图所示，即为所求；
（3）解：的坐标、、．
故答案为：、、．

50．（1）解：由题意，得A′(a,n°)，
∵a=3,n=37，
∴A′(3,37°)，
故答案为：(3,37°)；
（2）证明：如图，

∵，B(3,74°)，
∴∠AOA′=37°，∠AOB=74°，OA= OB=3，
∴∠A′OB=∠AOB-∠AOA′=74°-37°=37°，
∵OA′=OA′，
∴△AOA′≌△BOA′（SAS），
∴A′A=A′B．
51．（1）答案不唯一．

（2）
52．（1）画法不唯一，如图1或图2等．

（2）画法不唯一，如图3或图4等．

53．（1）如图，即为所作；

（2）如图，即为所作；

54．（1）解：如图，线段AP即为所求；

（2）解：如图，即为所求.

55．（1）解：（1）参考图案，如图所示：

（2）（2）参考图案，如图所示：

56．（1）证明：∵△AED是△ABC旋转90°得到的，
，∠CAD＝90°，
∴AC＝AD，
∴△ACD是等腰直角三角形；
（2）解：∵△ACD是等腰直角三角形，
∴∠ADC＝∠ACD＝45°，AC＝AD＝2，
，
由(1)知，∠ADE＝∠ACB＝135°，
∴∠CDE＝∠ADE－∠ADC＝90°，
∵DE＝BC＝1，
∴．
57．（1）解：经过平移可得：，，，顺次连接，如图所示：即为所求作；

（2）解：旋转后的点的坐标分别为：，，，然后顺次连接，
如图所示：即为所求作，的坐标
58．（1）由旋转的性质得：，．
∴，即．
∵为等边三角形，∴．
∴．∴为等边三角形，．
（2）．
由旋转的性质得，．
∵，∴．
即．
（3）由旋转的性质得，AD=OB=2，
∵△OCD为等边三角形，
∴OD=OC=3，
在Rt△AOD中，由勾股定理得：
AO=
=
=
59．解：（1）线段AB关于原点对称的图形为线段CD，如图所示，
（2）分别作出点A、B绕点O旋转90°的对应点，分别为E、F，则线段EF即为所求，如图所示，

60．解：（1）延长至,使得；延长至,使得；延长至,使得；再连接即得旋转后对应的，如下图所示：

（2）由题意，，，平移后得到，其中，根据平移的规律知，平移过程是向下和向右分别移动两个单位可得：，
再连接点，得，其中交轴于点,如上图所示：

由得出直线的方程如下：
直线：
当时，，
，
,



故．