




还剩8页未读,
继续阅读
成套系列资料,整套一键下载
2023九年级数学上册第二十三章旋转专项2旋转中常见的几何模型作业课件新版新人教版
展开
这是一份2023九年级数学上册第二十三章旋转专项2旋转中常见的几何模型作业课件新版新人教版,共16页。
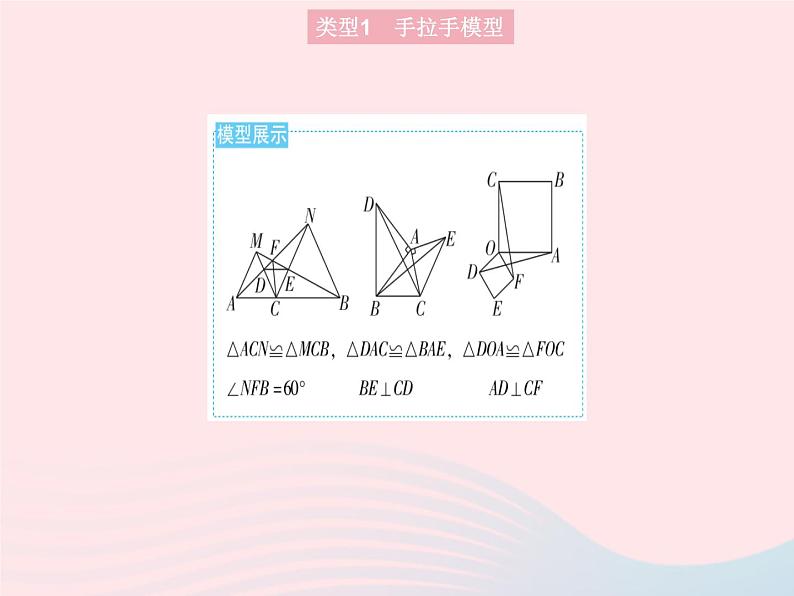
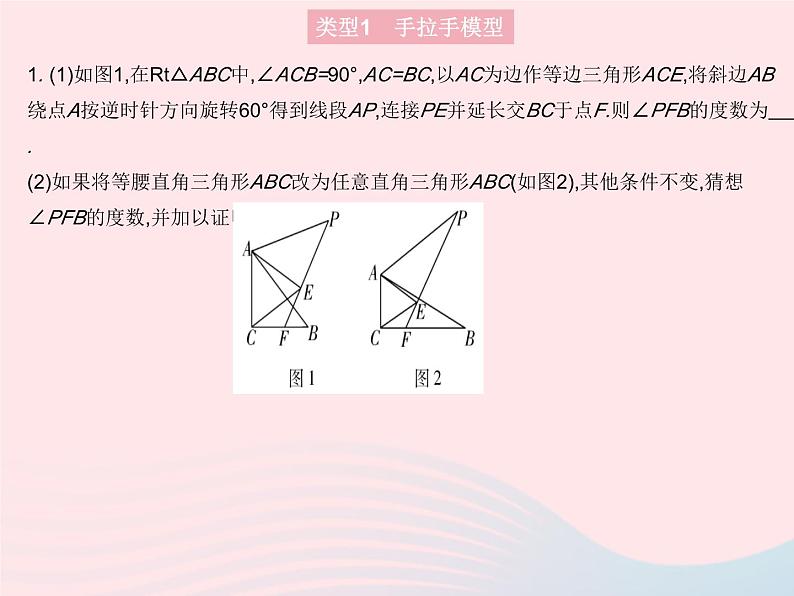
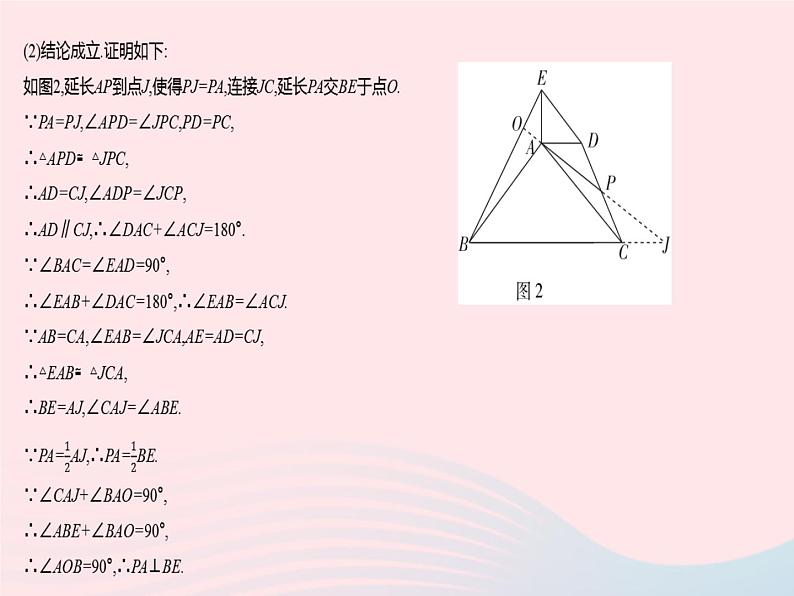
专项2 旋转中常见的几何模型类型1 手拉手模型1. (1)如图1,在Rt△ABC中,∠ACB=90°,AC=BC,以AC为边作等边三角形ACE,将斜边AB绕点A按逆时针方向旋转60°得到线段AP,连接PE并延长交BC于点F.则∠PFB的度数为 . (2)如果将等腰直角三角形ABC改为任意直角三角形ABC(如图2),其他条件不变,猜想∠PFB的度数,并加以证明.类型1 手拉手模型1.解:(1)60°(2)∠PFB=60°.证明如下:∵△ACE是等边三角形,∴∠CAE=∠ACE=∠AEC=60°,AE=AC.∵∠PAE=∠BAP+∠BAE=60°+∠BAE,∠BAC=∠CAE+∠BAE=60°+∠BAE,∴∠PAE=∠BAC. 由旋转可得AP=AB,∴△PAE≌△BAC,∴∠PEA=∠ACB=90°, ∴∠CEF=180°-∠PEA-∠AEC=180°-90°-60°=30°,又∠ECF=∠ACB-∠ACE=30°,∴∠PFB=∠ECF+∠CEF=30°+30°=60°.答案2. 【问题背景】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,BE,点P为DC的中点.(1)【观察猜想】观察图1,猜想线段AP与BE的数量关系是 ,位置关系是 . (2)【拓展探究】把△ADE绕点A逆时针旋转到图2的位置,(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,写出新的结论并说明理由.(3)【问题解决】把△ADE绕点A在平面内自由旋转,若DE=4,BC=8,请直接写出线段AP的取值范围.类型1 手拉手模型 答案 类型2 半角模型3. [2022南平期中]如图,已知正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°得到△DCM.(1)求证:EF=MF.(2)当AE=1时,求EF的长.类型2 半角模型 答案 变式[2022北京海淀区模拟]在正方形ABCD中,E是CD边上一点.(1)将△ADE绕点A顺时针旋转90°得到△ABF,如图1所示,观察可知,与DE相等的线段是 ,与∠AFB相等的角是 . (2)如图2,在正方形ABCD中,P,Q分别是BC,CD边上的点,且∠PAQ=45°,猜想线段DQ,BP,PQ的数量关系,并证明.(3)在图2中,连接BD分别交AP,AQ于点M,N,请写出BM,DN,MN的数量关系,并说明理由.类型2 半角模型 答案
专项2 旋转中常见的几何模型类型1 手拉手模型1. (1)如图1,在Rt△ABC中,∠ACB=90°,AC=BC,以AC为边作等边三角形ACE,将斜边AB绕点A按逆时针方向旋转60°得到线段AP,连接PE并延长交BC于点F.则∠PFB的度数为 . (2)如果将等腰直角三角形ABC改为任意直角三角形ABC(如图2),其他条件不变,猜想∠PFB的度数,并加以证明.类型1 手拉手模型1.解:(1)60°(2)∠PFB=60°.证明如下:∵△ACE是等边三角形,∴∠CAE=∠ACE=∠AEC=60°,AE=AC.∵∠PAE=∠BAP+∠BAE=60°+∠BAE,∠BAC=∠CAE+∠BAE=60°+∠BAE,∴∠PAE=∠BAC. 由旋转可得AP=AB,∴△PAE≌△BAC,∴∠PEA=∠ACB=90°, ∴∠CEF=180°-∠PEA-∠AEC=180°-90°-60°=30°,又∠ECF=∠ACB-∠ACE=30°,∴∠PFB=∠ECF+∠CEF=30°+30°=60°.答案2. 【问题背景】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,BE,点P为DC的中点.(1)【观察猜想】观察图1,猜想线段AP与BE的数量关系是 ,位置关系是 . (2)【拓展探究】把△ADE绕点A逆时针旋转到图2的位置,(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,写出新的结论并说明理由.(3)【问题解决】把△ADE绕点A在平面内自由旋转,若DE=4,BC=8,请直接写出线段AP的取值范围.类型1 手拉手模型 答案 类型2 半角模型3. [2022南平期中]如图,已知正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°得到△DCM.(1)求证:EF=MF.(2)当AE=1时,求EF的长.类型2 半角模型 答案 变式[2022北京海淀区模拟]在正方形ABCD中,E是CD边上一点.(1)将△ADE绕点A顺时针旋转90°得到△ABF,如图1所示,观察可知,与DE相等的线段是 ,与∠AFB相等的角是 . (2)如图2,在正方形ABCD中,P,Q分别是BC,CD边上的点,且∠PAQ=45°,猜想线段DQ,BP,PQ的数量关系,并证明.(3)在图2中,连接BD分别交AP,AQ于点M,N,请写出BM,DN,MN的数量关系,并说明理由.类型2 半角模型 答案
相关资料
更多









