高考数学一轮复习课时跟踪检测01 集合的概念与运算 含解析

课时跟踪检测（一） 集合的概念与运算

一抓基础，多练小题做到眼疾手快

1．(2018·徐州、连云港、宿迁三检)已知集合A＝{x|x＝2k＋1，k∈Z}，B＝{x|0＜x＜5}，则A∩B＝________.

解析：因为集合A＝{x|x＝2k＋1，k∈Z}为奇数集，B＝{x|0＜x＜5}，所以A∩B＝{1,3}．

答案：{1,3}

2．定义：满足任意元素x∈A，则|4－x|∈A的集合称为优集，若集合A＝{1，a,7}是优集，则实数a的值为________．

解析：依题意，当x＝1时，|4－x|＝3∈A，当x＝7时，|4－x|＝3∈A，所以a＝3符合条件．

答案：3

3．(2018·如皋高三上学期调研)集合A＝{1,3}，B＝{a2＋2,3}，若A∪B＝{1,2,3}，则实数a的值为________．

解析：∵A＝{1,3}，B＝{a2＋2,3}，且A∪B＝{1,2,3}，

∴a2＋2＝2，解得a＝0，即实数a的值为0.

答案：0

4．(2018·盐城三模)已知集合A＝{1,2,3,4,5}，B＝{1,3,5,7,9}，C＝A∩B，则集合C的子集的个数为________．

解析：因为A∩B＝{1,3,5}，所以C＝{1,3,5}，故集合C的子集的个数为23＝8.

答案：8

5．(2019·徐州期中)已知集合A＝{1,2,3,4,5}，B＝{(x，y)|x∈A，y∈A，x＜y，x＋y∈A}，则集合B的子集个数是________．

解析：∵集合A＝{1,2,3,4,5}，B＝{(x，y)|x∈A，y∈A，x＜y，x＋y∈A}，

∴B＝{(1,2)，(2,3)，(1,3)，(1,4)}，

∴集合B的子集个数是24＝16.

答案：16

6．(2019·南通中学检测)已知集合A＝{x|y＝}，B＝{x|x≥a}，若A∩B＝A，则实数a的取值范围是________．

解析：因为A∩B＝A，所以A⊆B.

因为A＝{x|y＝}＝{x|9－x2≥0}＝[－3,3]，

所以[－3,3]⊆[a，＋∞)，所以a≤－3.

答案：(－∞，－3]

二保高考，全练题型做到高考达标

1．(2018·常州调研)已知{1}⊆A⊆{1,2,3}，则这样的集合A有________个．

解析：根据已知条件知符合条件的A为：A＝{1}，{1,2}，{1,3}，{1,2,3}，

∴集合A有4个．

答案：4

2．(2019·启东中学检测)已知集合A＝{x|0＜x≤6}，B＝{x∈N|2x＜33}，则集合A∩B的元素个数为________．

解析：因为A＝{x|0＜x≤6}，B＝{x∈N|2x＜33}＝{0,1,2,3,4,5}，所以A∩B＝{1,2,3,4,5}，即A∩B的元素个数为5.

答案：5

3．已知a≤1时，集合{x|a≤x≤2－a}中有且只有3个整数，则实数a的取值范围是________．

解析：因为a≤1，所以2－a≥1，所以1必在集合中．

若区间端点均为整数，则a＝0，集合中有0,1,2三个整数，所以a＝0符合题意；

若区间端点不为整数，则区间长度2＜2－2a＜4，解得－1＜a＜0，此时，集合中有0,1,2三个整数，所以－1＜a＜0符合题意．

综上，实数a的取值范围是(－1,0].

答案：(－1,0]

4．已知集合A＝{x|1≤x＜5}，B＝{x|－a＜x≤a＋3}，若B⊆(A∩B)，则实数a的取值范围为________．

解析：因为B⊆(A∩B)，所以B⊆A.

①当B＝∅时，满足B⊆A，此时－a≥a＋3，即a≤－.

②当B≠∅时，要使B⊆A，则解得－＜a≤－1.　

由①②可知，实数a的取值范围为(－∞，－1]．

答案：(－∞，－1]

5．(2018·通州中学高三测试)设U＝R，A＝(a，a＋1)，B＝[0,5)，若A⊆∁UB，则实数a的取值范围是________．

解析：因为∁UB＝(－∞，0)∪[5，＋∞)，又A⊆∁UB，所以a＋1≤0或a≥5，解得a≤－1或a≥5.

答案：(－∞，－1]∪[5，＋∞)

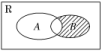6．(2019·淮阴中学检测)设全集U为实数集R，已知集合A＝，B＝{x|1≤x≤2}，则图中阴影部分所表示的集合为________．

解析：由题意知，集合A＝，阴影部分表示的集合为(∁UA)∩B＝∩{x|1≤x≤2}＝.

答案：

7．设集合A＝{x|x2－x－2≤0}，B＝{x|x＜1，且x∈Z}，则A∩B＝________.

解析：依题意得A＝{x|(x＋1)(x－2)≤0}＝{x|－1≤x≤2}，因此A∩B＝{x|－1≤x＜1，x∈Z}＝{－1,0}．

答案：{－1,0}

8．(2019·海安中学检测)已知集合M＝，N＝{y|y＝}，则(∁RM)∩N＝________.

解析：因为M＝＝(－∞，0)∪(2，＋∞)，N＝{y|y＝}＝[0，＋∞)，

所以∁RM＝[0,2]，(∁RM)∩N＝[0,2]．

答案：[0,2]

9．设全集U＝{x∈N*|x≤9}，∁U(A∪B)＝{1,3}，A∩(∁UB)＝{2,4}，则B＝________.

解析：因为全集U＝{1,2,3,4,5,6,7,8,9}，

由∁U(A∪B)＝{1,3}，

得A∪B＝{2,4,5,6,7,8,9}，

由A∩(∁UB)＝{2,4}知，{2,4}⊆A，{2,4}⊆∁UB.

所以B＝{5,6,7,8,9}．

答案：{5,6,7,8,9}

10．已知集合A＝{x|4≤2x≤16}，B＝[a，b]，若A⊆B，则实数a－b 的取值范围是________．

解析：集合A＝{x|4≤2x≤16}＝{x|22≤2x≤24}＝{x|2≤x≤4}＝[2,4]，因为A⊆B，所以a≤2，b≥4，所以a－b≤2－4＝－2，即实数a－b的取值范围是(－∞，－2]．

答案：(－∞，－2]

11．(2019·启东检测)已知集合A＝{x|a≤x≤a＋3}，B＝{x|x2＋x－6≤0}，

(1)当a＝0时，求A∪B，A∩∁RB；

(2)若A∩B＝A，求实数a的取值范围．

解：(1)当a＝0时，A＝{x|0≤x≤3}，又B＝{x|－3≤x≤2}，

所以∁RB＝{x|x＜－3或x＞2}，

所以A∪B＝{x|－3≤x≤3}，A∩∁RB＝{x|2＜x≤3}．

(2)因为A∩B＝A，所以A⊆B，

所以解得－3≤a≤－1，

所以实数a的取值范围为[－3，－1]．

12．(2018·南京高三部分学校联考)已知集合A＝{x|x2－4x－5≤0}，B＝{x|2x－6≥0}，M＝A∩B.

(1)求集合M；

(2)已知集合C＝{x|a－1≤x≤7－a，a∈R}，若M∩C＝M，求实数a的取值范围．

解：(1)由x2－4x－5≤0，得－1≤x≤5，所以A＝[－1,5]．

由2x－6≥0，得x≥3，所以B＝[3，＋∞)．

所以M＝[3,5]．

(2)因为M∩C＝M，所以M⊆C，

则解得a≤2.

故实数a的取值范围为(－∞，2]．

三上台阶，自主选做志在冲刺名校

1．已知集合A＝{x|x2－2 019x＋2 018＜0}，B＝{x|log2x＜m}，若 A⊆B，则整数m的最小值是________．

解析：由x2－2 019x＋2 018＜0，解得1＜x＜2 018，故A＝{x|1＜x＜2 018}．

由log2x＜m，解得0＜x＜2m，故B＝{x|0＜x＜2m}．由A⊆B，可得2m≥2 018，

因为210＝1 024,211＝2 048，所以整数m的最小值为11.

答案：11

2．对于集合M，定义函数fM(x)＝对于两个集合A，B，定义集合AΔB＝{x|fA(x)·fB(x)＝－1}．已知A＝{2,4,6,8,10}，B＝{1,2,4,8,12}，则用列举法写出集合AΔB＝

________.

解析：由题意知，要使fA(x)·fB(x)＝－1，必有x∈{x|x∈A且x∉B}∪{x|x∈B且x∉A}＝{1,6,10,12}，所以AΔB＝{1,6,10,12}．

答案：{1,6,10,12}

3．已知集合A＝{x|1＜x＜3}，集合B＝{x|2m＜x＜1－m}．

(1)当m＝－1时，求A∪B；

(2)若A⊆B，求实数m的取值范围；

(3)若A∩B＝∅，求实数m的取值范围．

解：(1)当m＝－1时，B＝{x|－2＜x＜2}，

则A∪B＝{x|－2＜x＜3}．

(2)由A⊆B知解得m≤－2，

即实数m的取值范围为(－∞，－2]．

(3)由A∩B＝∅，得

①若2m≥1－m，即m≥时，B＝∅，符合题意；

②若2m＜1－m，即m＜时，需或

得0≤m＜或∅，即0≤m＜.

综上知m≥0，即实数m的取值范围为[0，＋∞)．