高考数学一轮复习课时跟踪检测04 函数及其表示 含解析

课时跟踪检测（四）  函数及其表示

一抓基础，多练小题做到眼疾手快

1．(2019·淮安调研)函数f(x)＝的定义域是________．

解析：由lg(5－x2)≥0，得5－x2≥1，

即x2≤4，解得－2≤x≤2.

∴函数f(x)＝的定义域是[－2,2]．

答案：[－2,2]

2．(2018·苏州高三期中调研)函数y＝的定义域为________．

解析：由解得x＞1，且x≠2，所以函数的定义域为(1,2)∪(2，＋∞)．

答案：(1,2)∪(2，＋∞)

3．已知f＝2x－5，且f(a)＝6，则a＝________.

解析：令t＝x－1，则x＝2t＋2，f(t)＝2(2t＋2)－5＝4t－1，则4a－1＝6，解得a＝.

答案：

4．已知f(x)是一次函数，满足3f(x＋1)＝6x＋4，则f(x)＝________.

解析：设f(x)＝ax＋b(a≠0)，

则f(x＋1)＝a(x＋1)＋b＝ax＋a＋b，

依题设，3ax＋3a＋3b＝6x＋4，

∴∴

则f(x)＝2x－.

答案：2x－

5．(2019·盐城模考)已知函数f(x)＝若f(0)＝3，则f(a)＝________.

解析：因为f(0)＝3，所以a－2＝3，即a＝5，所以f(a)＝f(5)＝9.

答案：9

6．设函数f(x)＝则f(f(2))＝________，函数f(x)的值域是________．

解析：因为f(2)＝，所以f(f(2))＝f＝－.

当x＞1时，f(x)∈(0,1)，当x≤1时，f(x)∈[－3，＋∞)，

所以f(x)∈[－3，＋∞)．

答案：－　[－3，＋∞)

二保高考，全练题型做到高考达标

1．(2019·如东高级中学高三学情调研)设函数f(x)＝则f(－2)＋f(log212)＝________.

解析：因为f(－2)＝1＋log24＝3，f(log212)＝2log212－1＝6，所以f(－2)＋f(log212)＝9.

答案：9

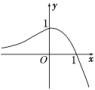2．(2018·苏州期末)函数f(x)＝的值域为________．

解析：画出f(x)的图象如图所示，可看出函数的值域为(－∞，1]．

答案：(－∞，1]

3．(2018·南京名校联考)f(x)＝则f＝________.

解析：因为f＝log3＝－2，

所以f＝f(－2)＝－2＝9.

答案：9

4．(2019·南通调研)函数f(x)＝＋lg(x＋1)的定义域是________．

解析：由题意得⇒x＞－1且x≠1，

所以函数f(x)的定义域是(－1,1)∪(1，＋∞)．

答案：(－1,1)∪(1，＋∞)

5．(2018·启东中学检测)已知函数y＝f(x2－1)的定义域为[－，]，则函数y＝f(x)的定义域为________．

解析：因为y＝f(x2－1)的定义域为[－，]，所以x∈[－，]，x2－1∈[－1,2]，所以y＝f(x)的定义域为[－1，2]．

答案：[－1,2]

6．已知具有性质：f＝－f(x)的函数，我们称为满足“倒负”变换的函数，下列函数：

①y＝x－；②y＝x＋；③y＝

其中满足“倒负”变换的函数的序号是________．

解析：对于①，f(x)＝x－，f＝－x＝－f(x)，满足；对于②，f＝＋x＝f(x)，不满足；对于③，f＝即f＝故f＝－f(x)，满足．

综上可知，满足“倒负”变换的函数是①③.

答案：①③

7．(2019·扬州一模)若函数f(x)＝为奇函数，则f(g(2))＝________.

解析：因为函数f(x)＝为奇函数，

所以当x＞0时，－x＜0，则f(－x)＝2x－2＝－f(x)，

所以f(x)＝－2x＋2，即g(x)＝－2x＋2.

所以g(2)＝－22＋2＝－2，f(g(2))＝f(－2)＝22－2＝2.

答案：2

8．已知函数f(x)＝若f(1)＝，则f(3)＝________.

解析：由f(1)＝，可得a＝，

所以f(3)＝2＝.

答案：

9．(2019·泰州一调)设函数f(x)＝若f(x)＞2，则x的取值范围是________．

解析：不等式f(x)＞2可化为或解得x＞或x＜－1.

答案：(－∞，－1)∪

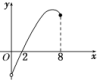10．(2019·无锡一中月考) 已知函数f(x)的图象如图所示，则函数g(x)＝logf(x)的定义域是________．

解析：要使函数g(x)有意义，需f(x)＞0，由f(x)的图象可知，当x∈(2,8]时，f(x)＞0.

答案：(2,8]

11．(2019·南京金陵中学月考)二次函数f(x)满足f(x＋1)－f(x)＝2x，且f(0)＝1.

(1)求f(x)的解析式；

(2)若在区间[－1,1]上，函数y＝f(x)的图象恒在直线y＝2x＋m的上方，试确定实数m的取值范围．

解：(1)由f(0)＝1，可设f(x)＝ax2＋bx＋1(a≠0)，故f(x＋1)－f(x)＝a(x＋1)2＋b(x＋1)＋1－(ax2＋bx＋1)＝2ax＋a＋b，由题意得解得

故f(x)＝x2－x＋1.

(2)由题意，得x2－x＋1＞2x＋m，即x2－3x＋1＞m，对x∈[－1,1]恒成立．

令g(x)＝x2－3x＋1，则问题可转化为g(x)min＞m，

又因为g(x)在[－1,1]上递减，所以g(x)min＝g(1)＝－1，

故m＜－1，即实数m的取值范围为(－∞，－1)．

12．(2018·南京期末)已知二次函数f(x)满足f(1)＝1，f(－1)＝5，且图象过原点．

(1)求二次函数f(x)的解析式；

(2)已知集合U＝[1,4]，B＝，求∁UB.

解：(1)设f(x)＝ax2＋bx＋c(a≠0)，

因为f(1)＝1，f(－1)＝5，且图象过原点，

所以解得a＝3，b＝－2，

所以f(x)＝3x2－2x.

(2)y＝＝3－，

当x∈[1,4]时，函数y＝3－是增函数，

当x＝1时，y取得最小值1；当x＝4时，y取得最大值，所以B＝，

又集合U＝[1,4]，故∁UB＝.

三上台阶，自主选做志在冲刺名校

1．已知实数a≠0，函数f(x)＝若f(1－a)＝f(1＋a)，则a＝________.

解析：当a＞0时，1－a＜1,1＋a＞1.

由f(1－a)＝f(1＋a)得2－2a＋a＝－1－a－2a，解得a＝－，不合题意；

当a＜0时，1－a＞1,1＋a＜1，

由f(1－a)＝f(1＋a)得－1＋a－2a＝2＋2a＋a，

解得a＝－，所以a的值为－.

答案：－

2．定义在R上的函数f(x)满足f(x＋2)＝2f(x)，若当0≤x≤2时，f(x)＝x(2－x)，则当－4≤x≤－2时，f(x)＝________.

解析：由题意知f(x＋4)＝2f(x＋2)＝4f(x)，当－4≤x≤－2时，0≤x＋4≤2，

所以f(x)＝f(x＋4)＝(x＋4)[2－(x＋4)]＝－(x＋4)(x＋2)，

所以当－4≤x≤－2时，f(x)＝－(x＋4)(x＋2)．

答案：－(x＋4)(x＋2)

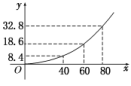3．行驶中的汽车在刹车时由于惯性作用，要继续往前滑行一段距离才能停下，这段距离叫做刹车距离．在某种路面上，某种型号汽车的刹车距离y(米)与汽车的车速x(千米/时)满足下列关系：y＝＋mx＋n(m，n是常数)．如图是根据多次实验数据绘制的刹车距离y(米)与汽车的车速x(千米/时)的关系图．

(1)求出y关于x的函数表达式；

(2)如果要求刹车距离不超过25.2米，求行驶的最大速度．

解：(1)由题意及函数图象，得

解得m＝，n＝0，

所以y＝＋(x≥0)．

(2)令＋≤25.2，

得－72≤x≤70.

因为x≥0，所以0≤x≤70.

故行驶的最大速度是70千米/时．