高考数学一轮复习课时跟踪检测06 函数的奇偶性及周期性 含解析

课时跟踪检测（六） 函数的奇偶性及周期性

一抓基础，多练小题做到眼疾手快

1．(2019·南通中学高三测试)已知函数f(x)是定义域为R的奇函数，且f(－1)＝2，那么f(0)＋f(1)＝________.

解析：因为函数f(x)是R上的奇函数，

所以f(－x)＝－f(x)，

f(1)＝－f(－1)＝－2，f(0)＝0，

所以f(0)＋f(1)＝－2.

答案：－2

2．(2018·南京三模)已知f(x)是定义在R上的偶函数，当x≥0时，f(x)＝2x－2，则不等式f(x－1)≤2的解集是________．

解析：偶函数f(x)在[0，＋∞)上单调递增，且f(2)＝2.

所以f(x－1)≤2，即f(|x－1|)≤f(2)，即|x－1|≤2，所以－1≤x≤3.

答案：[－1,3]

3．函数f(x)＝x＋＋1，f(a)＝3，则f(－a)＝________.

解析：由题意得f(a)＋f(－a)＝a＋＋1＋(－a)＋＋1＝2.

所以f(－a)＝2－f(a)＝－1.

答案：－1

4．函数f(x)在R上为奇函数，且x＞0时，f(x)＝＋1，则当x＜0时，f(x)＝________.

解析：因为f(x)为奇函数，x＞0时，f(x)＝＋1，

所以当x＜0时，－x＞0，

f(x)＝－f(－x)＝－(＋1)，

即x＜0时，f(x)＝－(＋1)＝－－1.

答案：－－1

5．(2019·连云港高三测试)已知函数f(x)是定义在R上的奇函数，且当x＞0时，f(x)＝

x，则f(－2＋log35)＝________.

解析：由f(x)是定义在R上的奇函数，得f(－2＋log35)＝－f(2－log35)，

由于当x＞0时，f(x)＝x，

故f(－2＋log35)＝－f＝－＝－.

答案：－

6．(2018·南通一调)若函数f(x)＝(a，b∈R)为奇函数，则f(a＋b)＝________.

解析：法一：因为函数f(x)为奇函数，

所以即

解得经验证a＝－1，b＝2满足题设条件，

所以f(a＋b)＝f(1)＝－1.

法二：因为函数f(x)为奇函数，所以f(x)的图象关于原点对称，由题意知，

当x≥0，二次函数的图象顶点坐标为，

当x＜0，二次函数的图象顶点坐标为(－1，－a)，

所以解得a＝－1，b＝2，

经验证a＝－1，b＝2满足题设条件，

所以f(a＋b)＝f(1)＝－1.

答案：－1

二保高考，全练题型做到高考达标

1．(2018·抚顺期末)设f(x)是定义在[－2b,3＋b]上的偶函数，且在[－2b,0]上为增函数，则f(x－1)≥f(3)的解集为________．

解析：∵f(x)是定义在[－2b,3＋b]上的偶函数，

∴－2b＋3＋b＝0，

∴b＝3，

∴f(x)是定义在[－6,6]上的偶函数，且在[－6,0]上为增函数，

∴f(x)在[0,6]上为减函数，

∴由f(x－1)≥f(3)，得|x－1|≤3，

解得－2≤x≤4，

∴f(x－1)≥f(3)的解集为{x|－2≤x≤4}．

答案：{x|－2≤x≤4}

2．(2019·常州一中模拟)设定义在R上的偶函数f(x)满足f(x＋1)＋f(x)＝1，且当x∈[1,2]时，f(x)＝2－x，则f(－2 018.5)＝________.

解析：由f(x＋1)＋f(x)＝1在R上恒成立，得f(x－1)＋f(x)＝1，两式相减得f(x＋1)－f(x－1)＝0，即f(x＋1)＝f(x－1)恒成立，故函数f(x)的周期是2，

∴f(－2 018.5)＝f(－0.5)＝f(1.5)，

又当x∈[1,2]时，f(x)＝2－x，

∴f(－2 018.5)＝f(1.5)＝2－1.5＝0.5.

答案：0.5

3．已知函数f(x)是定义在[－2,2]上的奇函数，且在区间[0,2]上是单调减函数．若f(2x＋1)＋f(1)＜0，则x的取值范围是________．

解析：∵函数f(x)是定义在[－2,2]上的奇函数，且在区间[0,2]上是单调减函数，

∴函数f(x)在区间[－2,2]上是单调减函数．

∵f(2x＋1)＋f(1)＜0，即f(2x＋1)＜－f(1)，

∴f(2x＋1)＜f(－1)．

则解得－1＜x≤.

∴x的取值范围是.

答案：

4．(2018·泰州期末)设f(x)是R上的奇函数，当x＞0时，f(x)＝2x＋ln，记an＝f(n－5)，则数列{an}的前8项和为________．

解析：数列{an}的前8项和为f(－4)＋f(－3)＋…＋f(3)＝f(－4)＋(f(－3)＋f(3))＋(f(－2)＋f(2))＋(f(－1)＋f(1))＋f(0)＝f(－4)＝－f(4)＝－＝－16.

答案：－16

5．(2018·徐州期中)已知函数f(x)＝ex－e－x＋1(e为自然对数的底数)，若f(2x－1)＋f(4－x2)＞2，则实数x的取值范围为________．

解析：令g(x)＝f(x)－1＝ex－e－x，则g(x)为奇函数，且在R上单调递增．因为f(2x－1)＋f(4－x2)＞2，所以f(2x－1)－1＋f(4－x2)－1＞0，即g(2x－1)＋g(4－x2)＞0，所以g(2x－1)＞g(x2－4)，即2x－1＞x2－4，解得x∈(－1,3)．

答案：(－1,3)

6．(2019·镇江中学测试)已知奇函数f(x)在定义域R上是单调减函数，若实数a满足f(2|2a－1|)＋f(－2)＞0，则a的取值范围是________．

解析：由f(2|2a－1|)＋f(－2)＞0，可得f(2|2a－1|)＞－f(－2)．因为f(x)为奇函数，所以f(2|2a－1|)＞f(2)．因为f(x)在定义域R上是单调减函数，所以2|2a－1|＜2，即|2a－1|＜，解得－＜a＜.

答案：

7．(2019·苏州调研)已知奇函数f(x)在(－∞，0)上单调递减，且f(2)＝0，则不等式＞0的解集为________．

解析：由＞0，可得或因为奇函数f(x)在(－∞，0)上单调递减，所以f(x)在(0，＋∞)上单调递减，且f(2)＝f(－2)＝0，所以当x＞1时，f(x)＞0的解集为(1,2)；当x＜1时，f(x)＜0的解集为(－2,0)．

所以不等式＞0的解集为(－2,0)∪(1,2)．

答案：(－2,0)∪(1,2)

8．函数f(x)在R上满足f(－x)＝－f(x)，当x≥0时，f(x)＝－ex＋1＋mcos(π＋x)，记a＝－πf(－π)，b＝－·f，c＝ef(e)，则a，b，c的大小关系为________．

解析：∵函数f(x)为R上的奇函数，且当x≥0时，f(x)＝－ex＋1＋mcos(π＋x)，

∴f(0)＝－1＋1－m＝0，即m＝0，

∴f(x)＝－ex＋1(x≥0)．

令g(x)＝xf(x)，

有g(－x)＝(－x)f(－x)＝xf(x)＝g(x)，

∴函数g(x)为偶函数，

当x≥0时，g(x)＝xf(x)＝x(1－ex)，g′(x)＝f(x)＋xf′(x)＝1－(1＋x)ex＜0，

∴函数g(x)在[0，＋∞)上为减函数，

∵a＝－πf(－π)＝g(－π)＝g(π)，b＝－f＝g＝g，c＝ef(e)＝g(e)，

又e＜π＜，∴b＜a＜c.

答案：b＜a＜c

9．已知函数f(x)＝是奇函数．

(1)求实数m的值；

(2)若函数f(x)在区间[－1，a－2]上单调递增，求实数a的取值范围．

解：(1)设x＜0，则－x＞0，

所以f(－x)＝－(－x)2＋2(－x)＝－x2－2x.

又f(x)为奇函数，所以f(－x)＝－f(x)，

于是x＜0时，f(x)＝x2＋2x＝x2＋mx，所以m＝2.

(2)要使f(x)在[－1，a－2]上单调递增，

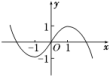
结合f(x)的图象(如图所示)知

所以1＜a≤3，故实数a的取值范围是(1,3]．

10．(2018·大同期末)已知函数f(x)＝loga(x＋1)，g(x)＝loga(1－x)，其中a＞0，a≠1.

(1)求函数F(x)＝f(x)－g(x)的定义域；

(2)判断F(x)＝f(x)－g(x)的奇偶性，并说明理由；

(3)当a＞1时，求使F(x)＞0成立的x的取值范围．

解：(1)∵F(x)＝f(x)－g(x)＝loga(x＋1)－loga(1－x)，

∴解得－1＜x＜1，

∴函数F(x)的定义域为(－1,1)．

(2)F(x)为(－1,1)上的奇函数．理由如下：

由(1)知F(x)的定义域为(－1,1)，关于原点对称，F(－x)＝loga(－x＋1)－loga(1＋x)＝－[loga(x＋1)－loga(1－x)]＝－F(x)，

∴函数F(x)为(－1,1)上的奇函数．

(3)根据题意，F(x)＝loga(x＋1)－loga(1－x)，

当a＞1时，由F(x)＞0，得loga(x＋1)＞loga(1－x)，

即

解得0＜x＜1，

故x的取值范围为(0,1)．

三上台阶，自主选做志在冲刺名校

1．(2019·南通模拟)已知定义在R上的奇函数y＝f(x)满足f(2＋x)＝f(2－x)，当－2≤x＜0时，f(x)＝2x，若an＝f(n)(n∈N*)，则a2 018＝________.

解析：∵f(2＋x)＝f(2－x)，以2＋x代替上式中的x，得f(4＋x)＝f(－x)，

又函数y＝f(x)是定义在R上的奇函数，

∴f(－x)＝－f(x)，

∴f(4＋x)＝f(－x)＝－f(x)，

再以4＋x代替上式中的x，得f(8＋x)＝－f(4＋x)＝f(x)，∴函数f(x)的周期为8.

∴a2 018＝f(2 018)＝f(252×8＋2)＝f(2)，

而f(2)＝－f(－2)＝－，

∴a2 018＝－.

答案：－

2．设函数f(x)是定义在R上的奇函数，对任意实数x有f＝－f成立．

(1)证明y＝f(x)是周期函数，并指出其周期；

(2)若f(1)＝2，求f(2)＋f(3)的值；

(3)若g(x)＝x2＋ax＋3，且y＝|f(x)|·g(x)是偶函数，求实数a的值．

解：(1)由f ＝－f ，

且f(－x)＝－f(x)，知f(3＋x)＝f ＝

－f ＝－f(－x)＝f(x)，

所以y＝f(x)是周期函数，且T＝3是其一个周期．

(2)因为f(x)为定义在R上的奇函数，所以f(0)＝0，

且f(－1)＝－f(1)＝－2，又T＝3是y＝f(x)的一个周期，所以f(2)＋f(3)＝f(－1)＋f(0)＝－2＋0＝－2.

(3)因为y＝|f(x)|·g(x)是偶函数，

且|f(－x)|＝|－f(x)|＝|f(x)|，所以|f(x)|为偶函数．

故g(x)＝x2＋ax＋3为偶函数，

即g(－x)＝g(x)恒成立，

于是(－x)2＋a(－x)＋3＝x2＋ax＋3恒成立．

于是2ax＝0恒成立，所以a＝0.