初中27.2.2 相似三角形的性质同步训练题

相似三角形的周长和面积

1、在△ABC中，∠BAC=，AD⊥BC于D，BD=3，AD=9，则CD=      ，AB：AC=        。

2、直角三角形的两条直角边分别为，则它的斜边上的高与斜边之比为     。

3、若△ABC∽△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2,且AB=12cm,则DE=     cm

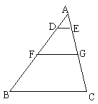4、如图,ΔABC中,DE∥FG∥BC,AD∶DF∶FB=1∶2∶3,则S四边形DFGE∶S四边形FBCG=

_________.

5、等腰三角形ABC和DEF相似，其相似比为3：4，则它们底边上对应高线的比为（   ）

A、3：4         B、4：3        C、1：2          D、2：1

6、如图，这是圆桌正上方的灯泡（看作一个点）发出的光线照射到桌面后在地面上形成（圆形）的示意图. 已知桌面直径为1.2米，桌面离地面1米. 若灯泡离地面3米，则地面上阴影部分的面积为                                                                                                                                            （   -）

A.、0.36米2   B、0.81米2     C、2米2           D、3.24米2

7、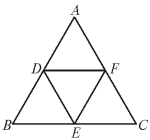如图，分别取等边三角形ABC各边的中点D、E、F，得△DEF.若△ABC的边长为a.

（1）△DEF与△ABC相似吗？如果相似，相似比是多少？

（2）分别求出这两个三角形的面积.

（3）这两个三角形的面积比与边长之比有什么关系吗？

8、如图，在ΔABC中，BA=BC=20cm，AC=30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x。（1）当x为何值时，PQ∥BC？（2）当，求的值；

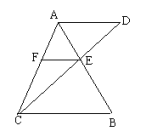9、在△ABC中，AE∶EB=1 ∶2，EF∥BC，AD∥BC交CE的延长线于D，求S△AEF∶S△BCE的值。

10、如图，△ABC是一块锐角三角形余料，边BC=120mm， 高AD=80mm， 要把它加工成矩形零件，使一边在BC上，其余两个顶点分别在边AB、AC上，

（1）若这个矩形是正方形，那么边长是多少？

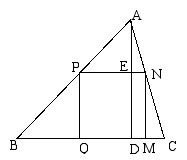（2）若这个矩形的长是宽的2倍，则边长是多少？

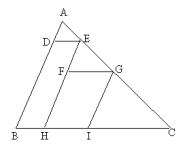
11、如图,在△ABC中,DE∥FG∥BC，GI∥EF∥AB，若△ADE、△EFG、△GIC的面积分别为20cm2、45cm2、80cm2，求△ABC的面积。

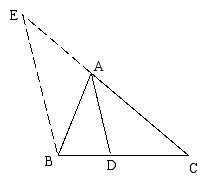
12、有人猜想三角形内角平分线有这样一个性质:如图,在△ABC中,AD平分∠BAC,则.如果你认为这个猜想是正确的,请写出一个完整的推理过程(利用图中辅助线：作BE//AD交CA延长线于E)说明这个猜想的正确性; 如果你认为这个猜想不正确,也请说明理由.