数学九年级下册27.3 位似学案

这是一份数学九年级下册27.3 位似学案，共7页。学案主要包含了教学目标，重点，新知探究，典型例题，教学反思等内容，欢迎下载使用。
             平面直角坐标系中的位似                                                              一、教学目标1．巩固位似图形及其有关概念．2．会用图形的坐标的变化来表示图形的位似变换，掌握把一个图形按一定大小比例放大或缩小后，点的坐标变化的规律． 二、重点、难点1．重点：用图形的坐标的变化来表示图形的位似变换．2．难点：把一个图形按一定大小比例放大或缩小后，点的坐标变化的规律． 三、新知探究1. 在平面直角坐标系中有两点A（6，3），B（6，0），以原点O为位似中心， 相似比为1：3，把线段AB缩小.      方法一：                              方法二：   探究：（1）在方法一中，A’的坐标是        ，B’的坐标是        ，对应点坐标之比是　　　；（2）在方法二中，A’’的坐标是        ，B’’的坐标是        ，对应点坐标之比是　　　 归纳：在平面直角坐标系中，如果位似变换是以原点为位似中心，新图形与原图形的相似比为k，那么原图形上的点（x、y) 对应的位似图形上的点的坐标为（        )或（        )。 四、典型例题例1. 如图表示△AOB和把它缩小后得到的△COD，求△COD和△AOB的相似比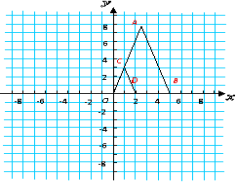．       例2. 如图，△ABC三个顶点坐标分别为A（2，－2），B（4，－5），C（5，－2），以原点O为位似中心，将这个三角形放大为原来的2倍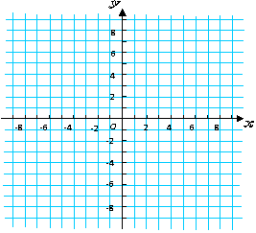．         例3．（教材P50）如图所示的图案中，你能找出平移、轴对称、旋转和位似这些变换吗？      •                    课堂检测                如图，在平面直角坐标系中，以原点为位似中心，将△AOB扩大到原来的2倍，得到△OA′B′.若点A的坐标是(1，2)，则点A′的坐标是(　　)   A．(2，4)    B．(－1，－2)      C．(－2，－4)   D．(－2，－1) 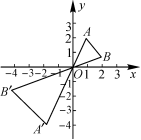               如图，线段AB两个端点的坐标分别为A(6，6)，B(8，2)，以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C的坐标为(　　)   (3，3)  B．(4，3)  C．(3，1)  D．(4，1)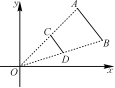3．在平面直角坐标系中，已知点E(－4，2)，F(－2，－2)，以原点O为位似中心，相似比为，把△EFO缩小，则点E的对应点E′的坐标是(　　)  A．(－2，1)   B．(－8，4)   C．(－8，4)或(8，－4)   D．(－2，1)或(2，－1)  4.某个图形上各点的横、纵坐标都变成原来的，连接各点所得图形与原图形相比(    )  A.完全没有变化                   B.扩大成原来的2倍  C.面积缩小为原来的             D.关于纵轴成轴对称 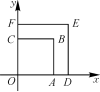 5．如图，正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为1∶，点A的坐标为(1，0)，则E点的坐标为(　　)   A．(，0)     B．(，)   C．(，)    D．(2，2) 6、如图，四边形ABCD的坐标分别为A（－6，6），B（－8，2），C（－4，0），D（－2，4），画出它的一个以原点O为位似中心，相似比为的位似图形． 六、教学反思