高考数学一轮复习课时作业：8 指数与指数函数 Word版含解析

这是一份高考数学一轮复习课时作业：8 指数与指数函数 Word版含解析，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
课时作业8　指数与指数函数一、选择题1．化简4a·b÷的结果为(　C　)A．－   B．－C．－   D．－6ab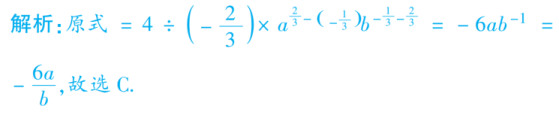2．设函数f(x)＝若f(a)<1，则实数a的取值范围是(　C　)A．(－∞，－3)   B．(1，＋∞)C．(－3,1)   D．(－∞，－3)∪(1，＋∞)解析：当a<0时，不等式f(a)<1为a－7<1，即a<8，即a<－3，因为0<<1，所以a>－3，此时－3<a<0；当a≥0时，不等式f(a)<1为<1，所以0≤a<1.故a的取值范围是(－3,1)，故选C.3．(2019·湖南永州模拟)下列函数中，与函数y＝2x－2－x的定义域、单调性与奇偶性均一致的是(　B　)A．y＝sinx   B．y＝x3C．y＝x   D．y＝log2x解析：y＝2x－2－x是定义域为R的单调递增函数，且是奇函数．而y＝sinx不是单调递增函数，不符合题意；y＝x是非奇非偶函数，不符合题意；y＝log2x的定义域是(0，＋∞)，不符合题意；y＝x3是定义域为R的单调递增函数，且是奇函数符合题意．故选B.4．二次函数y＝－x2－4x(x>－2)与指数函数y＝x的图象的交点个数是(　C　)A．3   B．2C．1   D．0解析：因为函数y＝－x2－4x＝－(x＋2)2＋4(x>－2)，且当x＝－2时，y＝－x2－4x＝4，y＝x＝4，则在同一直角坐标系中画出y＝－x2－4x(x>－2)与y＝x的图象如图所示，由图象可得，两个函数图象的交点个数是1，故选C.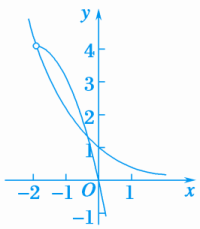5．(2019·福建厦门一模)已知a＝0.3，b＝log0.3，c＝ab，则a，b，c的大小关系是(　B　)A．a<b<c   B．c<a<bC．a<c<b   D．b<c<a解析：b＝log0.3>log＝1>a＝0.3，c＝ab<a.∴c<a<b.故选B.6．已知a，b∈(0,1)∪(1，＋∞)，当x>0时，1<bx<ax，则(　C　)A．0<b<a<1   B．0<a<b<1C．1<b<a   D．1<a<b解析：∵当x>0时，1<bx，∴b>1.∵当x>0时，bx<ax，∴当x>0时，x>1.∴>1，∴a>b.∴1<b<a，故选C.7.如图，在面积为8的平行四边形OABC中，AC⊥CO，AC与BO交于点E.若指数函数y＝ax(a>0，且a≠1)经过点E，B，则a的值为(　A　)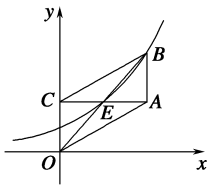A.   B.C．2   D．3解析：设点E(t，at)，则点B的坐标为(2t,2at)．因为2at＝a2t，所以at＝2.因为平行四边形OABC的面积＝OC×AC＝at×2t＝4t，又平行四边形OABC的面积为8，所以4t＝8，t＝2，所以a2＝2，a＝.故选A.二、填空题8．不等式2x2－x<4的解集为{x|－1<x<2}．解析：∵2x2－x<4，∴2x2－x<22，∴x2－x<2，即x2－x－2<0，解得－1<x<2.9．若直线y1＝2a与函数y2＝|ax－1|(a>0且a≠1)的图象有两个公共点，则a的取值范围是.解析：(数形结合法)当0<a<1时，作出函数y2＝|ax－1|的图象，由图象可知0<2a<1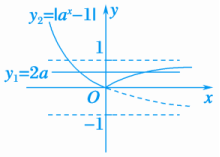，∴0<a<；同理，当a>1时，解得0<a<，与a>1矛盾．综上，a的取值范围是.10．已知函数f(x)＝2x－，函数g(x)＝则函数g(x)的最小值是0.解析：当x≥0时，g(x)＝f(x)＝2x－为单调增函数，所以g(x)≥g(0)＝0；当x<0时，g(x)＝f(－x)＝2－x－为单调减函数，所以g(x)>g(0)＝0，所以函数g(x)的最小值是0.11．(2019·湖南益阳调研)已知函数f(x)＝(a∈R)的图象关于点对称，则a＝1.解析：由已知，得f(x)＋f(－x)＝1，即＋＝1，整理得(a－1)[22x＋(a－1)·2x＋1]＝0，所以当a－1＝0，即a＝1时，等式成立．三、解答题12．设a>0，且a≠1，函数y＝a2x＋2ax－1在[－1,1]上的最大值是14，求实数a的值．解：令t＝ax(a>0，且a≠1)，则原函数化为y＝f(t)＝(t＋1)2－2(t>0)．①当0<a<1，x∈[－1,1]时，t＝ax∈，此时f(t)在上为增函数．所以f(t)max＝f＝2－2＝14.所以2＝16，解得a＝－(舍去)或a＝.②当a>1时，x∈[－1,1]，t＝ax∈，此时f(t)在上是增函数．所以f(t)max＝f(a)＝(a＋1)2－2＝14，解得a＝3或a＝－5(舍去)．综上得a＝或3.13．(2019·河南八市第一次测评)设函数f(x)＝x2－a与g(x)＝ax(a>1且a≠2)在区间(0，＋∞)上具有不同的单调性，则M＝(a－1)0.2与N＝0.1的大小关系是(　D　)A．M＝N   B．M≤NC．M<N   D．M>N解析：因为f(x)＝x2－a与g(x)＝ax(a>1且a≠2)在区间(0，＋∞)上具有不同的单调性，所以a>2，所以M＝(a－1)0.2>1，N＝0.1<1，所以M>N，故选D.14．已知函数f(x)＝1－(a>0，a≠1)且f(0)＝0.(1)求a的值；(2)若函数g(x)＝(2x＋1)·f(x)＋k有零点，求实数k的取值范围；(3)当x∈(0,1)时，f(x)>m·2x－2恒成立，求实数m的取值范围．解：(1)对于函数f(x)＝1－(a>0，a≠1)，由f(0)＝1－＝0，得a＝2.(2)由(1)知f(x)＝1－＝1－.因为函数g(x)＝(2x＋1)·f(x)＋k＝2x＋1－2＋k＝2x－1＋k有零点，所以函数y＝2x的图象和直线y＝1－k有交点，∴1－k>0，即k<1.(3)∵当x∈(0,1)时，f(x)>m·2x－2恒成立，即1－>m·2x－2恒成立，亦即m<－恒成立，令t＝2x，则t∈(1,2)，且m<－＝＝＋.由于y＝＋在t∈(1,2)上单调递减，∴＋>＋＝，∴m≤.15．已知实数a，b满足>a>b>，则(　B　)A．b<2   B．b>2C．a<   D．a>解析：由>a，得a>1，由a>b，得2a>b，故2a<b，由b>，得b>4，得b<4.由2a<b，得b>2a>2，a<<2，∴1<a<2,2<b<4.对于选项A，B，由于b2－4(b－a)＝(b－2)2＋4(a－1)>0恒成立，故A错误，B正确；对于选项C，D，a2－(b－a)＝a＋2－，由于1<a<2,2<b<4，故该式的符号不确定，故C，D错误．故选B.16．已知max(a，b)表示a，b两数中的最大值．若f(x)＝max(e|x|，e|x－2|)，则f(x)的最小值为e.解析：由题意得，f(x)＝当x≥1时，f(x)＝ex≥e(当x＝1时取等号)，当x<1时，f(x)＝e|x－2|＝e2－x>e，因此x＝1时，f(x)有最小值f(1)＝e.