


所属成套资源:高考数学一轮复习课时作业 含解析
高考数学一轮复习课时作业:11 函数与方程 Word版含解析
展开
这是一份高考数学一轮复习课时作业:11 函数与方程 Word版含解析,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
![]() 课时作业11 函数与方程
课时作业11 函数与方程![]() 一、选择题1.函数f(x)=的零点个数是( D )A.0 B.1C.2 D.3解析:当x>0时,令f(x)=0可得x=1;当x≤0时,令f(x)=0可得x=-2或x=0.因此函数的零点个数为3.故选D.2.方程ln(x+1)-=0(x>0)的根存在的大致区间是( B )A.(0,1) B.(1,2)C.(2,e) D.(3,4)解析:令f(x)=ln(x+1)-,则f(1)=ln(1+1)-2=ln2-2<0,f(2)=ln3-1>0,所以函数f(x)的零点所在大致区间为(1,2).故选B.3.已知函数f(x)=log3-a在区间(1,2)内有零点,则实数a的取值范围是( C )A.(-1,-log32) B.(0,log52)C.(log32,1) D.(1,log34)解析:∵单调函数f(x)=log3-a在区间(1,2)内有零点,∴f(1)·f(2)<0,即(1-a)·(log32-a)<0,解得log32<a<1,故选C.4.关于x的方程|x2-2x|=a2+1(a>0)的解的个数是( B )A.1 B.2 C.3 D.4解析:∵a>0,∴a2+1>1.而y=|x2-2x|的图象如图所示,∴y=|x2-2x|的图象与y=a2+1的图象总有2个交点,即方程|x2-2x|=a2+1(a>0)的解的个数是2.
一、选择题1.函数f(x)=的零点个数是( D )A.0 B.1C.2 D.3解析:当x>0时,令f(x)=0可得x=1;当x≤0时,令f(x)=0可得x=-2或x=0.因此函数的零点个数为3.故选D.2.方程ln(x+1)-=0(x>0)的根存在的大致区间是( B )A.(0,1) B.(1,2)C.(2,e) D.(3,4)解析:令f(x)=ln(x+1)-,则f(1)=ln(1+1)-2=ln2-2<0,f(2)=ln3-1>0,所以函数f(x)的零点所在大致区间为(1,2).故选B.3.已知函数f(x)=log3-a在区间(1,2)内有零点,则实数a的取值范围是( C )A.(-1,-log32) B.(0,log52)C.(log32,1) D.(1,log34)解析:∵单调函数f(x)=log3-a在区间(1,2)内有零点,∴f(1)·f(2)<0,即(1-a)·(log32-a)<0,解得log32<a<1,故选C.4.关于x的方程|x2-2x|=a2+1(a>0)的解的个数是( B )A.1 B.2 C.3 D.4解析:∵a>0,∴a2+1>1.而y=|x2-2x|的图象如图所示,∴y=|x2-2x|的图象与y=a2+1的图象总有2个交点,即方程|x2-2x|=a2+1(a>0)的解的个数是2.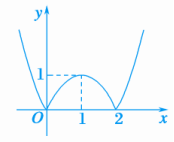 5.(2019·广东七校联合体联考)若函数f(x)=2x+a2x-2a的零点在区间(0,1)上,则实数a的取值范围是( C )A. B.(-∞,1)C. D.(1,+∞)解析:易知函数f(x)的图象连续,且在(0,1)上单调递增.∴f(0)f(1)=(1-2a)(2+a2-2a)<0,解得a>.6.已知函数f(x)=lnx-ax2+ax恰有两个零点,则实数a的取值范围为( C )A.(-∞,0) B.(0,+∞)C.(0,1)∪(1,+∞) D.(-∞,0)∪{1}解析:由题意,显然x=1是函数f(x)的一个零点,取a=-1,则f(x)=lnx+x2-x,f′(x)==>0恒成立.则f(x)仅有一个零点,不符合题意,排除A、D;取a=1,则f(x)=lnx-x2+x,f′(x)==,f′(x)=0得x=1,则f(x)在(0,1)上递增,在(1,+∞)上递减,f(x)max=f(1)=0,即f(x)仅有一个零点,不符合题意,排除B,故选C.二、填空题7.已知f(x)=则函数g(x)=f(x)-ex的零点个数为2.解析:函数g(x)=f(x)-ex的零点个数即为函数y=f(x)与y=ex的图象的交点个数.作出函数图象可知有2个交点,即函数g(x)=f(x)-ex有2个零点.
5.(2019·广东七校联合体联考)若函数f(x)=2x+a2x-2a的零点在区间(0,1)上,则实数a的取值范围是( C )A. B.(-∞,1)C. D.(1,+∞)解析:易知函数f(x)的图象连续,且在(0,1)上单调递增.∴f(0)f(1)=(1-2a)(2+a2-2a)<0,解得a>.6.已知函数f(x)=lnx-ax2+ax恰有两个零点,则实数a的取值范围为( C )A.(-∞,0) B.(0,+∞)C.(0,1)∪(1,+∞) D.(-∞,0)∪{1}解析:由题意,显然x=1是函数f(x)的一个零点,取a=-1,则f(x)=lnx+x2-x,f′(x)==>0恒成立.则f(x)仅有一个零点,不符合题意,排除A、D;取a=1,则f(x)=lnx-x2+x,f′(x)==,f′(x)=0得x=1,则f(x)在(0,1)上递增,在(1,+∞)上递减,f(x)max=f(1)=0,即f(x)仅有一个零点,不符合题意,排除B,故选C.二、填空题7.已知f(x)=则函数g(x)=f(x)-ex的零点个数为2.解析:函数g(x)=f(x)-ex的零点个数即为函数y=f(x)与y=ex的图象的交点个数.作出函数图象可知有2个交点,即函数g(x)=f(x)-ex有2个零点.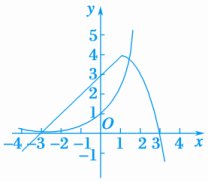 8.若函数f(x)=x2+ax+b的两个零点是-2和3,则不等式af(-2x)>0的解集是.解析:∵f(x)=x2+ax+b的两个零点是-2,3.∴-2,3是方程x2+ax+b=0的两根,由根与系数的关系知∴∴f(x)=x2-x-6.∵不等式af(-2x)>0,即-(4x2+2x-6)>0⇔2x2+x-3<0,解集为.9.已知函数f(x)=则函数f(x)的零点个数为3.解析:解法1:当x>1时,由log2(x-1)=0得x=2,即x=2为函数f(x)在区间(1,+∞)上的一个零点;当x≤1时,∵f(x)=x3-3x+1,∴f′(x)=3x2-3,由f′(x)=0得x=-1或x=1,∵当x<-1时,f′(x)>0,当-1≤x≤1时,f′(x)≤0,∴x=-1为函数f(x)=x3-3x+1在(-∞,1]上的极大值点,∵f(-1)=3>0,f(1)=-1<0,且当x→-∞时,f(x)→-∞,∴函数f(x)=x3-3x+1在(-∞,1]上有两个不同的零点.综上,函数f(x)的零点个数为3.解法2:当x>1时,作出函数y=log2(x-1)的图象如图1所示,当x≤1时,由f(x)=x3-3x+1=0得,x3=3x-1,在同一个平面直角坐标系中分别作出函数y=x3和y=3x-1的图象如图2所示,由图1,2可知函数f(x)的零点个数为3.
8.若函数f(x)=x2+ax+b的两个零点是-2和3,则不等式af(-2x)>0的解集是.解析:∵f(x)=x2+ax+b的两个零点是-2,3.∴-2,3是方程x2+ax+b=0的两根,由根与系数的关系知∴∴f(x)=x2-x-6.∵不等式af(-2x)>0,即-(4x2+2x-6)>0⇔2x2+x-3<0,解集为.9.已知函数f(x)=则函数f(x)的零点个数为3.解析:解法1:当x>1时,由log2(x-1)=0得x=2,即x=2为函数f(x)在区间(1,+∞)上的一个零点;当x≤1时,∵f(x)=x3-3x+1,∴f′(x)=3x2-3,由f′(x)=0得x=-1或x=1,∵当x<-1时,f′(x)>0,当-1≤x≤1时,f′(x)≤0,∴x=-1为函数f(x)=x3-3x+1在(-∞,1]上的极大值点,∵f(-1)=3>0,f(1)=-1<0,且当x→-∞时,f(x)→-∞,∴函数f(x)=x3-3x+1在(-∞,1]上有两个不同的零点.综上,函数f(x)的零点个数为3.解法2:当x>1时,作出函数y=log2(x-1)的图象如图1所示,当x≤1时,由f(x)=x3-3x+1=0得,x3=3x-1,在同一个平面直角坐标系中分别作出函数y=x3和y=3x-1的图象如图2所示,由图1,2可知函数f(x)的零点个数为3.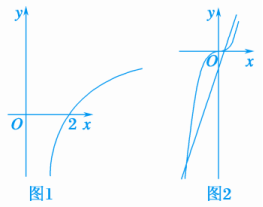 10.定义在R上的奇函数f(x)满足:当x>0时,f(x)=2 015x+log2 015x,则在R上,函数f(x)零点的个数为3.解析:因为函数f(x)为R上的奇函数,所以f(0)=0,当x>0时,f(x)=2 015x+log2 015x在区间内存在一个零点,又f(x)为增函数,因此在(0,+∞)内有且仅有一个零点.根据对称性可知函数在(-∞,0)内有且仅有一个零点,从而函数f(x)在R上的零点个数为3.三、解答题11.已知函数f(x)=x3-x2++.证明:存在x0∈,使f(x0)=x0.证明:令g(x)=f(x)-x.∵g(0)=,g=f-=-,∴g(0)·g<0.又函数g(x)在上是连续曲线,∴存在x0∈,使g(x0)=0,即f(x0)=x0.12.已知a是正实数,函数f(x)=2ax2+2x-3-a.如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围.解:f(x)=2ax2+2x-3-a的对称轴为x=-.①当-≤-1,即0<a≤时,须使即∴无解.②当-1<-<0,即a>时,须使即解得a≥1,∴a的取值范围是[1,+∞).
10.定义在R上的奇函数f(x)满足:当x>0时,f(x)=2 015x+log2 015x,则在R上,函数f(x)零点的个数为3.解析:因为函数f(x)为R上的奇函数,所以f(0)=0,当x>0时,f(x)=2 015x+log2 015x在区间内存在一个零点,又f(x)为增函数,因此在(0,+∞)内有且仅有一个零点.根据对称性可知函数在(-∞,0)内有且仅有一个零点,从而函数f(x)在R上的零点个数为3.三、解答题11.已知函数f(x)=x3-x2++.证明:存在x0∈,使f(x0)=x0.证明:令g(x)=f(x)-x.∵g(0)=,g=f-=-,∴g(0)·g<0.又函数g(x)在上是连续曲线,∴存在x0∈,使g(x0)=0,即f(x0)=x0.12.已知a是正实数,函数f(x)=2ax2+2x-3-a.如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围.解:f(x)=2ax2+2x-3-a的对称轴为x=-.①当-≤-1,即0<a≤时,须使即∴无解.②当-1<-<0,即a>时,须使即解得a≥1,∴a的取值范围是[1,+∞).![]() 13.(2019·惠州市调研考试)函数f(x)是定义在R上的奇函数,当x>0时,f(x)=则函数g(x)=xf(x)-1在[-6,+∞)上的所有零点之和为( A )A.8 B.32C. D.0解析:令g(x)=xf(x)-1=0,则x≠0,所以函数g(x)的零点之和等价于函数y=f(x)的图象和y=的图象的交点的横坐标之和,分别作出x>0时,y=f(x)和y=的大致图象,如图所示,
13.(2019·惠州市调研考试)函数f(x)是定义在R上的奇函数,当x>0时,f(x)=则函数g(x)=xf(x)-1在[-6,+∞)上的所有零点之和为( A )A.8 B.32C. D.0解析:令g(x)=xf(x)-1=0,则x≠0,所以函数g(x)的零点之和等价于函数y=f(x)的图象和y=的图象的交点的横坐标之和,分别作出x>0时,y=f(x)和y=的大致图象,如图所示,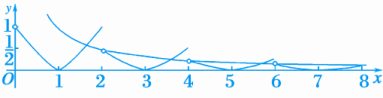 由于y=f(x)和y=的图象都关于原点对称,因此函数g(x)在[-6,6]上的所有零点之和为0,而当x=8时,f(x)=,即两函数的图象刚好有1个交点,且当x∈(8,+∞)时,y=的图象都在y=f(x)的图象的上方,因此g(x)在[-6,+∞)上的所有零点之和为8.故选A.14.已知关于x的方程|2x-10|=a有两个不同的实根x1,x2,且x2=2x1,则实数a=6.
由于y=f(x)和y=的图象都关于原点对称,因此函数g(x)在[-6,6]上的所有零点之和为0,而当x=8时,f(x)=,即两函数的图象刚好有1个交点,且当x∈(8,+∞)时,y=的图象都在y=f(x)的图象的上方,因此g(x)在[-6,+∞)上的所有零点之和为8.故选A.14.已知关于x的方程|2x-10|=a有两个不同的实根x1,x2,且x2=2x1,则实数a=6.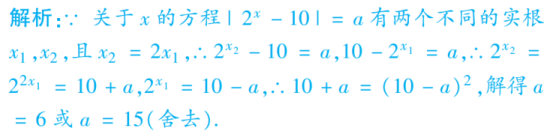 15.(2019·福州四校联考)已知函数f(x)=若F(x)=f[f(x)+1]+m有两个零点x1,x2,则x1·x2的取值范围是( D )A.[4-2ln2,+∞) B.(,+∞)C.(-∞,4-2ln2] D.(-∞,)
15.(2019·福州四校联考)已知函数f(x)=若F(x)=f[f(x)+1]+m有两个零点x1,x2,则x1·x2的取值范围是( D )A.[4-2ln2,+∞) B.(,+∞)C.(-∞,4-2ln2] D.(-∞,) 16.(2019·德州模拟)已知函数f(x)=-x2-2x.g(x)=(1)求g[f(1)]的值;(2)若方程g[f(x)]-a=0有4个实数根,求实数a的取值范围.解:(1)∵f(1)=-12-2×1=-3,∴g[f(1)]=g(-3)=-3+1=-2.(2)令f(x)=t,则原方程化为g(t)=a,易知方程f(x)=t在t∈(-∞,1)内有2个不同的解,则原方程有4个解等价于函数y=g(t)(t<1)与y=a的图象有2个不同的交点,作出函数y=g(t)(t<1)的图象,如图所示,由图象可知,当1≤a<时,函数y=g(t)(t<1)与y=a有2个不同的交点,即所求a的取值范围是.
16.(2019·德州模拟)已知函数f(x)=-x2-2x.g(x)=(1)求g[f(1)]的值;(2)若方程g[f(x)]-a=0有4个实数根,求实数a的取值范围.解:(1)∵f(1)=-12-2×1=-3,∴g[f(1)]=g(-3)=-3+1=-2.(2)令f(x)=t,则原方程化为g(t)=a,易知方程f(x)=t在t∈(-∞,1)内有2个不同的解,则原方程有4个解等价于函数y=g(t)(t<1)与y=a的图象有2个不同的交点,作出函数y=g(t)(t<1)的图象,如图所示,由图象可知,当1≤a<时,函数y=g(t)(t<1)与y=a有2个不同的交点,即所求a的取值范围是. 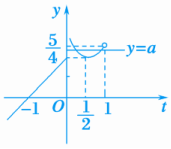
相关试卷
这是一份高考数学一轮复习课时作业:1 集合 Word版含解析,共7页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
这是一份(艺术生)高考数学一轮复习讲与练:考点11 函数与方程 (含解析),共8页。试卷主要包含了函数的零点,函数零点存在性定理,二分法,二分法求函数f零点近似值的步骤,故选D.,函数的零点为________等内容,欢迎下载使用。
这是一份高考数学(理数)一轮复习课时作业11《函数与方程》(原卷版),共3页。









