


所属成套资源:高考数学一轮复习课时作业 含解析
高考数学一轮复习课时作业:30 数系的扩充与复数的引入 Word版含解析
展开
这是一份高考数学一轮复习课时作业:30 数系的扩充与复数的引入 Word版含解析,共6页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
![]() 课时作业30 数系的扩充与复数的引入
课时作业30 数系的扩充与复数的引入![]() 一、选择题1.若集合A={i,i2,i3,i4}(i是虚数单位),B={1,-1},则A∩B等于( C )A.{-1} B.{1}C.{1,-1} D.∅解析:因为A={i,i2,i3,i4}={i,-1,-i,1},B={1,-1},所以A∩B={-1,1}.2.已知i是虚数单位,复数z满足-=,则|z|=( A )A.1 B.C. D.2解析:因为=,即=,即=-i,故(1-i)z=-1-i,所以z=-=-=-i,则|z|=1,应选A.3.已知复数z=|(-i)i|+i5(i为虚数单位),则复数z的共轭复数为( A )A.2-i B.2+iC.4-i D.4+i解析:由题意知z=|i+1|+i=+i=2+i,则=2-i.4.设复数z满足i(z+1)=-3+2i(i是虚数单位),则复数z对应的点位于复平面内( A )A.第一象限 B.第二象限C.第三象限 D.第四象限解析:由i(z+1)=-3+2i,得z=-1=-1=2+3i-1=1+3i,它在复平面内对应的点为(1,3),位于第一象限.5.已知i为虚数单位,若复数z=(a∈R)的虚部为-3,则|z|=( C )A. B.2C. D.5解析:因为z====-i,所以-=-3,解得a=5,所以z=-2-3i,所以|z|==.6.若复数m(3+i)-(2+i)在复平面内对应的点位于第四象限,则实数m的取值范围为( D )A.m>1 B.m>C.m<或m>1 D.<m<1解析:m(3+i)-(2+i)=(3m-2)+(m-1)i由题意,得解得<m<1.7.若复数z=a2-1+(a+1)i(a∈R)是纯虚数,则的虚部为( A )A.- B.-iC. D.i解析:由题意得所以a=1,所以===-i,根据虚部的概念,可得的虚部为-.8.已知复数z=1+,则1+z+z2+…+z2 015=( D )A.1+i B.1-iC.i D.0解析:z=1+=1+=i,∴1+z+z2+…+z2 015====0.二、填空题9.(2018·天津卷)i是虚数单位,复数=4-i.解析:===4-i.10.若复数z满足i·z=1+2i,其中i是虚数单位,则z的实部为2.解析:复数z==(1+2i)(-i)=2-i的实部是2.11.已知=b+i(a,b∈R),其中i为虚数单位,则a+b=1.解析:因为=b+i,所以2-ai=b+i.由复数相等的充要条件得b=2,a=-1.故a+b=1.12.在复平面上,复数对应的点到原点的距离为.解析:解法1:由题意可知==.解法2:=====+i,===.
一、选择题1.若集合A={i,i2,i3,i4}(i是虚数单位),B={1,-1},则A∩B等于( C )A.{-1} B.{1}C.{1,-1} D.∅解析:因为A={i,i2,i3,i4}={i,-1,-i,1},B={1,-1},所以A∩B={-1,1}.2.已知i是虚数单位,复数z满足-=,则|z|=( A )A.1 B.C. D.2解析:因为=,即=,即=-i,故(1-i)z=-1-i,所以z=-=-=-i,则|z|=1,应选A.3.已知复数z=|(-i)i|+i5(i为虚数单位),则复数z的共轭复数为( A )A.2-i B.2+iC.4-i D.4+i解析:由题意知z=|i+1|+i=+i=2+i,则=2-i.4.设复数z满足i(z+1)=-3+2i(i是虚数单位),则复数z对应的点位于复平面内( A )A.第一象限 B.第二象限C.第三象限 D.第四象限解析:由i(z+1)=-3+2i,得z=-1=-1=2+3i-1=1+3i,它在复平面内对应的点为(1,3),位于第一象限.5.已知i为虚数单位,若复数z=(a∈R)的虚部为-3,则|z|=( C )A. B.2C. D.5解析:因为z====-i,所以-=-3,解得a=5,所以z=-2-3i,所以|z|==.6.若复数m(3+i)-(2+i)在复平面内对应的点位于第四象限,则实数m的取值范围为( D )A.m>1 B.m>C.m<或m>1 D.<m<1解析:m(3+i)-(2+i)=(3m-2)+(m-1)i由题意,得解得<m<1.7.若复数z=a2-1+(a+1)i(a∈R)是纯虚数,则的虚部为( A )A.- B.-iC. D.i解析:由题意得所以a=1,所以===-i,根据虚部的概念,可得的虚部为-.8.已知复数z=1+,则1+z+z2+…+z2 015=( D )A.1+i B.1-iC.i D.0解析:z=1+=1+=i,∴1+z+z2+…+z2 015====0.二、填空题9.(2018·天津卷)i是虚数单位,复数=4-i.解析:===4-i.10.若复数z满足i·z=1+2i,其中i是虚数单位,则z的实部为2.解析:复数z==(1+2i)(-i)=2-i的实部是2.11.已知=b+i(a,b∈R),其中i为虚数单位,则a+b=1.解析:因为=b+i,所以2-ai=b+i.由复数相等的充要条件得b=2,a=-1.故a+b=1.12.在复平面上,复数对应的点到原点的距离为.解析:解法1:由题意可知==.解法2:=====+i,===.![]() 13.如图所示的网格纸中小正方形的边长是1,复平面内点Z对应的复数z满足(z1-i)·z=1,则复数z1=( B )
13.如图所示的网格纸中小正方形的边长是1,复平面内点Z对应的复数z满足(z1-i)·z=1,则复数z1=( B )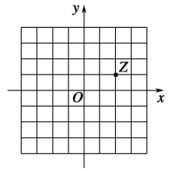 A.-+i B.+iC.-i D.--i解析:由题意得z=2+i, 所以z1=+i=+i=+i.14.(2019·枣庄模拟)已知m为实数,i为虚数单位,若m+(m2-4)i>0,则=i.解析:因为m+(m2-4)i>0,所以⇒m=2,故==i. 15.(2019·江西南昌一模)欧拉公式eix=cosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发现的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”.根据欧拉公式可知,e表示的复数位于复平面中的( A )A.第一象限 B.第二象限C.第三象限 D.第四象限解析:由题意可得e=cos+isin=+i,即e表示的复数位于复平面中的第一象限.故选A.16.(2019·福州四校联考)已知复数z=x+yi(x,y∈R)满足||≤1,则y≥x+1的概率为( B )A.- B.-C.+ D.+解析:复数z=x+yi(x,y∈R),||≤1,它的几何意义是以O(0,0)为圆心,1为半径的圆以及内部部分.满足y≥x+1的图象如图中圆内阴影部分所示.则概率P==-.
A.-+i B.+iC.-i D.--i解析:由题意得z=2+i, 所以z1=+i=+i=+i.14.(2019·枣庄模拟)已知m为实数,i为虚数单位,若m+(m2-4)i>0,则=i.解析:因为m+(m2-4)i>0,所以⇒m=2,故==i. 15.(2019·江西南昌一模)欧拉公式eix=cosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发现的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”.根据欧拉公式可知,e表示的复数位于复平面中的( A )A.第一象限 B.第二象限C.第三象限 D.第四象限解析:由题意可得e=cos+isin=+i,即e表示的复数位于复平面中的第一象限.故选A.16.(2019·福州四校联考)已知复数z=x+yi(x,y∈R)满足||≤1,则y≥x+1的概率为( B )A.- B.-C.+ D.+解析:复数z=x+yi(x,y∈R),||≤1,它的几何意义是以O(0,0)为圆心,1为半径的圆以及内部部分.满足y≥x+1的图象如图中圆内阴影部分所示.则概率P==-.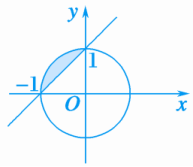
相关试卷
这是一份高考数学一轮复习课时训练:第6章 数 列 30 Word版含解析(含答案),共6页。
这是一份高考数学一轮复习课时作业:53 双曲线 Word版含解析,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高考数学一轮复习课时作业:50 圆的方程 Word版含解析,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








